IEEE浮点标准:V=(-1)^s*M*2^E
1.符号(sign)s决定这个数是负数(s=1)还是正数,0(s=0)。
2.尾数(significand) M是一个二进制小数.
3.阶码(exponent)E对浮点数加权。
单精度,双精度的表示如下:
exp为阶码,frac为尾数

给定了位表示,根据exp的值,被编码的值可以分为三种情况:
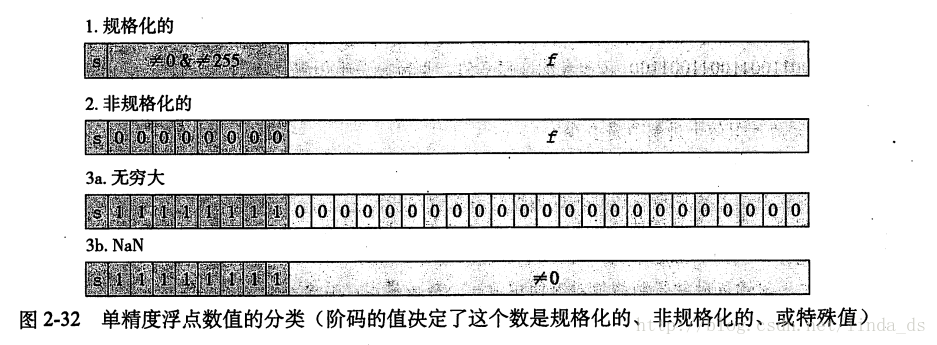
规格化的表示一般的数,非规格化的表示靠近0的数或0,阶码都为1的,当尾数为0时表示无穷大(即溢出),阶码都为1的,当尾数不为0时表示不存在的数,例如-1开根号之类的。
规格化的数阶码字段被解释为以偏置(biased)形式表示的有符号整数。其实就是一个无符号数e,在进行运算时将E=e-Bias,Bias为偏移量(2^(k-1)-1)。小数字段frac表示为0<frac<1,小数点前的1默认存在不写,尾数M=1+frac。
非规格化的数,阶码全为0,阶码值为E=1-Bias,这是为了让数从非规格化的数到规格化的数(开始也为1-Bias)时能平滑转换。
无穷大,阶码全1,小数全0。s=0时,表示正无穷,s=1时,表示负无穷。也可表示溢出,两个数很大相乘时,或除以0时。
NaN,阶码全1,小数非0时。一些运算结果不是实数或无穷就返回NaN,也可表示未初始化的数据。
例子
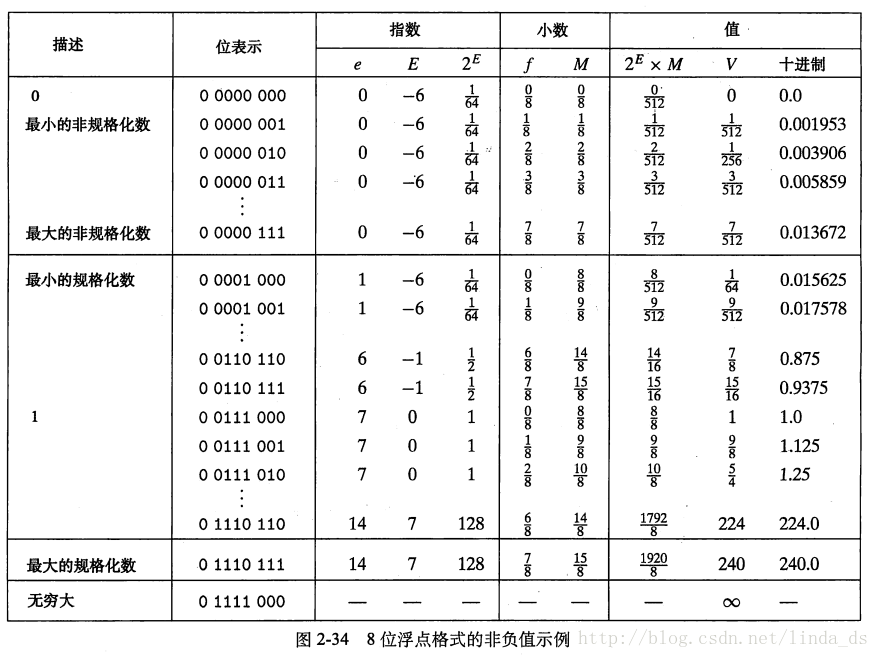
很有趣的现象,将正浮点数的位级表达解释为无符号整数,它们是按升序排列的,负浮点数则为降序。
舍入
舍入包括四种:向上舍入,向下舍入,向0舍入,向偶数舍入。
1.向上舍入是指每次舍入都进位,如1.4->2,1.5->2,-1.4 -> -1;
2.向下舍入是指每次舍入都向下舍入,如1.4->1,1.5->1,-1.5->-2;
3.向0舍入是指正负数都向0方向舍入,如1.4->1,1.5->1,-1.5->-1;
4.向偶数舍入指向上或者向下舍入,尽量使结果的最低有效数字为偶数,也就是向最靠近的数舍入,如1.5->2,1.4->1,2.5->2,-1.5->-2。
向偶数舍入有一点比较难理解:
**数字最低位有效位为偶数时就不用考虑低位进位了吗?
其实不然,如1.2453000精确到百分位,用向偶数舍入得到1.25。也就是说当某个数不是可能精确值的中间值时,优先考虑低位进位情况,在这个例子中1.24、1.25为可能的精确值,1.2453000显然不是这两个数的中间值,所以优先考虑后面的进位情况。当这个数为中间值时,优先考虑最低位有效位是否为偶数,是则舍去后面的,如1.245000->1.24,不是则考虑低位进位,如1.235000->1.24。
向偶数舍入也被用于浮点数中,二进制的0为偶数,1为奇数。道理和上面一致。非中间值,考虑低位进位,如10.00110->10.01(保留2位小数),中间值,考虑最低位有效位,如10.10100->10.10(保留2位小数)
浮点运算
浮点加法
IEEE规定,1/-0将产生负无穷大,1/+0将产生正无穷大。
实数的加法也形成了阿贝尔群,但我们必须考虑舍入对这些属性的影响。x + y= y+x,这个运算是可交换的,但不可结合的。如,(3.14+1e10)求值为0.0——因为舍入,值3.14丢失了。而3.14+(1e10-1e10)为3.14。
作为阿贝尔群,大多数浮点数都是有逆元的,但无穷和NaN是除外的,正无穷+负无穷=NaN,NaN+x=NaN。
此外,浮点加法满足单调性属性:如果a>=b,那么对于任意a,b以及x,除了NaN(个人感觉无穷也应该除外),都有x+a>=x+b。无符号或补码加法不具有该属性。
浮点乘法
浮点乘法遵循通常乘法的所具有的许多特性。浮点乘法是封闭的(即使可能产生无穷大和NaN),它也是可交换的,并且它的乘法单位元为1.0。不具备可结合性,如在单精度浮点下,(1e20*1e20)le-20为正无穷大,而1e20(1e20*1e-20)为1e20。此外,浮点乘法在加法上不具备分配性,如在单精度浮点数下,1e20*(1e20-1e20)为0.0,而1e20*1e20-1e20*1e20为NaN。
此外,对于任何a,b和c,并且a,b,c都不等于NaN,浮点乘法满足下列单调性: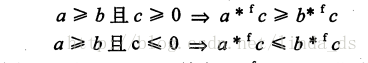
只要a不等于NaN,就有a*a>=0。
无符号或补码的乘法没有这些单调性。