浮点数不精确的原因 以及 IEEE754浮点数的表示方法

浮点数为什么不精确？

其实这句话本身就不精确， 相对精确一点的说法是： 我们码农在程序里写的10进制小数，计算机内部无法用二进制的小数来精确的表达。

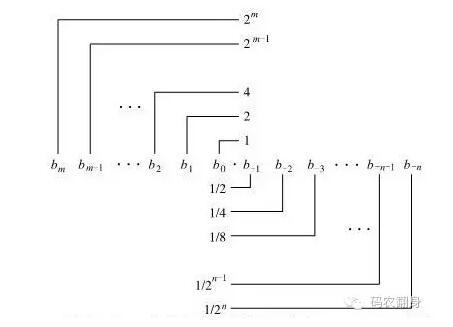
什么是二进制的小数？ 就是形如 101.11 数字，注意，这是二进制的，数字只能是0和1。

101.11 就等于 1 * 2^2 +0 *2^1 + 1*2^0 + 1*2^-1 + 1*2^-2 = 4+0+1+1/2+1/4 = 5.75

下面的图展示了一个二进制小数的表达形式。

从图中可以看到，对于二进制小数，小数点右边能表达的值是 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128 … 1/(2^n）

现在问题来了， 计算机只能用这些个 1/(2^n） 之和来表达十进制的小数。

我们来试一试如何表达十进制的 0.2 吧。

0.01 = 1/4 = 0.25 ,太大

0.001 =1/8 = 0.125 , 又太小

0.0011 = 1/8 + 1/16 = 0.1875 , 逼近0.2了

0.00111 = 1/8 + 1/16 + 1/32 = 0.21875 , 又大了

0.001101 = 1/8+ 1/16 + 1/64 = 0.203125 还是大

0.0011001 = 1/8 + 1/16 + 1/128 = 0.1953125 这结果不错

0.00110011 = 1/8+1/16+1/128+1/256 = 0.19921875 
已经很逼近了， 就这样吧。

这就是我说的用二进制小数没法精确表达10进制小数的含义。

浮点数的计算机表示

那计算机内部具体是怎么表示的呢？

计算机不可能提供无限的空间让程序去存储这些二进制小数。

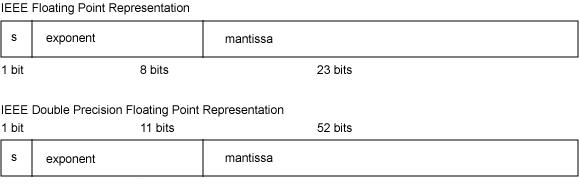
它需要规定长度， 在Java 中， 提供了两种方式： float 和double ， 分别是32位和64位。

可以这样查看一下一个float的内部表示（以0.09f为例）： 
Float.floatToRawIntBits(0.09f)

你将会得到：1035489772， 这是10进制的， 转化成二进制， 在前面加几个0补足 32位就是：

0 01111011 01110000101000111101100

你可以看到它分成了3段： 
第一段代表了符号(s) : 0 正数， 1 负数 ， 其实更准确的表达是 (-1) ^0

第二段是阶码(e)：01111011 　，对应的10进制是　123

第三段是尾数(M)

你看到了尾数和阶码，就会明白这其实是所谓的科学计数法: 
(-1)^s * M * 2^e

对于0.09f 的例子，就是： 
0101110000101000111101100 * (2^123) 
好像不对，这肯定远远大于0.09f !

这是因为浮点数遵循的是IEEE754 表示法， 我们刚才的s(符号) 是对的，但是 e(阶码)和 M（尾数）需要变换：

对于阶码e ， 一共有8位， 这是个有符号数， 特别是按照IEEE754 规范， 如果不是0或者255， 那就需要减去一个叫偏置量的值，对于float 是127

所以 E = e - 127 = 123-127 = -4

对于尾数M ，如果阶码不是0或者255， 他其实隐藏了一个小数点左边的一个 1 （节省空间，充分压榨每一个bit啊）。 
即 M = 1.01110000101000111101100

现在写出来就是: 
1.01110000101000111101100 * 2^-4 
=0.000101110000101000111101100 
= 1/16 + 1/64 + 1/128+ 1/256 + …. 
= 0.0900000035762786865234375

你看这就是0.09的内部表示， 很明显他比0.09更大一些， 是不精确的！

64位的双精度浮点数double是也是类似的， 只是尾数和阶码更长， 能表达的范围更大。 
符号位 ：1位 
阶码 ： 11位 
尾数： 52位

上面的例子0.09f 其实是所谓的规格化的浮点数， 还有非规格化的浮点数，这里就不展开了。

使用浮点数

由于浮点数表示的这种“不精确性”或者说是“近似性”， 对于精确度要求不高的运算还行， 如果我们用float或者double 来做哪些要求精确的运算（例如银行）时就要小心了, 很可能得不到你想要的结果。

具体的改进方法推荐大家看看《Effective Java》在第48条所推荐的“使用BigDecimal来做精确运算”。

1.浮点数的存储格式

浮点数在C/C++中对应float和double类型，我们有必要知道浮点数在计算机中实际存储的内容。

IEEE754标准中规定float单精度浮点数在机器中表示用 1 位表示数字的符号，用 8 位来表示指数，用23 位来表示尾数，即小数部分。对于double双精度浮点数，用 1 位表示符号，用 11 位表示指数，52 位表示尾数，其中指数域称为阶码。IEEE 浮点值的格式如下图所示。

注意，IEE754规定浮点数阶码E采用”指数ｅ的移码-1”来表示，请记住这一点。为什么指数移码要减去1，这是IEEE754对阶码的特殊要求，以满足特殊情况，比如对正无穷的表示。

2.浮点数的规格化

若不对浮点数的表示作出明确的规定，同一个浮点数的表示就不是唯一的。例如(1.75)10(1.75)10可以表示成1.11×201.11×20，0.111×210.111×21，0.0111×220.0111×22等多种形式。当尾数不为0时，尾数域的最高有效位为1，这称为浮点数的规格化。否则，以修改阶码同时左右移动小数点位置的办法，使其成为规格化数的形式。

2.1单精度浮点数真值

IEEE754标准中，一个规格化32位的浮点数x的真值表示为： 

x=(−1)S×(1.M)×2ex=(−1)S×(1.M)×2e

e=E−127e=E−127

其中尾数域表示的值是1.M。因为规格化的浮点数的尾数域最左位总是1，故这一位不予存储，而认为隐藏在小数点的左边。

在计算指数e时，对阶码E的计算采用源码的计算方式，因此32位浮点数的8bits的阶码E的取值范围是0到255。其中当E为全0或者全1时，是IEEE754规定的特殊情况，下文会另外说明。

2.2双精度浮点数真值

64位的浮点数中符号为1位，阶码域为11位，尾数域为52位，指数偏移值是1023。因此规格化的64位浮点数x的真值是： 

x=(−1)S×(1.M)×2ex=(−1)S×(1.M)×2e

e=E−1023e=E−1023

3.移码

移码（又叫增码）是对真值补码的符号位取反，一般用作浮点数的阶码，引入的目的是便于浮点数运算时的对阶操作。

对于定点整数，计算机一般采用补码的来存储。正整数的符号位为0，反码和补码等同于源码。

负整数符号位都固定为1，源码，反码和补码的表示都不相同，由原码表示法变成反码和补码有如下规则： 
（1）源码符号位为1不变，整数的每一位二进制数位求反得反码； 
（2）反码符号位为1不变，反码数值位最低位加1得补码。

比如，以一个字节8bits来表示-3，那么[−3]原=10000011[−3]原=10000011，[−3]反=11111100[−3]反=11111100，[−3]补=11111101[−3]补=11111101，那么-3的移码就是[−3]移=01111101[−3]移=01111101。

如何将移码转换为真值-3呢？先将移码转换为补码，再求值。

4.浮点数的具体表示

4.1十进制到机器码

（1）0.5 
0.5=(0.1)20.5=(0.1)2，符号位S为0，指数为e=−1e=−1，规格化后尾数为1.0。

单精度浮点数尾数域共23位，右侧以0补全，尾数域： 

M=[000 0000 0000 0000 0000 0000]2M=[000 0000 0000 0000 0000 0000]2

阶码E: 

E=[−1]移−1=[0111 1111]2−1=[0111 1110]2E=[−1]移−1=[0111 1111]2−1=[0111 1110]2

对照单精度浮点数的存储格式，将符号位S，阶码E和尾数域M存放到指定位置，得0.5的机器码： 

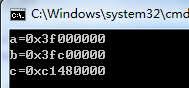
0.5=[0011 1111 0000 0000 0000 0000 0000 0000]20.5=[0011 1111 0000 0000 0000 0000 0000 0000]2

。

十六进制表示为0.5=0x3f000000。

（2）1.5 
1.5=[1.1]21.5=[1.1]2，符号位为0，指数e=0e=0，规格化后尾数为1.1。

尾数域Ｍ右侧以0补全，得尾数域: 

M=[100 0000 0000 0000 0000 0000]2M=[100 0000 0000 0000 0000 0000]2

阶码E： 

E=[０]移−1=[10000000]2−1=[01111111]2E=[０]移−1=[10000000]2−1=[01111111]2

得1.5的机器码： 

1.5=[0011 1111 1100 0000 0000 0000 0000 0000]21.5=[0011 1111 1100 0000 0000 0000 0000 0000]2

十六进制表示为1.5=0x3fc00000。

（3）-12.5 
−12.5=[−1100.1]2−12.5=[−1100.1]2，符号位S为1，指数e为3，规格化后尾数为1.1001，

尾数域Ｍ右侧以0补全，得尾数域: 

M=[100 1000 0000 0000 0000 0000]2M=[100 1000 0000 0000 0000 0000]2

阶码E： 

E=[3]移−1=[1000 0011]2−1=[1000 0010]2E=[3]移−1=[1000 0011]2−1=[1000 0010]2

即-12.5的机器码： 

−12.5=[1100 0001 0100 1000 0000 0000 0000 0000]2−12.5=[1100 0001 0100 1000 0000 0000 0000 0000]2

十六进制表示为-12.5=0xc1480000。

用如下程序验证上面的推算，代码编译运行平台Win32+VC++ 2012：

#include <iostream>
using namespace std;

int main(){
    float a=0.5;
    float b=1.5;
    float c=-12.5;

    unsigned int* pa=NULL;
    pa=(unsigned int*)&a;
    unsigned int* pb=NULL;
    pb=(unsigned int*)&b;
    unsigned int* pc=NULL;
    pc=(unsigned int*)&c;

    cout<<hex<<"a=0x"<<*pa<<endl;
    cout<<hex<<"b=0x"<<*pb<<endl;
    cout<<hex<<"c=0x"<<*pc<<endl;

    return 0;
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21

输出结果： 

验证正确。

4.2机器码到十进制

（1）若浮点数x的IEEE754标准存储格式为0x41360000，那么其浮点数的十进制数值的推演过程如下：

0x41360000=[0 10000010 011 0110 0000 0000 0000 0000]0x41360000=[0 10000010 011 0110 0000 0000 0000 0000]

根据该浮点数的机器码得到符号位S=0，指数e=阶码-127=1000 0010-127=130-127=3。

注意，根据阶码求指数时，可以像上面直接通过 “阶码-127”求得指数e，也可以将阶码+1=移码阶码+1=移码，再通过移码求其真值便是指数e。比如上面阶码10000010+1=10000011[移码]=>00000011[补]=3（指数e）10000010+1=10000011[移码]=>00000011[补]=3（指数e）。

包括尾数域最左边的隐藏位1，那么尾数1.M=1.011 0110 0000 0000 0000 0000=1.011011。

于是有： 

x=(−1)S×1.M×2e=+(1.011011)×23=+1011.011=(11.375)10x=(−1)S×1.M×2e=+(1.011011)×23=+1011.011=(11.375)10

通过代码同样可以验证上面的推算：

#include <iostream>
using namespace std;

int main(){
    unsigned int hex=0x41360000;
    float* fp=(float*)&hex;
    cout<<"x="<<*fp<<endl;
    return 0;
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

输出结果： 
 
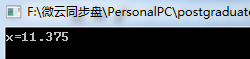
验证正确。

5.浮点数的几种特殊情况

（1）0的表示 
对于阶码为0或255的情况，IEEE754标准有特别的规定： 
如果 阶码E=0并且尾数M是0，则这个数的真值为±0（正负号和数符位有关）。

因此+0的机器码为：0 00000000 000 0000 0000 0000 0000。 
-0的机器码为：1 00000000 000 0000 0000 0000 0000。

需要注意一点，浮点数不能精确表示0，而是以很小的数来近似表示0。因为浮点数的真值等于（以32bits单精度浮点数为例）： 

x=(−1)S×(1.M)×2ex=(−1)S×(1.M)×2e

e=E−127e=E−127

那么+0的机器码对应的真值为 1.0×2−1271.0×2−127 。同理，-0机器码真值为 −1.0×2−127−1.0×2−127 。

（2）+∞+∞和−∞−∞的表示 
如果阶码E=255 并且尾数M全是0，则这个数的真值为±∞（同样和符号位有关）。因此+∞的机器码为：0 11111111 000 0000 0000 0000 0000。-∞的机器吗为：1 11111111 000 0000 0000 0000 0000。

（3）NaN（Not a Number） 
如果 E = 255 并且 M 不是0，则这不是一个数（NaN）。

6.浮点数的精度和数值范围

6.1浮点数的数值范围

根据上面的探讨，浮点数可以表示-∞到+∞，这只是一种特殊情况，显然不是我们想要的数值范围。

以32位单精度浮点数为例，阶码E由8位表示，取值范围为0-255，去除0和255这两种特殊情况，那么指数e的取值范围就是1-127=-126到254-127=127。

（1）最大正数 
因此单精度浮点数最大正数值的符号位S=0，阶码E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为：0 11111110 111 1111 1111 1111 1111 1111。

那么最大正数值: 

PosMax=(−1)S×1.M×2e=+(1.11111111111111111111111)×2127≈3.402823e+38PosMax=(−1)S×1.M×2e=+(1.11111111111111111111111)×2127≈3.402823e+38

这是一个很大的数。

（2）最小正数 
最小正数符号位S=0，阶码E=1，指数e=1-127=-126，尾数M=0，其机器码为0 00000001 000 0000 0000 0000 0000 0000。

那么最小正数为： 

PosMin=(−1)S×1.M×2e=+(1.0)×2−126≈1.175494e−38PosMin=(−1)S×1.M×2e=+(1.0)×2−126≈1.175494e−38

这是一个相当小的数。几乎可以近似等于0。当阶码E=0，指数为-127时，IEEE754就是这么规定1.0×2−1271.0×2−127近似为0的，事实上，它并不等于0。

（3）最大负数 
最大负数符号位S=1，阶码E=1，指数e=1-127==-126，尾数M=0，机器码与最小正数的符号位相反，其他均相同，为：1 00000001 000 0000 0000 0000 0000 0000。

最大负数等于： 

NegMax=(−1)S×1.M×2e=−(1.0)×2−126≈−1.175494e−38NegMax=(−1)S×1.M×2e=−(1.0)×2−126≈−1.175494e−38

（4）最小负数 
符号位S=0，阶码E=254，指数e=254-127=127，尾数M=111 1111 1111 1111 1111 1111，其机器码为：1 11111110 111 1111 1111 1111 1111 1111。

计算得： 

NegMin=(−1)S×1.M×2e=+(1.11111111111111111111111)×2127=−3.402823e+38NegMin=(−1)S×1.M×2e=+(1.11111111111111111111111)×2127=−3.402823e+38

6.2浮点数的精度

说道浮点数的精度，先给精度下一个定义。浮点数的精度是指浮点数的小数位所能表达的位数。

阶码的二进制位数决定浮点数的表示范围，尾数的二进制位数表示浮点数的精度。以32位浮点数为例，尾数域有23位。那么浮点数以二进制表示的话精度是23位，23位所能表示的最大数是223−1=8388607223−1=8388607，所以十进制的尾数部分最大数值是8388607，也就是说尾数数值超过这个值，float将无法精确表示，所以float最多能表示小数点后7位，但绝对能保证的为6位，也即float的十进制的精度为为6~7位。

64位双精度浮点数的尾数域52位，因252−1=4,503,599,627,370,495252−1=4,503,599,627,370,495，所以双精度浮点数的十进制的精度最高为16位，绝对保证的为15位，所以double的十进制的精度为15~16位。。

7.小结

本文操之过急，但也花了将近一天的时间，难免出现编辑错误和不当说法，请网友批评指正。不明之处，欢迎留言交流。对浮点数的乘法、除法运算还未涉及，后续可能会去学习并记录学习所得，与大家分享。

转自http://blog.csdn.net/k346k346/article/details/50487127