欧几里得算法
1.引入
问题:求线段上格点的个数
给定平面两个格点P1=(x1,x2)和P2=(x2,y2),线段P1P2上,除P1,P2外还有几个格点。
格点:横纵左边均为整数的点。
答案:|x1-x2|与|y1-y2|的最大公约数-1(若点P1,P2重合,答案为0)
原因:
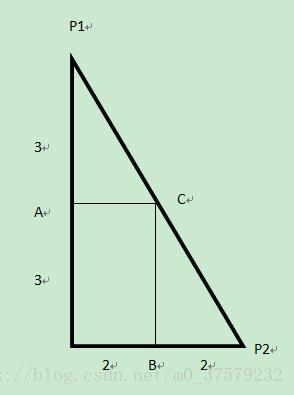
设d1 = |x1-x2|,d2 = |y1-y2|,d1=a*b,d2=b*c,b是二者的最大公约数,则以这两条线做一个直角三角形,纵边可以看成被分成b个a长的线段,横边可看成被分成b个c长的线段,如图
那么可以把斜边分成b个等长线段,因为A点,B点肯定是格点,xc=xb,yc=ya,所以C点肯定也是格点,又因为C点在线P1,P2上,所以C是P1P2上的格点。
因此可知:P1P2上格点数 = |x1-x2|与|y1-y2|的最大公约数-1(若点P1,P2重合,答案为0)
2.代码
gcd(a,b)=gcd(b,a%b),gcd(c,0)=c
因此,可构造递归函数,直到gcd函数的第二个参数值为0。
int gcd(int a,int b){
if(b==0)return a;
return gcd(b,a%b);
}扩展欧几里得算法
1.引入
问题:一个双六上面有向前和向后的无线延续的格子,每个格子都写有一个整数。0是起点,1是终点。而骰子上只有a,b,-a,-b四个整数,所以根据ab值得不同,有可能无法到达终点。
掷出四个整数各多少次可以到达终点?多解任意输出一组
数学表述就是:求任一一组x,y使得ax+by=1。
可以发现,如果gcd(a,b)!=1,则无解,反之可以通过扩展原来的辗转相除法来求解。事实上,一定存在整数对(x,y)使得ax+by=gcd(a,b)。
裴蜀定理:
- 对于任何整数a,b且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别的,一定存在整数x,y使得ax+by=d成立。
重要推论:
- a,b互质的充要条件是存在整数x,y使得ax+by=1。
2.推导
假设:未知ax+by=gcd(a,b)的解(x,y),已知bx1+(a%b)y1=gcd(b,a%b)的解(x1,y1)
ax+by=bx1+(a%b)y1
=bx1+(a-(a/b)*b)y1
=ay1+b(x1-(a/b)y1)
x=y1,y=x1-(a/b)y1
- 这里用假设我们知道递归下一步的解来构建递归方程,其实我们是不知道的,直到y=0,因为ax=gcd(a,0)=a,求得x=1,到达了递归的终点,我们再向上推,求出原方程的解。
- 事实上,如果ab!=0,可以知道求出的|x|<=b,|y|<=a。
3.代码
int extgcd(int a,int b,int& x,int& y){//返回值是a,b的最大公约数
int d=a;
if(b!=0){
d=extgcd(b,a%b,x,y);
int x1=x,y1=y;
x=y1;
y=x1-(a/b)*y1;
}
else{
x=1;y=0;
}
return d;
}也可以写成:
int extgcd(int a,int b,int& x,int& y){//返回值是a,b的最大公约数
int d=a;
if(b!=0){
d=extgcd(b,a%b,y,x);
y-=(a/b)*x;
}
else{
x=1;y=0;
}
return d;
}4.复杂度
gcd和extgcd复杂度是相同的。O(log max(a,b))