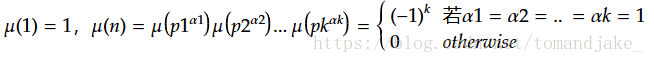莫比乌斯反演完全入门讲解

莫比乌斯反演实际上是一两个公式定理的运用，自认为想要掌握它的话，其中的证明还是有必要了解的。看过网上一些博客，感觉都只证明了一半，没看到有人将这个定理完全证明出来。然而我最近在正好在学习初等数论，发现完全证明这个定理实际上并不需要很多知识，特此填坑。另外加上一些应用以构成完整的讲解。

实际上，这个定理的证明用到了一点数论函数相关知识。前置技能在此Mathcha传送门

内容并不多，自认为把这一页笔记内容学会，自己就可以把莫比乌斯反演的证明当练习题一样独立完成。接下来我还是会进行解释，当然，如果觉得我的解释不好，完全可以自己看这个笔记学习，我甚至都推荐自己看笔记，因为如果熟悉这样的数学语言的话，其实看的很快而且会有自己的认识。而且其中给出了欧拉函数的推导，没有学过欧拉函数的话，看这个也可以更加高效地学完这一块内容。(注意笔记中(m,n)=gcd(m,n) )

好，我们进入正题。首先，我们引入三个定义

Definition 1 可乘函数：算术函数f，满足只要gcd(m,n) =1,就有f(mn)=f(m)f(n)。

没错, 比其他可乘函数宽泛一点，只要在gcd(m,n)=1条件下满足可乘就行。然后我们知道由唯一分解定理，任何正整数n可分解为若干素数的幂方积 $n=p^{\alpha 1}_{1} p^{\alpha 2}_{2} .....p^{\alpha k}_{k}$ ,所以若 $\theta$ 为可乘函数，有

$\theta ( n) =\theta \left( p1^{\alpha 1}\right) \theta \left( p2^{\alpha 2}\right) ...\theta \left( pk^{\alpha k}\right)$ ..................................................................(1)

Definition 2 $\sum _{d|n}$ ：代表对n的所有正因子求和，如

$\sum _{d|4}d^2=1^2+2^2+4^2$

Definition 3 莫比乌斯函数：

定义有点奇怪，关于这个函数，之后我们可以看到它的作用, 必须提到的是，可以证明，莫比乌斯函数是可乘函数。

然后是我们的目标----莫比乌斯反演定理：

Theorem 1 莫比乌斯反演定理: F(n)和f(n)为算术函数，若他们满足

$F(n)=\sum_{d|n}f(d)$

则有

$f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})$

证明如下：

首先给出一个定理，

至于 $\sum_{d|n}\theta(d)$ 为可乘函数的证明，可参见我的笔记。

之后可以得到下一个定理

定理3证明：

可以看到，莫比乌斯反演提供了一个F(n)与f(n)的连接，而他们之间的桥梁就是莫比乌斯函数 $\mu$ 。之后我们会看到具体的例子。这里先给出线性筛莫比乌斯函数的代码：

int mu[maxn], vis[maxn];
int primes[maxn], cnt;
void get_mu() {
	memset(vis, 0, sizeof(vis));
	memset(mu, 0, sizeof(mu));
	cnt = 0; mu[1] = 1;
	for (int i = 2; i <= maxn; ++i) {
		if (!vis[i]) { primes[cnt++] = i; mu[i] = -1; }
		for (int j = 0; j<cnt&&primes[j] * i <= maxn; ++j) {
			vis[primes[j] * i] = 1;
			if (i%primes[j] == 0)break;
			mu[i*primes[j]] = -mu[i];
		}
	}
}

应用举例：POJ 3904

题目给出n和n个正整数，问能找出多少个不同的四元组(a,b,c,d)使得该四元组的最大公因数为1.

分析：

首先要提的是，我们做题目往往用的是莫比乌斯反演的另外一种形式：

既然要用到莫比乌斯反演，我们首先就要找到合适的F和f。实际上，F和f的关系在于整除。我们可以假设

F(n)为有多少个四元组满足gcd(a,b,c,d)=n的整数倍

f(n)为有多少个四元组满足gcd(a,b,c,d)=n

所以我们的目标就是求f(1), 而实际上可以看出F与f构成了一组莫比乌斯变换对。有了反演公式，我们可以通过求F来求f，而这里面F很好求，要求F（n）我们只要在原数组中数出到能被n整除的数的个数m, 则C（m,4）就是F（n）

而由公式，由此我们可以发现

直接计算即可。

代码：

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
#include<stack>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<sstream>
#include<cmath>
#include<iterator>
#include<bitset>
#include<stdio.h>
using namespace std;
#define _for(i,a,b) for(int i=(a);i<(b);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
typedef long long LL;
const int INF = 1 << 30;
const int MOD = 1e9 + 7;
const int maxn = 10005;

int n, a[maxn], tot[maxn];
int mu[maxn], vis[maxn];
int primes[maxn], cnt;
void get_mu() {
	memset(vis, 0, sizeof(vis));
	memset(mu, 0, sizeof(mu));
	cnt = 0; mu[1] = 1;
	for (int i = 2; i <= maxn; ++i) {
		if (!vis[i]) { primes[cnt++] = i; mu[i] = -1; }
		for (int j = 0; j<cnt&&primes[j] * i <= maxn; ++j) {
			vis[primes[j] * i] = 1;
			if (i%primes[j] == 0)break;
			mu[i*primes[j]] = -mu[i];
		}
	}
}

void get_tot() {
	memset(tot, 0, sizeof(tot));
	for (int i = 0; i<n; ++i) {
		int x = a[i];
		int m = sqrt(x);
		for (int j = 1; j <= m; ++j) {
			if (x%j == 0)tot[j]++, tot[x / j]++;
		}
		if (m*m == x)tot[m]--;
	}
}
LL Cn4(int m) {
	if (m == 0)return 0;
	return 1ll * m*(m - 1)*(m - 2)*(m - 3) / 24;
}
int main()
{
	//freopen("C:\\Users\\admin\\Desktop\\in.txt", "r", stdin);
	//freopen("C:\\Users\\admin\\Desktop\\out.txt", "w", stdout);
	get_mu();
	while (~scanf("%d", &n)) {
		for (int i = 0; i<n; ++i) scanf("%d", &a[i]);
		get_tot();
		LL ans = 0;
		for (int i = 1; i<maxn; ++i) {
			ans += 1ll * mu[i] * Cn4(tot[i]);
		}
		printf("%I64d\n", ans);
	}

	return 0;
}

这样莫比乌斯反演就算是入门了吧。

莫比乌斯反演完全入门讲解

猜你喜欢