前置知识点:click具体一些简单的证明可以自己证明一下。
具体的各项知识以及证明待更吧。。。。
题目:click
题意:给出a,b,c,d,k,求出a<=x<=b, c<=y<=d 且gcd(x,y) = k 的(x,y)的对数。 说明了(5,7)和(7,5)是同一对。可以把a,c看作是1。
思路:
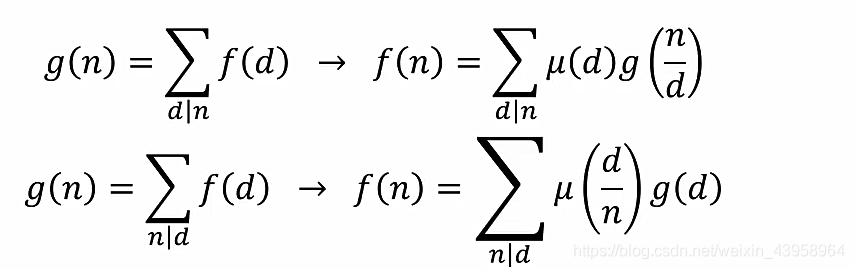 由上述公式,先进行分析,线性筛选求莫比乌斯函数可以直接看代码,也比较好理解。
由上述公式,先进行分析,线性筛选求莫比乌斯函数可以直接看代码,也比较好理解。
gcd(x,y)=k,那么gcd(x/k,y/k)=1,其实就是找[1,x/k]和[1,y/k]里面互质的对数,考虑到时间复杂度,只能继续化简。如果用欧拉函数的话,不能的确定x,y的范围也是不行的。
设
f(d):有多少对(x,y)满足gcd(x,y)=d
g(d):有多少对(x,y)满足gcd(x,y)=d的倍数。
构造完直接利用反演公式代入计算。
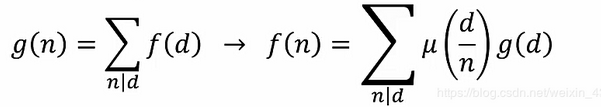 g(d)我们可以知道的是:g(d)=
。(n,m是范围,也就是x/k,y/k)
g(d)我们可以知道的是:g(d)=
。(n,m是范围,也就是x/k,y/k)
那么我们去计算f(1)即可获得答案。注意区间的端点是找相对小的那个(范围有大小限制,d最大就是min(b/k,d/k))以及(1,2)和(2,1)是相同的需要处理。
#include<cmath>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cstdlib>
#include<istream>
#include<vector>
#include<stack>
#include<set>
#include<map>
#include<algorithm>
#include<queue>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define MAX_len 200005*4
using namespace std;
typedef long long ll;
typedef pair<int,int> PP;
const int mod=998244353;
const int MAXlen=1e5+10;
long double eps=1e-9;
int prime[100100];
int tot=0;
int mu[100100];
bool vis[100100];
void init()
{
tot=0;
memset(mu,0,sizeof(mu));
memset(vis,false,sizeof(vis));
vis[0]=vis[1]=true;
mu[1]=1;
for(int i=2;i<MAXlen;i++)
{
if(!vis[i])
{
prime[tot++]=i;
mu[i]=-1;
}
for(int j=0;j<tot&&i*prime[j]<MAXlen;j++)
{
vis[i*prime[j]]=true;
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else
{
mu[i*prime[j]]=-mu[i];
}
}
}
}
int main()
{
init();
int T;
scanf("%d",&T);
int yy=1;
while(T--)
{
int a,b,c,d,k;
scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
if(!k)
{
printf("Case %d: 0\n",yy++);
continue;
}
ll ans=0;
b/=k;
d/=k;
int temp=min(d,b);
for(int i=1;i<=temp;i++)
{
ans+=ll(mu[i]*ll(b/i)*ll(d/i));
}
ll sum=0;
for(int i=1;i<=temp;i++)
{
sum+=ll(mu[i]*ll(temp/i)*ll(temp/i));
}
printf("Case %d: %lld\n",yy++,ans-sum/2);
}
return 0;
}