【代数学作业4】范数与迹
- 写在最前面
- 1. 极小多项式
-
- 1. 对 α \alpha α 的极小多项式
- 2. 对 α + 1 \alpha + 1 α+1 的极小多项式
- 3. 对 α 2 + α + 1 \alpha^2 + \alpha + 1 α2+α+1 的极小多项式
- 2. 范数 N N N
- 3. 数域 K K K 的范数 N K N_K NK
- 4. 迹 T T T
- 5. 数域 K K K 的迹 T K T_K TK
写在最前面

汇总版,省略了中间试错的过程与步骤
1. 极小多项式
1. 对 α \alpha α 的极小多项式
- 表达式变换:设 f ( x ) = x − α = x − 2 3 − − 2 f(x) = x - \alpha = x - \sqrt[3]{2} - \sqrt{-2} f(x)=x−α=x−32−−2。
- 消去根号:
-
首先处理 2 3 \sqrt[3]{2} 32:
-
然后处理 − 2 \sqrt{-2} −2,通过平方两边来消除根号:
-
因此, α \alpha α 的极小多项式为 f ( x ) = x 6 + 6 x 4 − 4 x 3 + 12 x 2 + 24 x + 12 f(x) = x^6 + 6x^4 - 4x^3 + 12x^2 + 24x + 12 f(x)=x6+6x4−4x3+12x2+24x+12。
-
和手动计算结果一致
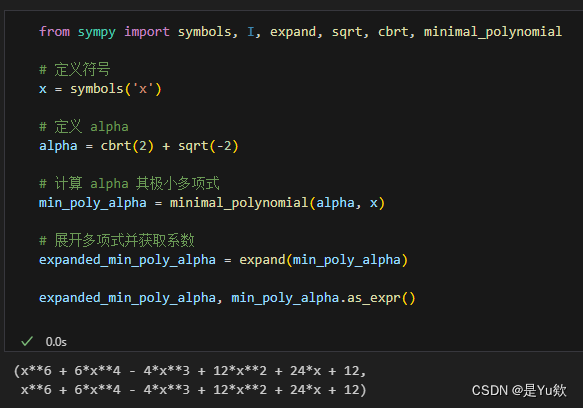
2. 对 α + 1 \alpha + 1 α+1 的极小多项式
α + 1 \alpha + 1 α+1 的极小多项式,该多项式是:
f ( x ) = x 6 − 6 x 5 + 21 x 4 − 48 x 3 + 75 x 2 − 42 x + 11 f(x) = x^6 - 6x^5 + 21x^4 - 48x^3 + 75x^2 - 42x + 11 f(x)=x6−6x5+21x4−48x3+75x2−42x+11
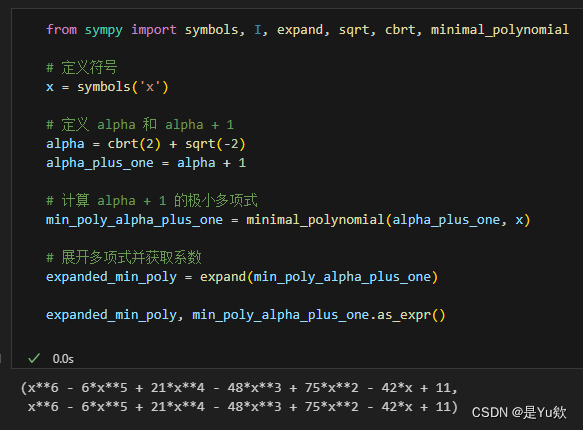
3. 对 α 2 + α + 1 \alpha^2 + \alpha + 1 α2+α+1 的极小多项式
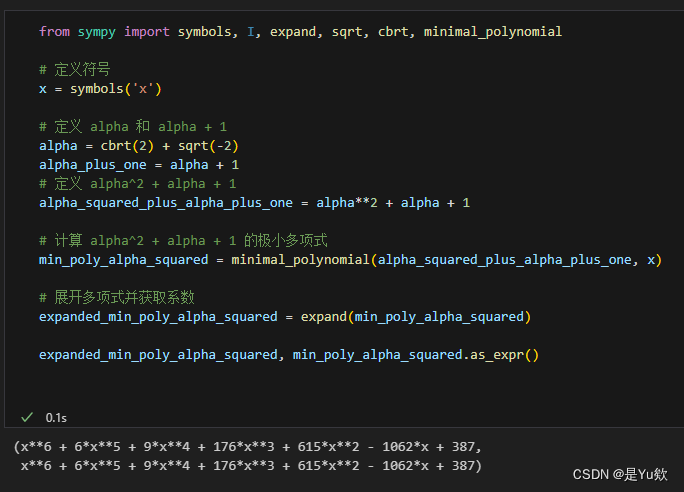
该多项式是: f ( x ) = x 6 + 6 x 5 + 9 x 4 + 176 x 3 + 615 x 2 − 1062 x + 387 f(x) = x^6 + 6x^5 + 9x^4 + 176x^3 + 615x^2 - 1062x + 387 f(x)=x6+6x5+9x4+176x3+615x2−1062x+387
2. 范数 N N N
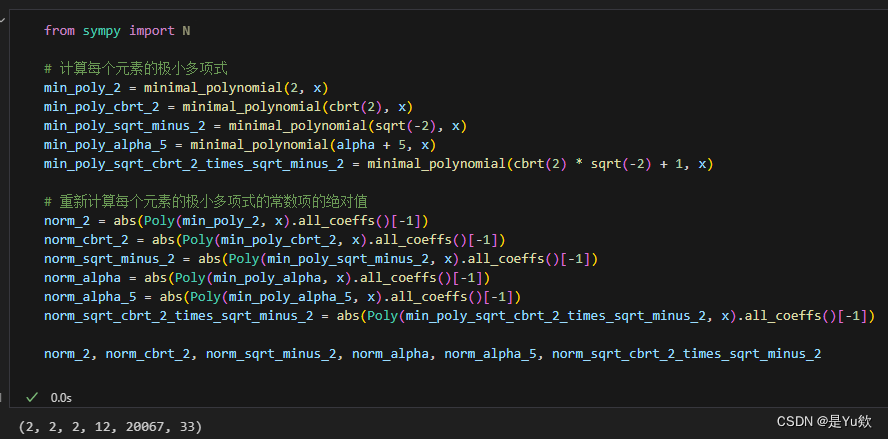
结果如下:
- N ( 2 ) N(2) N(2) 的范数为 2 2 2。
- N ( 2 3 ) N(\sqrt[3]{2}) N(32) 的范数为 2 2 2。
- N ( − 2 ) N(\sqrt{-2}) N(−2) 的范数为 2 2 2。
- N ( α ) N(\alpha) N(α) (其中 α = 2 3 + − 2 \alpha = \sqrt[3]{2} + \sqrt{-2} α=32+−2)的范数为 12 12 12。
- N ( α + 5 ) N(\alpha + 5) N(α+5) 的范数为 20067 20067 20067。
- N ( 2 3 − 2 + 1 ) N(\sqrt[3]{2}\sqrt{-2}+1) N(32−2+1) 的范数为 33 33 33。
3. 数域 K K K 的范数 N K N_K NK
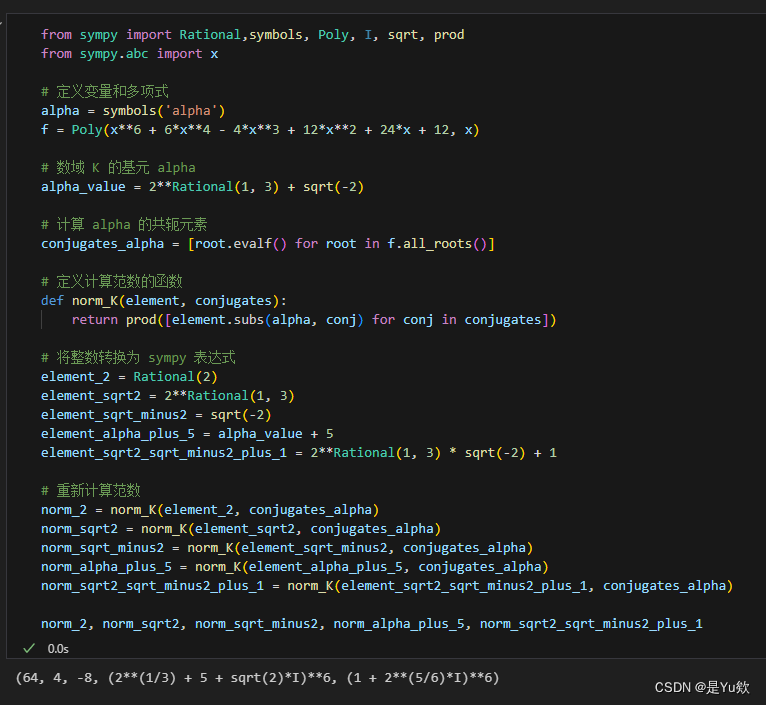
-
N K ( 2 ) N_K(2) NK(2)
2 2 2 是一个有理数,其最小多项式是 x − 2 x - 2 x−2。因此, N K ( 2 ) N_K(2) NK(2) 是这个多项式的根 2 2 2 的乘积,即 2 6 = 64 2^6 = 64 26=64(因为 α \alpha α 的最小多项式是六次的)。 -
N K ( 2 3 ) N_K(\sqrt[3]{2}) NK(32)
2 3 \sqrt[3]{2} 32 的共轭在 K K K 中有三个(因为它的最小多项式是三次的),包括 2 3 \sqrt[3]{2} 32, 2 3 ω \sqrt[3]{2}\omega 32ω, 和 2 3 ω 2 \sqrt[3]{2}\omega^2 32ω2(其中 ω \omega ω 是三次单位根)。在 K K K 中,我们需要考虑六个共轭,所以 N K ( 2 3 ) = ( 2 3 ) 3 × ( 2 3 ) 3 = 2 2 = 4 N_K(\sqrt[3]{2}) = (\sqrt[3]{2})^3 \times (\sqrt[3]{2})^3 = 2^2 = 4 NK(32)=(32)3×(32)3=22=4。 -
N K ( − 2 ) N_K(\sqrt{-2}) NK(−2)
− 2 \sqrt{-2} −2 的共轭在 K K K 中有两个(因为它的最小多项式是二次的),包括 − 2 \sqrt{-2} −2 和 − − 2 -\sqrt{-2} −−2。在 K K K 中,我们需要考虑六个共轭,所以 N K ( − 2 ) = ( − 2 ) 2 × ( − 2 ) 2 × ( − 2 ) 2 = ( − 2 ) 3 = − 8 N_K(\sqrt{-2}) = (\sqrt{-2})^2 \times (\sqrt{-2})^2 \times (\sqrt{-2})^2 = (-2)^3 = -8 NK(−2)=(−2)2×(−2)2×(−2)2=(−2)3=−8。 -
N K ( 2 ) = 64 N_K(2) = 64 NK(2)=64
-
N K ( 2 3 ) = 4 N_K(\sqrt[3]{2}) = 4 NK(32)=4
-
N K ( − 2 ) = − 8 N_K(\sqrt{-2}) = -8 NK(−2)=−8
-
N K ( α + 5 ) N_K(\alpha + 5) NK(α+5)的结果是一个复数表达式: ( 2 3 + 5 + 2 i ) 6 (\sqrt[3]{2} + 5 + \sqrt{2}i)^6 (32+5+2i)6
-
N K ( 2 3 − 2 + 1 ) N_K(\sqrt[3]{2}\sqrt{-2}+1) NK(32−2+1)的结果也是一个复数表达式: ( 1 + 1.12246204830937 2 i ) 6 (1 + 1.12246204830937\sqrt{2}i)^6 (1+1.122462048309372i)6
4. 迹 T T T
首先,找出 α \alpha α 的共轭元素。这涉及解决 f ( x ) = 0 f(x) = 0 f(x)=0 的方程,但这个方程过于复杂,无法用简单的代数方法解决。
然而,由于 α \alpha α 是 f ( x ) f(x) f(x) 的一个根,我们知道至少有六个共轭元素(包括 α \alpha α 本身),它们可能是实数或复数。
迹 T ( a ) T(a) T(a) 是所有共轭元素的和。对于简单的元素如 2 2 2 或 2 3 \sqrt[3]{2} 32,这些值在共轭元素下的表达式是明确的。
对于 α \alpha α 和更复杂的表达式,这些值将取决于 α \alpha α 的具体共轭元素。
-
T ( 2 ) T(2) T(2)
由于 2 2 2 是一个常数,它在每个共轭元素下的值都是 2 2 2。
因此, T ( 2 ) T(2) T(2) 是 2 2 2 与共轭元素的数量(这里是 6)的乘积:
T ( 2 ) = 2 × 6 = 12 T(2) = 2 \times 6 = 12 T(2)=2×6=12 -
T ( 2 3 ) T(\sqrt[3]{2}) T(32)
同样, 2 3 \sqrt[3]{2} 32 是一个常数,所以 T ( 2 3 ) T(\sqrt[3]{2}) T(32) 是 2 3 \sqrt[3]{2} 32 与共轭元素的数量的乘积:
T ( 2 3 ) = 2 3 × 6 T(\sqrt[3]{2}) = \sqrt[3]{2} \times 6 T(32)=32×6 -
T ( − 2 ) T(\sqrt{-2}) T(−2)
由于 − 2 \sqrt{-2} −2 是一个常数,其迹是:
T ( − 2 ) = − 2 × 6 T(\sqrt{-2}) = \sqrt{-2} \times 6 T(−2)=−2×6
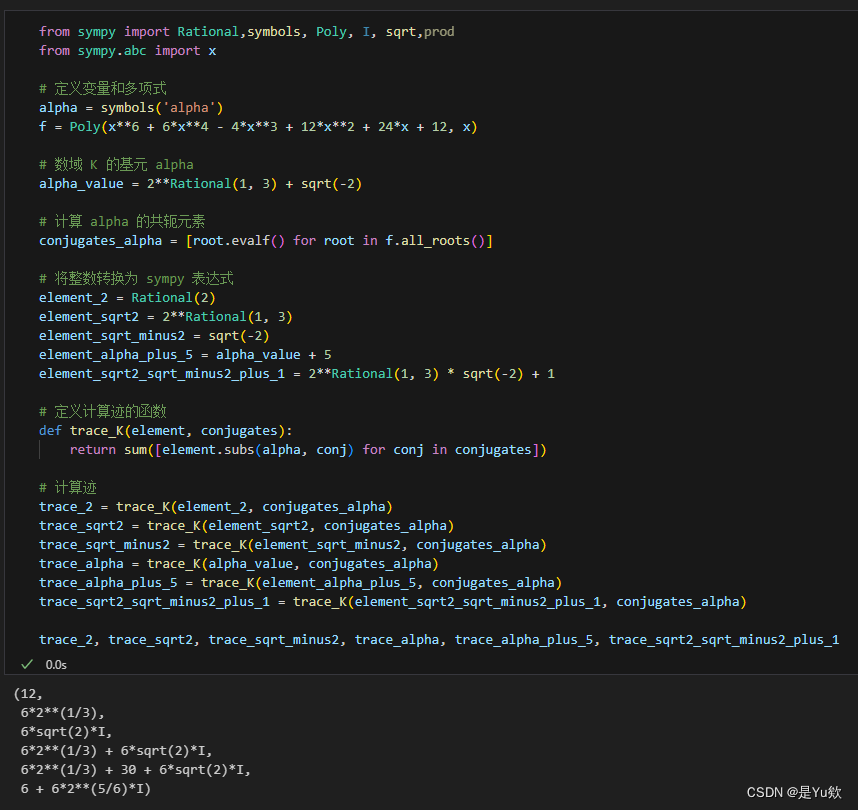
- T K ( 2 ) = 12 T_K(2) = 12 TK(2)=12
- T K ( 2 3 ) = 6 2 3 T_K(\sqrt[3]{2}) = 6\sqrt[3]{2} TK(32)=632
- T K ( − 2 ) T_K(\sqrt{-2}) TK(−2)的结果是一个纯虚数: 6 2 i 6\sqrt{2}i 62i
- T K ( α ) T_K(\alpha) TK(α)的结果是一个复数: 6 2 3 + 6 2 i 6\sqrt[3]{2} + 6\sqrt{2}i 632+62i
- T K ( α + 5 ) T_K(\alpha + 5) TK(α+5) 的结果也是一个复数: 6 2 3 + 30 + 6 2 i 6\sqrt[3]{2} + 30 + 6\sqrt{2}i 632+30+62i
- T K ( 2 3 − 2 + 1 ) T_K(\sqrt[3]{2}\sqrt{-2}+1) TK(32−2+1) 的结果也是一个复数: 6 + 6 ⋅ 2 5 / 6 i 6 + 6 \cdot 2^{5/6}i 6+6⋅25/6i
5. 数域 K K K 的迹 T K T_K TK
对于第5题,既然 α = 2 3 + − 2 \alpha = \sqrt[3]{2} + \sqrt{-2} α=32+−2,那么数域 K = Q ( α ) K = \mathbb{Q}(\alpha) K=Q(α) 实际上是 α \alpha α 的极小多项式的分裂域。这意味着在这个特定情况下,计算元素的迹和计算它在数域 K K K 中的迹是相同的过程。
因此,第5题和第4题的答案相同。
- T K ( 2 ) = 12 T_K(2) = 12 TK(2)=12
- T K ( 2 3 ) = 6 2 3 T_K(\sqrt[3]{2}) = 6\sqrt[3]{2} TK(32)=632
- T K ( − 2 ) T_K(\sqrt{-2}) TK(−2)的结果是一个纯虚数: 6 2 i 6\sqrt{2}i 62i
- T K ( α ) T_K(\alpha) TK(α)的结果是一个复数: 6 2 3 + 6 2 i 6\sqrt[3]{2} + 6\sqrt{2}i 632+62i
- T K ( α + 5 ) T_K(\alpha + 5) TK(α+5) 的结果也是一个复数: 6 2 3 + 30 + 6 2 i 6\sqrt[3]{2} + 30 + 6\sqrt{2}i 632+30+62i
- T K ( 2 3 − 2 + 1 ) T_K(\sqrt[3]{2}\sqrt{-2}+1) TK(32−2+1) 的结果也是一个复数: 6 + 6 ⋅ 2 5 / 6 i 6 + 6 \cdot 2^{5/6}i 6+6⋅25/6i