【原创】【改良莫队】

莫队算法：

常规的莫队算法，是将询问操作离线完成，根据左端点所在的块为第一优先，以右端点下标为第二优先进行排序，每两个相邻的询问都根据上一次询问的答案，通过重复“插入一个值/删除一个值”的操作，来得到下一个询问的答案。
但是，常规的莫队算法弊端有很多，比如需要同时支持快速插入/删除一个值，本文主要介绍一种莫队算法的修改版，以解决一些只能支持插入，不能支持直接删除，但支持撤回操作的问题（关于撤回操作的定义见下文）。

改良莫队：

其实算法的思想很简单，大体上和普通的莫队并无太大区别。
排序方式是一样的。
但是对于左端点所在的块，将询问分为不同的类分别处理。也就是说，我们一次只处理左端点在同一个块中的所有询问。

对于一类询问，有以下特点：其右端点呈不下降序列，左端点则位于同一个大小为 $\sqrt N$ 的块内
那么我们可以将这些询问分为两部分：

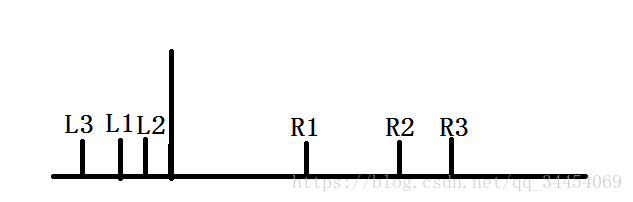
这里写代码片
对于右半部分，我们递增地插入元素，对于左半部分，每次询问后不保留，都是从拆分点向左依次加入。我们可以先向右扩大右端点，再向左扩大左端点，这样一来，所有不保留的操作都是依次进行的，之后再依次撤回即可。当前类处理完后，全部信息清空。最后的复杂度仍然是 $O(N\sqrt N)$ ，证明很直观也很简单，读者有兴趣可以自己思考。
读到这里，你可能对这种算法的实用性感到质疑：撤回操作和删除操作有什么区别吗？其实区别很大！
直接来看一个例题

例题

题号：CQBZOJ3611: 作业斯的监视
给出N个点，M条边的无向图，每条边有一个编号id
有Q次询问，每次询问给出两个值l,r，求仅保留编号id∈[l,r]的边时，图中的联通块个数，以及每个联通块大小的异或和。

样例输入：
4 6 3
1 2
2 3
3 4
1 3
2 4
1 4
1 3
2 5
3 4

样例输出：
1 4
1 4
2 2

用线段树分治等一系列算法都可以解决第一问，然而用本算法，就可以在 $O(N\sqrt NlogN)$ 的复杂度内以较短的代码求解。

其实大体解法就是上面的算法介绍的内容，只不过需要套进一个按秩合并的并查集中，撤回操作就是将之前连的边直接拆除。
这里就可以具体说明删除操作和撤回操作的不同之处了：
对于普通的莫队，并查集是无法支持的，因为每次删除时，其另一端点可能插入一些新的边，使得当前边删除后，仍然不会对连通性造成影响。
但对于这个算法，并查集就能够操作，因为这里的撤回操作，另一端点是不变的，因此当前边的连通性是能够确定的。

由于并查集是很经典的、使删除与撤回操作有明显区别的算法，并且实现较为简单，思路也不复杂，所以我选择并查集作为例题的数据结构。但并不意味着删除与撤回操作有区别的仅有这一个算法，所以这个改良是有一定实用价值的（自吹一下）。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
#define SF scanf
#define PF printf
#define MAXN 100010
using namespace std;
pair<int,int> edge[MAXN];
struct node{
    int l,r,id,b;
    pair<int,int> ans;
}que[MAXN];
int dep[MAXN],fa[MAXN],siz[MAXN],sum,tot;
bool cmp(const node &a,const node &b){
    if(a.b!=b.b)
        return a.b<b.b;
    return a.r<b.r;
}
struct opr{
    int px,py;
    int sizy,depy;
    opr () {}
    opr (int px1,int py1,int sizy1,int depy1):px(px1),py(py1),sizy(sizy1),depy(depy1) {}
};
stack<opr> del;
pair<int,int> ans[MAXN];
int get_fa(int x){
    int x1=x;
    while(fa[x]!=0)
        x=fa[x];
    return x;
}
void addedge(int x,int flag){
    int u=edge[x].first,v=edge[x].second;
    int fu=get_fa(u);
    int fv=get_fa(v);
    if(dep[fu]>dep[fv])
        swap(fu,fv);
    if(fu==fv)
        return ;
    if(flag==1)
        del.push(opr(fu,fv,siz[fv],dep[fv]));
    if(dep[fv]==dep[fu])
        dep[fv]++;
    fa[fu]=fv;
    sum=sum^siz[fu]^siz[fv];
    siz[fv]+=siz[fu];
    sum^=siz[fv];
    tot--;
}
void dework(){
    while(!del.empty()){
        opr now=del.top();
        int x=now.px,y=now.py,siz1=now.sizy,dep1=now.depy;
        fa[x]=0;
        sum=sum^siz[y]^siz1^(siz[y]-siz1);
        tot++;
        siz[y]=siz1;
        dep[y]=dep1;
        del.pop();
    }
}
int n,m,q,u,v;
int main(){
    SF("%d%d%d",&n,&m,&q);
    for(int i=1;i<=m;i++){
        SF("%d%d",&u,&v);
        edge[i]=make_pair(u,v);
    }
    for(int i=1;i<=q;i++){
        SF("%d%d",&u,&v);
        que[i].l=u;
        que[i].r=v;
        que[i].id=i;
    }
    int n1=sqrt(m);
    for(int i=1;i<=q;i++)
        que[i].b=que[i].l/n1+1;
    sort(que+1,que+q+1,cmp);
    sum=n%2,tot=n;
    int las=1;
    for(int i=1;i<=q;i++){
        if(que[i].b!=que[i-1].b){
            memset(fa,0,sizeof fa);
            for(int j=1;j<=n;j++)
                siz[j]=1;
            sum=n%2;
            tot=n;
            las=que[i].b*n1;
        }
        for(;las<=que[i].r;las++)
            addedge(las,0);
        for(int j=que[i].l;j<=min(que[i].r,que[i].b*n1-1);j++)
            addedge(j,1);
        que[i].ans=make_pair(tot,sum);
        dework();
    }
    for(int i=1;i<=q;i++)
        ans[que[i].id]=que[i].ans;
    for(int i=1;i<=q;i++)
        PF("%d %d\n",ans[i].first,ans[i].second);
}