学习博客:
http://www.cnblogs.com/Paul-Guderian/p/6933799.html
https://www.cnblogs.com/wsblm/p/10813007.html
【莫队算法】
·排序巧妙优化复杂度,带来NOIP前的最后一丝宁静。几个活蹦乱跳的指针的跳跃次数,决定着莫队算法的优劣……
·目前的题型概括为三种:普通莫队,树形莫队以及带修莫队。
若谈及入门,那么BZOJ2038的美妙袜子一题堪称顶尖。
【例题一】袜子
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=2038
·述大意:
进行区间询问[l,r],输出该区间内随机抽两次抽到相同颜色袜子的概率。
·分析:
首先考虑对于一个长度为n区间内的答案如何求解。题目要求Ans使用最简分数表示:那么分母就是n*n-n(表示两两袜子之间的随机组合),分子是一个累加和-n,累加的内容是该区间内每种颜色i出现次数sum[i]的平方。
将莫队算法抬上议程。莫队算法的思路是,离线情况下对所有的询问进行一个美妙的SORT(),然后两个指针l,r(本题是两个,其他的题可能会更多)不断以看似暴力的方式在区间内跳来跳去,最终输出答案。
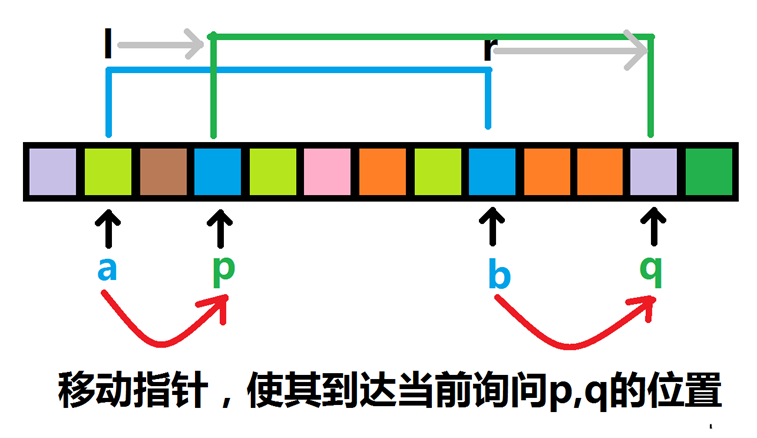
掌握一个思想基础:两个询问之间的状态跳转。如图,当前完成的询问的区间为[a,b],下一个询问的区间为[p,q],现在保存[a,b]区间内的每个颜色出现次数的sum[]数组已经准备好,[a,b]区间询问的答案Ans1已经准备好,怎样用这些条件求出[p,q]区间询问的Ans2?
考虑指针向左或向右移动一个单位,我们要付出多大的代价才能维护sum[]和Ans(即使得sum[],Ans保存的是当前[l,r]的正确信息)。我们美妙地对图中l,r的向右移动一格进行分析:
如图啦。l指针向右移动一个单位,所造成的后果就是:我们损失了一个绿色方块。那么怎样维护?美妙地,sum[绿色]减去1。那Ans如何维护?先看分母,分母从n2变成(n-1)2,分子中的其他颜色对应的部分是不会变的,绿色却从sum[绿色]2变成(sum[绿色]-1)2 ,为了方便计算我们可以直接向给Ans减去以前该颜色的答案贡献(即sum[绿色]2)再加上现在的答案贡献(即(sum[绿色]-1)2 )。同理,观赏下面的r指针移动,将是差不多的。
·如图r指针的移动带来的后果是,我们多了一个橙色方块。所以操作和上文相似,只不过是sum[橙色]++。
·回归正题地,我们美妙的发现,知道一个区间的信息,要求出旁边区间的信息(旁边区间指的是当前区间的一个指针通过加一减一得到的区间),竟只需要O(1)的时间。
·就算是这样,到这里为止的话莫队算法依旧无法焕发其光彩,原因是:如果我们以读入的顺序来枚举每个询问,每个询问到下一个询问时都用上述方法维护信息,那么在你脑海中会浮现出l,r跳来跳去的疯狂景象,疯狂之处在于最坏情况下时间复杂度为:O(n2)————如果要这样玩,那不如写一个暴力程序。
·“莫队算法巧妙地将询问离线排序,使得其复杂度无比美妙……”在一般做题时我们时常遇到使用排序来优化枚举时间消耗的例子。莫队的优化基于分块思想:对于两个询问,若在其l在同块,那么将其r作为排序关键字,若l不在同块,就将l作为关键字排序(这就是双关键字)。大米饼使用Be[i]数组表示i所属的块是谁。排序如:
·值得强调的是,我们是在对询问进行操作。
·时间复杂度分析(分类讨论思想):
首先,枚举m个答案,就一个m了。设分块大小为unit。
分类讨论:
①l的移动:若下一个询问与当前询问的l所在的块不同,那么只需要经过最多2*unit步可以使得l成功到达目标.复杂度为:O(m*unit)
②r的移动:r只有在Be[l]相同时才会有序(其余时候还是疯狂地乱跳,你知道,一提到乱跳,那么每一次最坏就要跳n次!),Be[l]什么时候相同?在同一块里面l就Be[]相同。对于每一个块,排序执行了第二关键字:r。所以这里面的r是单调递增的,所以枚举完一个块,r最多移动n次。总共有n/unit个块:复杂度为:O(n*n/unit)
总结:O(n*unit+n*n/unit)(n,m同级,就统一使用n)
根据基本不等式得:当unit为sqrt(n)时,得到莫队算法的真正复杂度:
O(n*sqrt(n))
·代码上来了(莫队喜欢while):
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; typedef long long LL; const int maxn=50000+50; LL a[maxn],b[maxn];//a 存输入的状态 b存当前区间每种袜子的个数 LL ans=0,block; struct query { LL l,r,num; }q[maxn]; struct ans1 { LL l,r; }A[maxn]; bool cmp(const query a,const query b) { // if(a.l==b.l) return a.r<b.r; if(a.l/block==b.l/block) return a.r<b.r; return a.l<b.l; } void solve(LL x,LL add) { ans-=b[a[x]]*(b[a[x]]-1); b[a[x]]+=add; ans+=b[a[x]]*(b[a[x]]-1); } LL gcd(LL a,LL b) { return a%b==0?b:(gcd(b,a%b)); } int main() { LL N,M; scanf("%lld%lld",&N,&M); block=sqrt(N); for(int i=1;i<=N;i++) { scanf("%lld",&a[i]); } for(int i=0;i<M;i++) { scanf("%lld%lld",&q[i].l,&q[i].r); q[i].num=i; } sort(q,q+M,cmp); LL L=1,R=0; for(int i=0;i<M;i++) { // cout<<"*"<<endl; LL ret=q[i].r-q[i].l+1; while(R<q[i].r)//往右走,袜子增加 { solve(R+1,1); R++; } while(R>q[i].r) { solve(R,-1);//往左走 袜子减少 R--; } while(L<q[i].l) { solve(L,-1);//往右走 袜子减少 L++; } while(L>q[i].l)//往左走 袜子增加 { solve(L-1,1); L--; } if(ans==0) A[q[i].num].l=0,A[q[i].num].r=1; else { LL g=gcd(ans,ret*(ret-1)); A[q[i].num].l=ans/g; A[q[i].num].r=ret*(ret-1)/g; } } // cout<<"**"<<endl; for(int i=0;i<M;i++) { printf("%lld/%lld\n",A[i].l,A[i].r); } return 0; }
·排序巧妙优化复杂度,带来NOIP前的最后一丝宁静。几个活蹦乱跳的指针的跳跃次数,决定着莫队算法的优劣……
·目前的题型概括为三种:普通莫队,树形莫队以及带修莫队。
若谈及入门,那么BZOJ2038的美妙袜子一题堪称顶尖。
【例题一】袜子
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=2038
·述大意:
进行区间询问[l,r],输出该区间内随机抽两次抽到相同颜色袜子的概率。
·分析:
首先考虑对于一个长度为n区间内的答案如何求解。题目要求Ans使用最简分数表示:那么分母就是n*n-n(表示两两袜子之间的随机组合),分子是一个累加和-n,累加的内容是该区间内每种颜色i出现次数sum[i]的平方。
将莫队算法抬上议程。莫队算法的思路是,离线情况下对所有的询问进行一个美妙的SORT(),然后两个指针l,r(本题是两个,其他的题可能会更多)不断以看似暴力的方式在区间内跳来跳去,最终输出答案。
掌握一个思想基础:两个询问之间的状态跳转。如图,当前完成的询问的区间为[a,b],下一个询问的区间为[p,q],现在保存[a,b]区间内的每个颜色出现次数的sum[]数组已经准备好,[a,b]区间询问的答案Ans1已经准备好,怎样用这些条件求出[p,q]区间询问的Ans2?
考虑指针向左或向右移动一个单位,我们要付出多大的代价才能维护sum[]和Ans(即使得sum[],Ans保存的是当前[l,r]的正确信息)。我们美妙地对图中l,r的向右移动一格进行分析:
如图啦。l指针向右移动一个单位,所造成的后果就是:我们损失了一个绿色方块。那么怎样维护?美妙地,sum[绿色]减去1。那Ans如何维护?先看分母,分母从n2变成(n-1)2,分子中的其他颜色对应的部分是不会变的,绿色却从sum[绿色]2变成(sum[绿色]-1)2 ,为了方便计算我们可以直接向给Ans减去以前该颜色的答案贡献(即sum[绿色]2)再加上现在的答案贡献(即(sum[绿色]-1)2 )。同理,观赏下面的r指针移动,将是差不多的。
·如图r指针的移动带来的后果是,我们多了一个橙色方块。所以操作和上文相似,只不过是sum[橙色]++。
·回归正题地,我们美妙的发现,知道一个区间的信息,要求出旁边区间的信息(旁边区间指的是当前区间的一个指针通过加一减一得到的区间),竟只需要O(1)的时间。
·就算是这样,到这里为止的话莫队算法依旧无法焕发其光彩,原因是:如果我们以读入的顺序来枚举每个询问,每个询问到下一个询问时都用上述方法维护信息,那么在你脑海中会浮现出l,r跳来跳去的疯狂景象,疯狂之处在于最坏情况下时间复杂度为:O(n2)————如果要这样玩,那不如写一个暴力程序。
·“莫队算法巧妙地将询问离线排序,使得其复杂度无比美妙……”在一般做题时我们时常遇到使用排序来优化枚举时间消耗的例子。莫队的优化基于分块思想:对于两个询问,若在其l在同块,那么将其r作为排序关键字,若l不在同块,就将l作为关键字排序(这就是双关键字)。大米饼使用Be[i]数组表示i所属的块是谁。排序如:
·值得强调的是,我们是在对询问进行操作。
·时间复杂度分析(分类讨论思想):
首先,枚举m个答案,就一个m了。设分块大小为unit。
分类讨论:
①l的移动:若下一个询问与当前询问的l所在的块不同,那么只需要经过最多2*unit步可以使得l成功到达目标.复杂度为:O(m*unit)
②r的移动:r只有在Be[l]相同时才会有序(其余时候还是疯狂地乱跳,你知道,一提到乱跳,那么每一次最坏就要跳n次!),Be[l]什么时候相同?在同一块里面l就Be[]相同。对于每一个块,排序执行了第二关键字:r。所以这里面的r是单调递增的,所以枚举完一个块,r最多移动n次。总共有n/unit个块:复杂度为:O(n*n/unit)
总结:O(n*unit+n*n/unit)(n,m同级,就统一使用n)
根据基本不等式得:当unit为sqrt(n)时,得到莫队算法的真正复杂度:
O(n*sqrt(n))
·代码上来了(莫队喜欢while):
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; typedef long long LL; const int maxn=50000+50; LL a[maxn],b[maxn];//a 存输入的状态 b存当前区间每种袜子的个数 LL ans=0,block; struct query { LL l,r,num; }q[maxn]; struct ans1 { LL l,r; }A[maxn]; bool cmp(const query a,const query b) { // if(a.l==b.l) return a.r<b.r; if(a.l/block==b.l/block) return a.r<b.r; return a.l<b.l; } void solve(LL x,LL add) { ans-=b[a[x]]*(b[a[x]]-1); b[a[x]]+=add; ans+=b[a[x]]*(b[a[x]]-1); } LL gcd(LL a,LL b) { return a%b==0?b:(gcd(b,a%b)); } int main() { LL N,M; scanf("%lld%lld",&N,&M); block=sqrt(N); for(int i=1;i<=N;i++) { scanf("%lld",&a[i]); } for(int i=0;i<M;i++) { scanf("%lld%lld",&q[i].l,&q[i].r); q[i].num=i; } sort(q,q+M,cmp); LL L=1,R=0; for(int i=0;i<M;i++) { // cout<<"*"<<endl; LL ret=q[i].r-q[i].l+1; while(R<q[i].r)//往右走,袜子增加 { solve(R+1,1); R++; } while(R>q[i].r) { solve(R,-1);//往左走 袜子减少 R--; } while(L<q[i].l) { solve(L,-1);//往右走 袜子减少 L++; } while(L>q[i].l)//往左走 袜子增加 { solve(L-1,1); L--; } if(ans==0) A[q[i].num].l=0,A[q[i].num].r=1; else { LL g=gcd(ans,ret*(ret-1)); A[q[i].num].l=ans/g; A[q[i].num].r=ret*(ret-1)/g; } } // cout<<"**"<<endl; for(int i=0;i<M;i++) { printf("%lld/%lld\n",A[i].l,A[i].r); } return 0; }