【博弈论】【第四章】不完全信息静态博弈（二）

（书接上文）

五、贝叶斯博弈与混合战略均衡:

纯化定理( purification theorem;Harsanyi，1973):完全信息静态博弈中的一个混合战略博弈几乎总是可以被解释成一个有少量不完全信息的近似博弈的一个纯战略贝叶斯纳什均衡。
进一步可理解成“一个混合战略纳什均衡的根本特征不是参与人以随机的方法选择战略（即行为)，而是各参与人对其他参与人的选择不能确定，这种不确定性既可以是随机性引起，也可以是少量信息的不完全性引起。”
（大白话翻译就是：一个混合战略的纳什均衡可以简单的分成几个纯战略纳什均衡问题）

【例题】夫妻之争

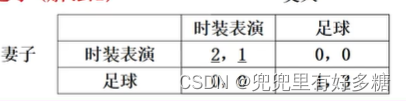
有两个纯战略纳什均衡（时装，时装)、(足球，足球)，还有一个混合战略纳什均衡，即妻子以3/4的概率选时装，以1/ 4的概率选足球，丈夫以1/3的概率选时装，以2 / 3的概率选足球。
以上是前两章解决问题的方法。
还可以用一中概率的方法解决该问题：

【解法一】
丈夫对妻子看时装表演的得益不完全清楚，妻子对丈夫看足球的得益也不完全清楚。此时我们就把一个完全信息的静态博弈转换成了一个不完全信息的静态博弈。
这个不完全信息表现在丈夫对妻子看时装表演的得益不完全清楚，妻子对丈夫看足球的得益也不完全清楚。但我们要对其概率分布有一个了解，此处假设这个分布是一个$[0,x]$的均匀分布，那么密度函数就是$1/x$。我们用参与人1表示妻子，参与人2表示丈夫。
用下面这式子来计算妻子如何达到最佳收益（就是给定丈夫的选择的情况下妻子如何选择，从而能使得妻子自己的期望效用最大化）
$$\begin{array}{rl}& \underset{t_1\in T_1}{\max }{\int }_0^x\left(s_1,s_2^{\ast }\right)\frac{1}{x}d{t}_2\\ & =\underset{t_1\in T_1}{\max }\{\begin{array}{l}\left[{\int }_0^{t_2^{\ast }}\left(s_1=a_1,s_2^{\ast }=a_1\right)\frac{1}{x}d{t}_2+{\int }_{t_2^{\ast }}^x\left(s_1=a_1,s_2^{\ast }=a_2\right)\frac{1}{x}d{t}_2\right]if{t}_1\ge t_1^{\ast }\\ （当妻子的想看服装秀的程度很高的时候，不论丈夫选择什么，妻子都会选择服装秀）\\ \left[{\int }_0^{t_2^{\ast }}\left(s_1=a_2,s_2^{\ast }=a_1\right)\frac{1}{x}d{t}_2+{\int }_{t_2^{\ast }}^x\left(s_2=a_2,s_2^{\ast }=a_2\right)\frac{1}{x}d{t}_2\right]if{t}_1<t_1^{\ast }\\ （当妻子的没有那么想看服装秀的时候，不论丈夫选择什么，妻子都会选择足球）\end{array}\\ & =\underset{t_1\in T_1}{\max }\{\begin{array}{l}\left[{\int }_0^{t_2^{\ast }}\left(2+t_1\right)\frac{1}{x}d{t}_2+{\int }_{t_2^{\ast }}^{x}0\times \frac{1}{x}d{t}_2\right]=\frac{\left(2+t_1\right)t_2^{\ast }}{x}\\ \left[{\int }_0^{t_2^{\ast }}0\times \frac{1}{x}d{t}_2+{\int }_{t_2^{\ast }}^{x}1\times \frac{1}{x}d{t}_2\right]=\frac{x-t_2^{\ast }}{x}\\ \Rightarrow \frac{\left(2+t_1^{\ast }\right)t_2^{\ast }}{x}=\frac{x-t_2^{\ast }}{x}if{t}_1=t_1^{\ast }\\ (让妻子选择时装秀或者选择足球的期望收益相等，这时就是妻子最佳的得益所对应的参数分布)\end{array}\end{array}$$
$$\begin{array}{rl}& \underset{t_2\in T_2}{\max }{\int }_0^x\left(s_1^{\ast },s_2\right)\frac{1}{x}d{t}_1\\ & =\underset{t_2\in T_2}{\max }\{\begin{array}{l}\left[{\int }_0^{t_1^{\ast }}\left(s_1^{\ast }=a_2,s_2=a_1\right)\frac{1}{x}d{t}_1+{\int }_{t_1^{\ast }}^x\left(s_1^{\ast }=a_1,s_2=a_1\right)\frac{1}{x}d{t}_1\right]if{t}_2<t_2^{\ast }\\ \left[{\int }_0^{t_1^{\ast }}\left(s_1^{\ast }=a_2,s_2=a_2\right)\frac{1}{x}d{t}_1+{\int }_{t_1^{\ast }}^x\left(s_1^{\ast }=a_1,s_2=a_2\right)\frac{1}{x}d{t}_1\right]if{t}_2\ge t_2^{\ast }\end{array}\\ & =\underset{t_2\in T_2}{\max }\{\begin{array}{l}\left[{\int }_0^{t_1^{\ast }}0\times \frac{1}{x}d{t}_1+{\int }_{t_1^{\ast }}^{x}1\times \frac{1}{x}d{t}_1\right]=\frac{x-t_1^{\ast }}{x}\\ \left[{\int }_0^{t_1^{\ast }}\left(3+t_2\right)\times \frac{1}{x}d{t}_1+{\int }_{t_2^{\ast }}^{x}0\times \frac{1}{x}d{t}_1\right]=\frac{\left(3+t_2\right)t_1^{\ast }}{x}\\ \Rightarrow \frac{x-t_1^{\ast }}{x}=\frac{\left(3+t_2^{\ast }\right)t_1^{\ast }}{x}if{t}_2=t_2^{\ast }\end{array}\end{array}$$

( 2 + t 1 ∗ ) t 2 ∗ x = x − t 2 ∗ x x − t 1 ∗ x = ( 3 + t 2 ∗ ) t 1 ∗ x } ⇒ { t 1 ∗ = − 3 + 9 + 3 x 2 t 2 ∗ = − 6 + 2 9 + 3 x 3 a ∗ = { s 1 ∗ ( T 11 ) = a 1 , s 1 ∗ ( T 12 ) = a 2 ; s 2 ∗ ( T 21 ) = a 1 , s 2 ∗ ( T 22 ) = a 2 } T 11 = [ t 1 ∗ , x ] , T 12 = [ 0 , t 1 ∗ ] T 21 = [ 0 , t 2 ∗ ] , T 22 = [ t 2 ∗ , x ] \begin{aligned} &\left.\begin{array}{l} \frac{\left(2+t_1^*\right) t_2^*}{x}=\frac{x-t_2^*}{x} \\ \frac{x-t_1^*}{x}=\frac{\left(3+t_2^*\right) t_1^*}{x} \end{array}\right\} \Rightarrow\left\{\begin{array}{l} t_1^*=\frac{-3+\sqrt{9+3 x}}{2} \\ t_2^*=\frac{-6+2 \sqrt{9+3 x}}{3} \end{array}\right.\\ &\begin{aligned} & a^*=\left\{s_1^*\left(T_{11}\right)=a_1, s_1^*\left(T_{12}\right)=a_2 ; s_2^*\left(T_{21}\right)=a_1, s_2^*\left(T_{22}\right)=a_2\right\} \\ & T_{11}=\left[t_1^*, x\right], T_{12}=\left[0, t_1^*\right] T_{21}=\left[0, t_2^*\right], T_{22}=\left[t_2^*, x\right] \end{aligned} \end{aligned} ​x(2+t1∗​)t2∗​​=xx−t2∗​​xx−t1∗​​=x(3+t2∗​)t1∗​​​}⇒{ t1∗​=2−3+9+3x ​​t2∗​=3−6+29+3x ​​​​a∗={ s1∗​(T11​)=a1​,s1∗​(T12​)=a2​;s2∗​(T21​)=a1​,s2∗​(T22​)=a2​}T11​=[t1∗​,x],T12​=[0,t1∗​]T21​=[0,t2∗​],T22​=[t2∗​,x]​​
我们从上面这个结论也可以证明混合概率模型的求解结果：
$$\begin{array}{rl}& P\left(0\le t_1^{\ast }<\frac{-3+\sqrt{9+3x}}{2}\right)=\frac{-3+\sqrt{9+3x}}{2x}\\ & =\frac{3}{2(3+\sqrt{9+3x})}{|}_{x\to 0}=\frac{1}{4}\\ & P\left(0\le t_2^{\ast }<\frac{-6+2\sqrt{9+3x}}{3}\right)=\frac{-6+2\sqrt{9+3x}}{3x}\\ & =\frac{4}{6+2\sqrt{9+3x}}{|}_{x\to 0}=\frac{1}{3}\end{array}$$
【解法二】
设妻子的战略:当$t_w>W$时，选择时装表演，否则选择足球赛;丈夫的战略与妻子相似:当$t_h>h$时，选择足球赛，否则选时装表演。在上述双方的战略下，因为都是$[0,x]$上的标准分布，所以妻子选时装的概率为$(x-w)/x$，选足球赛的概率为$w/x$;丈夫选时装表演的概率为$h/x$，选足球赛的概率为$(x—h）/x$。为了使双方上述战略组合成为贝叶斯纳什均衡，参数$W$和$h$必须取恰当的数值。
从妻子的角度，假设已知丈夫已经采用了上述战略，则她选时装表演和足球赛的期望得益分别为:
$$\begin{array}{c}\frac{h}{x}\left(2+t_w\right)+\frac{x-h}{x}\times 0=\frac{h}{x}\left(2+t_w\right)\frac{h}{x}\times 0+\frac{x-h}{x}\times 1=\frac{x-h}{x}\\ w=\frac{x}{h}-3\end{array}$$
同样的，假设妻子已采用了前述临界值战略，则丈夫选择足球赛和时装表演的期望得益分别为:
$$\begin{array}{rl}& \frac{w}{x}\left(3+t_h\right)+\frac{x-w}{x}\times 0=\frac{w}{x}\left(3+t_h\right)\\ & \frac{w}{x}\times 0+\frac{x-w}{x}\times 1=\frac{x-w}{x}\end{array}$$
当选足球的期望得益不小于选时装表演的期望得益时，丈夫选择足球赛，即：
$t_h>=\frac{x}{w}-4$，由此可得：$h=\frac{x}{w}-4$.
$$\{\begin{array}{l}w=\frac{x}{h}-3\\ h=\frac{x}{w}-4\end{array}$$
$$\{\begin{array}{l}w=\frac{-3\pm \sqrt{9+3x}}{2}=\frac{-3+\sqrt{9+3x}}{2}\\ h=\frac{-6\pm 2\sqrt{9+3x}}{3}=\frac{-6+2\sqrt{9+3x}}{3}\end{array}$$
当参数W和h由上述两式决定时，容易证明双方的前述林觉战略构成贝叶斯纳什均衡。根据上述W和h的值，妻子选择时装表演的概率是：
$$\frac{x-w}{x}=1-\frac{w}{x}=1-\frac{-3+\sqrt{9+3x}}{2x}$$
丈夫选择足球赛的概率是：
$$\frac{x-h}{x}=1-\frac{h}{x}=1-\frac{-6+2\sqrt{9+3x}}{3x}$$
当x趋近于0时，即不完全信息接近消失或微不足道时，上述两概率分别趋向于3/4和2/3，而这也正是完全信息夫妻之争博弈的混合战略均衡的随机选择的概率。因此混合战略均衡可以看作是有极少量不完全信息的静态贝叶斯博弈的贝叶斯纳什均衡，这样就证明了海萨尼的结论是成立的。

【例题】非线性定价
假定有一个垄断厂商，以不变的边际成本$c$生产某种产品。当厂商出售$q\ge 0$数量的商品给消费者时，从消费者处获取数量$T$的货币;而消费者消费$q$数量的商品并支付$T$的费用时获得的效用为$u(q,T,\theta )=\theta v(q)-T$。这里$\theta V(q)$是消费者总剩余，$V(.)$是一个确定的关于$q$的函数，它满足$V(0)=0,V^{\prime }>0，V^{\prime \prime }<0$;$\theta$是消费者的类型信息，它的取值可能是${\theta }_1$或${\theta }_2$,${\theta }_2>{\theta }_1>0$。假定总人口中${\theta }_1$类型消费者的比例为$p_1$，${\theta }_2$类型消费者的比例为$p_2$，且 $p_1+p_2=1$。证明:企业的利润最大化行为（战略最优）意味着如下条件成立:
(1) ${\theta }_2{V}^{\prime }\left(q_2\right)=c$;
(2) ${\theta }_1{V}^{\prime }\left(q_1\right)=\frac{c}{1-\frac{p_2\left({\theta }_2-{\theta }_1\right)}{p_1{\theta }_1}}$

【解】
首先理解题意：$V(q)$是一个关于购买商品数量$q$的函数，其一阶微分大于零，二阶微分小于零，意思是随着消费者购买的商品数量逐渐递增，他认为该商品能给他带来的边际效用逐渐递减，这是一个变化率类似于对数函数的函数。
其次，$V(q)$是一个商品本身有的效用属性，但是由于消费者的类型不一样，所以给消费者带来的效用也不一样，比如辣椒本身有其固有的价值，但是对于喜欢吃辣的人带来的效用就会比给不喜欢吃辣的人带来的效用更高，这就是由消费者类型影响的。
下面让我们证明：两个参与人类型对应的商品效用：对于${\theta }_1$，当其消费数量为$q_2$时，其边际效用等于边际成本。对于${\theta }_2$，当其消费数量为$q_1$时，其边际效用大于边际成本，对于特别想要这个商品的，效用等于边际成本，对于不太想要这个商品的，其边际效用大于边际成本。
证明：
该博弈过程为厂商开出一个价$T(q)$，消费者要么接受要么拒绝。因此，公司将有两套方案:
$(q_1,T_1)$卖给${\theta }_1$类型的消费者，$(q_2,T_2)$卖给${\theta }_2$类型的消费者。
公司的期望收益为:$E{u}_0=p_1(T_1-c{q}_1)+p_2(T_2-c{q}_2)$
上面这些都是卖方开出的条件，至于买方是否会接受这样的条件，还有一个参与约束，就是买方衡量这个条件是否符合自己的利益：
参与约束(IR, individual - rationality):
$$\begin{gathered} (I{R}_1){\theta }_{1}V(q_1)-T_1\ge 0 \\ (I{R}_2){\theta }_{2}V(q_2)-T_2\ge 0 \end{gathered}$$
还有一个问题就是，公司是针对不同人群制定的不同方案，对于${\theta }_1$这类人群，制定的是$(q_1,T_1)$，针对${\theta }_2$这类人群，制定的是
$(q_2,T_2)$。所以需要保证${\theta }_1$在$(q_1,T_1)$准则下消费会得到最大的利益，而不是最后他们发现在$(q_2,T_2)$准则下消费会得到更好的利益，如果这样的话就说明公司消费计划制定错误，所以就有以下激励相容：
激励相容(C, incentive - compatibility)约束:
$$\begin{gathered} (I{C}_1){\theta }_{1}V(q_1)-T_1\ge {\theta }_{1}V(q_2)-T_2 \\ (I{C}_2){\theta }_{2}V(q_2)-T_2\ge {\theta }_{2}V(q_1)-T_1 \end{gathered}$$
所以博弈论在求解的时候其实也是一个多约束条件下的优化问题，所以他也有相应的优化算法来求解这种问题。
若$I{R}_1$和$I{C}_2$满足，由$(I{R}_1){\theta }_{1}V(q_1)-T_1\ge 0\to {\theta }_{1}V(q_1)\ge T_1$
$$\begin{array}{rl}{\theta }_{2}V\left(q_2\right)-T_2\ge {\theta }_{2}V\left(q_1\right)-T_1& \Rightarrow {\theta }_{2}V\left(q_2\right)-T_2\ge {\theta }_{2}V\left(q_1\right)-{\theta }_{1}V\left(q_1\right)\\ & =\left({\theta }_2-{\theta }_1\right)V\left(q_1\right)\ge 0\\ V\left(q_1\ne 0\right)>0,{\theta }_2-{\theta }_1>0\Rightarrow & {\theta }_{2}V\left(q_2\right)-T_2>0\end{array}$$
因此，厂商战略最优时，$I{R}_1$必成立于等号，否则对于任意小的$\epsilon$有：
$\left(I{C}_1\right){\theta }_{1}V\left(q_1\right)-\left(T_1+\epsilon \right)\ge {\theta }_{1}V\left(q_2\right)-\left(T_2+\epsilon \right)$
$$\left(I_2\right){\theta }_{2}V\left(q_2\right)-\left(T_2+\epsilon \right)\ge {\theta }_{2}V\left(q_1\right)-\left(T_1+\epsilon \right)$$
这不符合厂商最优化策略，所以${\theta }_{1}V(q_1)=T_1$
于是有：
$$\begin{array}{rl}& {\theta }_{2}V\left(q_2\right)-T_2={\theta }_{2}V\left(q_1\right)-T_1={\theta }_{2}V\left(q_1\right)-{\theta }_{1}V\left(q_1\right)\\ & \Rightarrow T_2={\theta }_{2}V\left(q_2\right)-{\theta }_{2}V\left(q_1\right)+{\theta }_{1}V\left(q_1\right)\\ & E{u}_0=p_1\left(T_1-c{q}_1\right)+p_2\left(T_2-c{q}_2\right)\\ & E{u}_0=p_1\left({\theta }_{1}V\left(q_1\right)-c{q}_1\right)+p_2\left[{\theta }_{2}V\left(q_2\right)-{\theta }_{2}V\left(q_1\right)+{\theta }_{1}V\left(q_1\right)-c{q}_2\right)]\\ & =\left[p_1{\theta }_1-p_2\left({\theta }_2-{\theta }_1\right)\right]V\left(q_1\right)-p_{1}c{q}_1+p_2\left[{\theta }_{2}V\left(q_2\right)-c{q}_2\right]\end{array}$$
分别求一节条件得：
${\theta }_2{V}^{\prime }(q_2)=c$
${\theta }_1{V}^{\prime }(q_1)=\frac{c}{1-\frac{p_2({\theta }_2-{\theta }_1)}{p_1{\theta }_1}}$