不完全信息静态博弈
一、海萨尼转换(把不完全信息静态博弈转换为完全信息静态博弈来求解)
引入虚拟的参与人-“自然”(nature);自然首先行动决定参与人的特征(成本函数),参与人知道自己的特征,其他参与人不知道。这样,上述不完全信息博弈就转换为完全但不完美信息博弈(game of complete but imperfect inf ormation)。
后行动者不知道先行动者具体采取哪种方案,这种叫做不完美
上面这个转换为完全信息静态博弈,但是后行动者仍然不知道自然对先行动者分配的资源是多少,先行动者也不知道后行动者的资源是多少。所以是不完美的模型的一种。就是双方都不知道对方的特征。
海萨尼转换主要就是把对支付收益的不了解转换为了对对方特征的不了解。对对方的类型不了解。
1“海萨尼转换”的基本思路
·将对得益的不了解转化为对类型的不了解。
- “自然”先为其他每个参与人抽取他们的类型,抽取的这些类型构成类型向量。
- “自然”让每个参与人知道自己的类型,但却不让其他参与人知道。
- 除“自然”以外的其他参与人同时从各自的行为空间中选择行动方案。
- 除“自然”以外,其余参与人各自取得得益。
2不完全信息静态博弈的表述
·在不完全信息静态博弈中,参与人的行动空间可能依赖于它的类型,行动空间是类型依存的( type - contingent)。
”行动空间是类型依存的( type - contingent)“这句话简单来说就是好人做好事,坏人做坏事。就是他会选择什么样的行动,与他本身是什么类型是密切相关的。
G = { A 1 , A 2 , ⋯ , A n ; t 1 , t 2 , ⋯ , t n ; p 1 , p 2 , ⋯ , p n ; u 1 , u 2 , ⋯ , u n } p i ( t − i / t i ) = p i ( t i / t − i ) p ( t − i ) p ( t i ) = p ( t − i , t i ) ∑ t − i ∈ T − i p ( t − i , t i ) v i = ∑ t − i p i ( t − i / t i ) u i ( a i ( t i ) , a − i ( t − i ) ; t i , t − i ) \begin{gathered} G=\left\{A_1, A_2, \cdots, A_n ; t_1, t_2, \cdots, t_n ; p_1, p_2, \cdots, p_n ; u_1, u_2, \cdots, u_n\right\} \\ p_i\left(t_{-i} / t_i\right)=\frac{p_i\left(t_i / t_{-i}\right) p\left(t_{-i}\right)}{p\left(t_i\right)}=\frac{p\left(t_{-i}, t_i\right)}{\sum_{t_{-i} \in T_{-i}} p\left(t_{-i}, t_i\right)} \\ v_i=\sum_{t_{-i}} p_i\left(t_{-i} / t_i\right) u_i\left(a_i\left(t_i\right), a_{-i}\left(t_{-i}\right) ; t_i, t_{-i}\right) \end{gathered} G={ A1,A2,⋯,An;t1,t2,⋯,tn;p1,p2,⋯,pn;u1,u2,⋯,un}pi(t−i/ti)=p(ti)pi(ti/t−i)p(t−i)=∑t−i∈T−ip(t−i,ti)p(t−i,ti)vi=t−i∑pi(t−i/ti)ui(ai(ti),a−i(t−i);ti,t−i)
- 其中A是每个参与人自己可选的方案组合,是一个向量,n表示第几个参与人;t便表示每个人的类型,每个人类型可能相同也可能不同;
- p是每个人的各个类型对应的概率分布;
- 针对于每种战略组合的收益值,用u来表示。
- 所以这个模型比原来的完全信息静态博弈就是增加了两部分,一部分是每个人的可能类型,一部分是每个人的类型的概率分布。而完全信息静态博弈中每个人的类型都是确定的,所以也不会存在相应的概率分布,或者说概率分布都是1。
- 参与人 i i i的类型是 t i t_i ti的时候,他推断其他参与人 − i -i −i的类型属于 t t t这种类型的概率就称为 p i ( t − i / t i ) p_i\left(t_{-i} /t_i\right) pi(t−i/ti)。然后用概率论方法把他展开就是后面的式子。
- u i ( a i ( t i ) , a − i ( t − i ) ; t i , t − i ) u_i\left(a_i\left(t_i\right), a_{-i}\left(t_{-i}\right) ; t_i, t_{-i}\right) ui(ai(ti),a−i(t−i);ti,t−i)表示的就是参与人 i i i根据自己的类型 t i t_i ti选择合适于自己的战略选择 a i a_i ai,其他参与人 − i -i −i根据他们自己的类型选择合适于他们的战略选择 a − i a_{-i} a−i。这个战略组合就对应一个收益,而这个收益是有概率的,概率为p。因为参与人选择这个战略组合是有概率的。所以把所有的战略组合的概率与其收益相乘求和我们就得到了收益的期望。
3.贝叶斯纳什均衡( Bayesian Nash equilibrium)
n人 G = { A 1 , A 2 , ⋯ , A n ; t 1 , t 2 , ⋯ , t n ; p 1 , p 2 , ⋯ , p n ; u 1 , u 2 , ⋯ , u n } G=\left\{A_1, A_2, \cdots, A_n ; t_1, t_2, \cdots, t_n ; p_1, p_2, \cdots, p_n ; u_1, u_2, \cdots, u_n\right\} G={
A1,A2,⋯,An;t1,t2,⋯,tn;p1,p2,⋯,pn;u1,u2,⋯,un} 纯战略贝叶斯纳什均衡是一个类型依存战略组合 { a i ∗ ( t i ) } i = 1 n \left\{a_i^*(t_i)\right\}_{i=1}^n {
ai∗(ti)}i=1n,其中每个参与人i在给定自己的类型和其他参与人类型依存战略 a − i ∗ ( t − i ) a_{-i}^*(t_{-i}) a−i∗(t−i)的情况下最大化自己的期望效用函数v;。换言之,战略组合 { a i ∗ ( t i ) } i = 1 n \left\{a_i^*(t_i)\right\}_{i=1}^n {
ai∗(ti)}i=1n是一个贝叶斯纳什均衡,如果对于所有的参与人 i i i:
a ∗ = ( a 1 ∗ ( t i ) , ⋯ , a n ∗ ( t n ) ) a i ∈ A i ( t i ) a i ∗ ( t i ) = arg max ∑ t − i p i ( t − i / t i ) u i ( a i ( t i ) , a − i ( t − i ) ; t i , t − i ) \begin{aligned} & a^*=\left(a_1^*\left(t_i\right), \cdots, a_n^*\left(t_n\right)\right) \quad a_i \in A_i\left(t_i\right) \\ & a_i^*\left(t_i\right)=\arg \max \sum_{t_{-i}} p_i\left(t_{-i} / t_i\right) u_i\left(a_i\left(t_i\right), a_{-i}\left(t_{-i}\right) ; t_i, t_{-i}\right) \end{aligned} a∗=(a1∗(ti),⋯,an∗(tn))ai∈Ai(ti)ai∗(ti)=argmaxt−i∑pi(t−i/ti)ui(ai(ti),a−i(t−i);ti,t−i)
二、例题
【例1】不完全信息古诺模型
两寡头厂商市场需求为 P ( Q ) = a − Q P(Q) =a-Q P(Q)=a−Q, Q = q 1 + q 2 Q=q_1+q_2 Q=q1+q2。厂商1的边际成本为 C C C且是共同知识,而厂商2成本是私人信息,厂商1只知道有高、低两种可能, C H C_H CH的概率为 θ \theta θ, C L C_L CL的概率为 1 − θ 1-\theta 1−θ, C H > C L C_H>C_L CH>CL。两厂商均无固定成本。
厂商2在高边际成本时会选择较低产量,而在低边际成本时选择较高产量。设厂商1的最佳产量为 q 1 ∗ q_1^* q1∗,厂商2边际成本为 C H C_H CH时的最佳产量为 q 2 ( C H ) q_2(C_H) q2(CH),边际成本为 C L C_L CL时的最佳产量为 q 2 ∗ ( C L ) q_2^*(C_L) q2∗(CL),则根据上面的假设,
q 2 ∗ ( C H ) 应满足: max q 2 [ ( a − q 1 ∗ − q 2 ) − C H ] q 2 q 2 ∗ ( C L ) 应满足: max q 2 [ ( a − q 1 ∗ − q 2 ) − C L ] q 2 q 1 ∗ 应满足: max q 1 { θ ( a − q 1 − q 2 ∗ ( C H ) − C 1 ] q 1 + ( 1 − θ ) [ a − q 1 − q 2 ∗ ( C L ) − C 1 ] q h } \begin{array}{ll} \boldsymbol{q}_2^*\left(\boldsymbol{C}_H\right) \text { 应满足: } & \max _{q_2}\left[\left(a-q_1^*-q_2\right)-C_H\right] q_2 \\ \boldsymbol{q}_2^*\left(\boldsymbol{C}_L\right) \text { 应满足: } & \max _{q_2}\left[\left(a-q_1^*-q_2\right)-C_L\right] q_2 \\ \boldsymbol{q}_1^* \text { 应满足: } & \max _{q_1}\left\{\theta\left(a-q_1-q_2^*\left(C_H\right)-C_1\right] q_1+(1-\theta)\left[a-q_1-q_2^*\left(C_L\right)-C_1\right] q_h\right\} \end{array} q2∗(CH) 应满足: q2∗(CL) 应满足: q1∗ 应满足: maxq2[(a−q1∗−q2)−CH]q2maxq2[(a−q1∗−q2)−CL]q2maxq1{
θ(a−q1−q2∗(CH)−C1]q1+(1−θ)[a−q1−q2∗(CL)−C1]qh}
上述三个最大值问题的一阶条件为:
q 2 ∗ ( C H ) = a − q 1 ∗ − C H 2 q 2 ∗ ( C L ) = a − q 1 ∗ − C L 2 q 1 ∗ = 1 2 { θ [ ( a − q 2 ∗ ( C H ) − C 1 ] + ( 1 − θ ) [ a − q 2 ∗ ( C L ) − C 1 ] } \begin{aligned} & q_2^*\left(C_H\right)=\frac{a-q_1^*-C_H}{2} \quad q_2^*\left(C_L\right)=\frac{a-q_1^*-C_L}{2} \\ & q_1^*=\frac{1}{2}\left\{\theta\left[\left(a-q_2^*\left(C_H\right)-C_1\right]+(1-\theta)\left[a-q_2^*\left(C_L\right)-C_1\right]\right\}\right. \end{aligned} q2∗(CH)=2a−q1∗−CHq2∗(CL)=2a−q1∗−CLq1∗=21{
θ[(a−q2∗(CH)−C1]+(1−θ)[a−q2∗(CL)−C1]}
解由这三个方程构成的方程组,得:
q 2 ∗ ( C H ) = a − 2 C H + C 1 3 + 1 − θ 6 ( C H − C L ) > a − 2 c 2 + c 1 3 q 2 ∗ ( C L ) = a − 2 C L + C 1 3 − θ 6 ( C H − C L ) < a − 2 c 2 + c 1 3 q 1 ∗ = a − 2 C 1 + θ C H + ( 1 − θ ) C L 3 \begin{aligned} & q_2^*\left(C_H\right)=\frac{a-2 C_H+C_1}{3}+\frac{1-\theta}{6}\left(C_H-C_L\right)>\frac{a-2 c_2+c_1}{3} \\ & q_2^*\left(C_L\right)=\frac{a-2 C_L+C_1}{3}-\frac{\theta}{6}\left(C_H-C_L\right)<\frac{a-2 c_2+c_1}{3} \\ & q_1^*=\frac{a-2 C_1+\theta C_H+(1-\theta) C_L}{3} \end{aligned} q2∗(CH)=3a−2CH+C1+61−θ(CH−CL)>3a−2c2+c1q2∗(CL)=3a−2CL+C1−6θ(CH−CL)<3a−2c2+c1q1∗=3a−2C1+θCH+(1−θ)CL
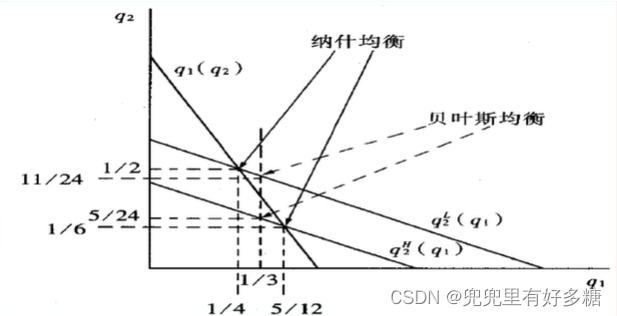
我们带入具体的数值( a = 2 , c 1 = 1 , c L = 3 / 4 , c H = 5 / 4 , θ = 1 / 2 a=2,c_1=1,c_L=3/4,c_H=5/4,\theta=1/2 a=2,c1=1,cL=3/4,cH=5/4,θ=1/2)计算一下可画出如上的图形。可以看到,低成本厂商的纳什均衡要比贝叶斯均衡的产量低,而高成本厂商的纳什均衡要比贝叶斯均衡的产量高。
【例2】一级密封价格拍卖(first-price-sealed bid auction)
设风险中性的两个投标人(bidder)为参与人1、2,他们对拍品的估价分别为 V 1 V_1 V1和 V 2 V_2 V2, V 1 V_1 V1, V 2 V_2 V2是 [ 0 , 1 ] [0,1] [0,1]上的标准分布,参与人 i i i用价格 P P P拍得拍品的得益为 V i − P V_i-P Vi−P。再设两参与人知道自己的估价和另一方估价的概率分布。参与人 i i i的行为就是其标价 b i b_i bi(不会超出 [ 0 , 1 ] [0,1] [0,1])。
【解】
参与人 i i i的得益函数:
u i = u i ( b 1 , b 2 , v 1 , v 2 ) = { v i − b i i f b i > b j ( v i − b i ) / 2 i f b i = b j 0 i f b i < b j u_i=u_i\left(b_1, b_2, v_1, v_2\right)= \begin{cases}v_i-b_i & i f b_i>b_j \\ \left(v_i-b_i\right) / 2 & i f b_i=b_j \\ 0 & i f b_i<b_j\end{cases} ui=ui(b1,b2,v1,v2)=⎩
⎨
⎧vi−bi(vi−bi)/20ifbi>bjifbi=bjifbi<bj
怎么理解上面这个得益函数呢?参与人i报的价要比参与人j的高,参与人i才能中标,这也就是第一种情况,中标之后,就是以你的报价来成交,所以你付出的成本就是报价 b i b_i bi,而我们内心的估价当然时比报价高的,我们觉得有自己的估值大于实际价格才会买他,所以我们的得益就是内心的估价减去实际付出的成本,也即 v i − b i v_i-b_i vi−bi
而当两人报价相同的时候,这时两人中标的概率各是1/2。所以用概率乘以中标之后的得益就是第二个分段表达的意思。
而当我们的报价没有对方高的时候就一定不会中标,这时得益为0.
如果战略组合 [ b 1 ( v 1 ) , b 2 ( v 2 ) ] [b_1(v_1),b_2(v_2)] [b1(v1),b2(v2)]是一个贝叶斯纳什均衡,则必须对每个参与人 i i i的每个类型, b i ( v i ) b_i(v_i) bi(vi)都满足期望收益最大化:(贝叶斯纳什均衡是期望收益最大化对应的那个行动)
max b i [ ( v i − b i ) P { b i > b j } + 1 2 ( v i − b i ) P { b i = b j } ] \max _{b_i}\left[\left(v_i-b_i\right) P\left\{b_i>b_j\right\}+\frac{1}{2}\left(v_i-b_i\right) P\left\{b_i=b_j\right\}\right] bimax[(vi−bi)P{
bi>bj}+21(vi−bi)P{
bi=bj}]
那我们如何来求b呢?
- 设 b 1 ( v 1 ) , b 2 ( v 2 ) b_1(v_1),b_2(v_2) b1(v1),b2(v2)是线性函数:
b 1 ( v 1 ) = a 1 + c 1 v 1 b_1(v_1)=a_1+c_1v_1 b1(v1)=a1+c1v1 , b 2 ( v 2 ) = a 2 + c 2 v 2 b_2(v_2)= a_2+c_2v_2 b2(v2)=a2+c2v2
- 其中 a 1 , a 2 < 1 ,可以想成是底价, c 1 , c 2 ≥ 0 a_1,a_2<1,可以想成是底价,c_1,c_2≥0 a1,a2<1,可以想成是底价,c1,c2≥0。设参与人 j j j的战略为:
b j ( v j ) = a j + c j v j b_j(v _j)=a_j+ c_jv_j bj(vj)=aj+cjvj
- 则对任意给定的 v j v_j vj,参与人 i i i的最佳反应 b i b_i bi应满足: b I > b j b_I>b_j bI>bj,那就应该满足: b i > a j + c j v j b_i>a_j+c_jv_j bi>aj+cjvj,则化简过后就应该满足: v j < b i − a j c j v_j<\frac{b_i-a_j}{c_j} vj<cjbi−aj:
max b i [ ( v i − b i ) P { b i > a j + c j v j } ] = max b i [ ( v i − b i ) P { v j < b i − a j c j } ] = max b i [ ( v i − b i ) b i − a j c j ] \max _{b_i}\left[\left(v_i-b_i\right) P\left\{b_i>a_j+c_j v_j\right\}\right]=\max _{b_i}\left[\left(v_i-b_i\right) P\left\{v_j<\frac{b_i-a_j}{c_j}\right\}\right]=\max _{b_i}\left[\left(v_i-b_i\right) \frac{b_i-a_j}{c_j}\right] bimax[(vi−bi)P{
bi>aj+cjvj}]=bimax[(vi−bi)P{
vj<cjbi−aj}]=bimax[(vi−bi)cjbi−aj]
上面由于v是属于 [ 0 , 1 ] [0,1] [0,1]的,所以 P { v j < b i − a j c j } P\left\{v_j<\frac{b_i-a_j}{c_j}\right\} P{
vj<cjbi−aj}就等于线段的长度: v j < b i − a j c j v_j<\frac{b_i-a_j}{c_j} vj<cjbi−aj。
其一阶条件为:
b i ( v i ) = { ( v i + a j ) / 2 if v i ≥ a j a j if v i < a j b_i\left(v_i\right)=\left\{\begin{array}{cl} \left(v_i+a_j\right) / 2 \quad \text { if } v_i \geq a_j \\ a_j \quad\quad\quad\quad\quad\text { if } \mathrm{v}_{\mathrm{i}}<\mathrm{a}_{\mathrm{j}} \end{array}\right. bi(vi)={
(vi+aj)/2 if vi≥ajaj if vi<aj
上面这个式子之所以还分段了,是因为第一部分就是正常令导数为0的时候求得的值,但是这个值尽可能发生在参与人i对商品的估价是大于等于对方的底价的时候,我的估价取这个值才是有意义的。但是如果参与人i的估价连对方的底价都够不着,那么实际上参与人i的估价就没有任何实际意义了,因为肯定不可能中标,所以这时候就干脆估一个对方的底价就行了,因为肯定不会中标。
通过上面的讨论我们发现最优行动是一个分段函数,他有两个部分。但是我们一开始假设的 b i b_i bi是一个线性函数。线性函数严格来说不应该是分段函数,而应该是 y = k x + b y=kx+b y=kx+b这种形式的函数。
所以我们设的是一个线性函数,现在推断出来是一个分段函数,那因此我们为了与一开始设置的线性函数这个出发点保持一致,下面我们就让 a j < = 0 a_j<=0 aj<=0就可以让这个分段函数整合为一个完整的线性函数了。而 a j < = 0 a_j<=0 aj<=0但是 a j a_j aj同时他的物理意义是参与人j的估价的底价,因此同时也是大于等于0的,所以 a j a_j aj就只能等于0.
所以整个的 b i b_i bi的表达式就应该是这一部分了:
b i = v i + a j 2 b_i=\frac{v_i+a_j}{2} bi=2vi+aj
上面是推出的一般表达式,现在将 i = 1 i=1 i=1带入该式子,然后与一开始i我们假设的 b 1 b_1 b1表达式相匹配即可。代入 i = 1 , j = 2 i=1,j=2 i=1,j=2得到:
b 1 = v 1 + a 2 2 b_1=\frac{v_1+a_2}{2} b1=2v1+a2
与原来的假设的式子:
b 1 ( v 1 ) = a 1 + c 1 v 1 b_1(v_1)=a_1+c_1v_1 b1(v1)=a1+c1v1
相比可以得到:
a 1 = a 2 2 , c 1 = 1 2 a_1=\frac{a_2}{2}, c_1=\frac{1}{2} a1=2a2,c1=21
那么根据对称性也有:
a 2 = a 1 2 , c 2 = 1 2 a_2=\frac{a_1}{2}, c_2=\frac{1}{2} a2=2a1,c2=21
又由于我们说对于 b i b_i bi来说,应该让 a j a_j aj等于0,所以再根据对称性,此处的 a i = a j = 0 , c i = c j = 1 2 a_i=a_j=0, c_i=c_j=\frac{1}{2} ai=aj=0,ci=cj=21
所以可以得到最终 b i b_i bi的最终形式如下:
b i ( v i ) = v i / 2 , i = 1 , 2 b_i\left(v_i\right)=v_i / 2, i=1,2 bi(vi)=vi/2,i=1,2
其物理意义是:参与人 i i i觉得某物价值 v i v_i vi元的时候,最佳的叫价策略是只报 v i / 2 v_i / 2 vi/2。
【例3】双方叫价拍卖
Chatterjee and Samuelson ( 1983):设买方和卖方就某货物进行交易,买方对货物的估价为 V b V_b Vb,卖方的估价为 V s V_s Vs,并设 V b V_b Vb和 V s V_s Vs是 [ 0 , 1 ] [0,1] [0,1]上的独立标准分布,且是相互都知道的。交易规则如下:买方和卖方同时各报一个价格,设买方的报价为 P b P_b Pb,卖方的报价为 P s P_s Ps如果 P b ≥ P s P_b≥ P_s Pb≥Ps,则以的价格 ( P b + P s ) / 2 (P_b+ P_s)/2 (Pb+Ps)/2成交,否则不成交。如果双方以价格 Р Р Р成交,则买方的得益为 V b − P V_b-P Vb−P,卖方的得益为 P − V s P-V_s P−Vs如果因价格不合适没有成交,则双方得益均为0。
【解】
首先一定要明确的一点是,题目中说的买方和卖方对对方的情况都知道,说的是只知道对方的估价的标准概率分布,而不是准确的多少。因为这时不完全信息静态博弈。
(1)一价均衡(只有在市场均衡价这一种价格才能成交,别的价格都不可能成交)
- 给定 [ 0 , 1 ] [0,1] [0,1]中任意 X X X,令买方的战略为当 V b ≥ X V_b≥X Vb≥X时, P b = X P_b= X Pb=X,否则 P b = 0 P_b=0 Pb=0。同时令卖方的战略为当 V s ≤ X V_s≤X Vs≤X时, P s = X P_s= X Ps=X,否则 P s = 1 P_s= 1 Ps=1。(这个策略的意思就是参与人心中有一个默认的价值衡量,如果实际参与人对该物品的估价 V b V_b Vb大于该物品的定价,那么参与人会觉得赚了,因此会购买该商品。如果参与人对该物品的估价小于该物品的实际价格,参会人会觉得买它就亏了,因此就不会进行购买。)
可以更进一步理解为,买方觉得这个东西不错,会愿意以市场价格来购买。
卖方觉得这个东西不是太好,就会愿意以市场价格来出售,
如果卖方觉得自己的东西比市场的东西都好,就会要价非常高,所以X可以看作一个参考的价格或者说市场上同类商品的平均价格。
这个就称之为一价均衡,就是只有一个价格会成交。
而且要么成交要么不成交。
那么这个战略能否构成纳什均衡,我们就用纳什均衡来求解一下(纳什均衡就是双方对对方都是最优反应,判断是否能构成纳什均衡就是判定是否真的是最优反应):
- 给定买方的战略,在有可能成交的情况下,即 V s ≤ X ≤ V b V_s≤X≤V_b Vs≤X≤Vb时, P s = X P_s= X Ps=X是卖方能实现的最高要价,任何 P s > X P_s>X Ps>X都不可能成交,因为成交的得益 P − V s = X − V s ≥ 0 P-V_s =X-V_s≥0 P−Vs=X−Vs≥0,因此要价 P s = X P_s=X Ps=X以求成交是最佳反应。而在 V s > X V_s>X Vs>X的情况下,要价 P s = X P_s=X Ps=X成交的得益 P − V s = X − V s < 0 P-Vs =X-V_s<0 P−Vs=X−Vs<0,因此干脆要价 P s = 1 P_s=1 Ps=1 ,不成交至少能避免损失。因此,卖方的战略是对买方战略的最佳反应。
当卖方对货物的估计价值不超过X(也就是卖家觉得自己的货物其实不值X这么多钱,所以如果按照X卖出的话是赚钱的),买方对货物的估计价值不高于X时,高于X是无法成交的。此时成交之后的得益是成交价减去成本,是非负的。
但是如果卖家对X的估价高于X,此时仍然成交的话,可以算出来他的得益是负的,所以此时还不如干脆要加1元,不成交是最划算的选择。
那么上面这两个选择都是卖方对买方的最优战略。
- 同理可证明给定卖方的战略,买方的上述战略也是最佳反应。
用图形看就是这样的:

根据刚才的分析,只有当买方对货物的估计价值大于X,卖方对货物的估计价值小于X的时候,这样的区域中才可能成交。
图中的A点意味着 V s V_s Vs与 V b V_b Vb都等于X且以X的价格成交。那么成交过后卖方和买方有没有新增价值呢?
V s = X V_s=X Vs=X,意味着我得到的货币收益是X,失去的货物利益是X,所以两个相减之后是没有新增价值的。买方也是一样的,失去了价值为X的货币,得到了价值为X的货物,也没有产生任何新增价值。所以该点的交易并没有对双方带来新的价值,只是一个简单的价值交换。该点称之为是一个最无效的交易。
而B点呢,是买方认为货物价值是1(也就是无穷大),而卖方认为货物价值是0。此时如果交易成功,则交易价格应该是 ( P b + P s ) / 2 (P_b+ P_s)/2 (Pb+Ps)/2,也就是1/2(此处仍用X表示)。则交易过后买方的收益是 1 − X 1-X 1−X,卖方觉得一文不值,但是他还卖了X的价格,所以他的收益是净收益X。所以两者认为的价值增益相加:1-X+X,所以这个交易让两者共同增加了1的收益,是对整个社会最有利的交易。
(2)线性均衡
设买方的战略为 P b ( V b ) = a b + c b v b , P_b(V_b)=a_b+c_bv_b, Pb(Vb)=ab+cbvb,设卖方的战略为 P s ( V s ) = a s + c s v s P_s(V_s)=a_s+c_sv_s Ps(Vs)=as+csvs。
如果 [ P b , P s ] [P_b,P_s] [Pb,Ps]是贝叶斯纳什均衡,则对任意的 V b , P b V_b,P_b Vb,Pb必须满足:
max P b [ V b − P b + E [ P s ∣ P b ≥ P s ] 2 ] P { P b ≥ P s } max P s [ P s + E [ P b ∣ P b ≥ P s ] 2 − V s ] P { P b ≥ P s } \begin{aligned} & \max _{P_b}\left[V_b-\frac{P_b+E\left[P_s \mid P_b \geq P_s\right]}{2}\right] P\left\{P_b \geq P_s\right\} \\ & \max _{P_s}\left[\frac{P_s+E\left[P_b \mid P_b \geq P_s\right]}{2}-V_s\right] P\left\{P_b \geq P_s\right\} \end{aligned} Pbmax[Vb−2Pb+E[Ps∣Pb≥Ps]]P{
Pb≥Ps}Psmax[2Ps+E[Pb∣Pb≥Ps]−Vs]P{
Pb≥Ps}
·其中 E [ P s ∣ P b ≥ P s ] E[P_s|P_b≥P_s] E[Ps∣Pb≥Ps]是在符合买方的出价大于卖方的要价的前提下,买方期望卖方的最低要价。 E [ P b ∣ P b ≥ P s ] E[P_b|P_b≥P_s] E[Pb∣Pb≥Ps]是在买方出价高于卖方要价的前提下,卖方期望买方的最高出价。
E [ P s ∣ P b ≥ P s ] = 1 c s ∫ a s P b x d x P { P b ≥ P s } = 1 c s ∫ a s P b x d x P { P b ≥ a s + c s v s } = 1 c s ∫ a s P b x d x P { v s ≤ P b − a s c s } = 1 2 c s ( P b 2 − a s 2 ) P b − a s c s = P b + a s 2 \begin{aligned} E\left[P_s \mid P_b \geq P_s\right] & =\frac{\frac{1}{c_s} \int_{a_s}^{P_b} x d x}{P\left\{P_b \geq P_s\right\}}=\frac{\frac{1}{c_s} \int_{a_s}^{P_b} x d x}{P\left\{P_b \geq a_s+c_s v_s\right\}} \\ & =\frac{\frac{1}{c_s} \int_{a_s}^{P_b} x d x}{P\left\{v_s \leq \frac{P_b-a_s}{c_s}\right\}}=\frac{\frac{1}{2 c_s}\left(P_b^2-a_s^2\right)}{\frac{P_b-a_s}{c_s}} \\ & =\frac{P_b+a_s}{2} \end{aligned} E[Ps∣Pb≥Ps]=P{
Pb≥Ps}cs1∫asPbxdx=P{
Pb≥as+csvs}cs1∫asPbxdx=P{
vs≤csPb−as}cs1∫asPbxdx=csPb−as2cs1(Pb2−as2)=2Pb+as
将上面的推到结果带入原式可得:
max P b [ V b − 1 2 ( P b + a s + P b 2 ) ] P b − a s c s 将上式对 P b 对微分令其等于 0 可得: P b = 2 3 V b + 1 3 a s a b = a s 3 , c b = 2 3 max P s [ 1 2 ( P s + P s + a b + c b 2 ) − V s ] a b + c b − P s c b 将上式对 P s 对微分令其等于 0 可得: P s = 2 3 V s + 1 3 ( a b + c b ) a s = a b + c b 3 , c s = 2 3 \begin{gathered} \max _{P_b}\left[V_b-\frac{1}{2}\left(P_b+\frac{a_s+P_b}{2}\right)\right] \frac{P_b-a_s}{c_s} \\ 将上式对P_b对微分令其等于0可得:\\ P_b=\frac{2}{3} V_b+\frac{1}{3} a_s \quad a_b=\frac{a_s}{3}, c_b=\frac{2}{3} \\ \max _{P_s}\left[\frac{1}{2}\left(P_s+\frac{P_s+a_b+c_b}{2}\right)-V_s\right] \frac{a_b+c_b-P_s}{c_b}\\ 将上式对P_s对微分令其等于0可得:\\ P_s=\frac{2}{3} V_s+\frac{1}{3}\left(a_b+c_b\right) \quad a_s=\frac{a_b+c_b}{3}, c_s=\frac{2}{3} \\ \end{gathered} Pbmax[Vb−21(Pb+2as+Pb)]csPb−as将上式对Pb对微分令其等于0可得:Pb=32Vb+31asab=3as,cb=32Psmax[21(Ps+2Ps+ab+cb)−Vs]cbab+cb−Ps将上式对Ps对微分令其等于0可得:Ps=32Vs+31(ab+cb)as=3ab+cb,cs=32
{ P b ( V b ) = 2 3 V b + 1 12 P s ( V s ) = 2 3 V s + 1 4 \begin{aligned} & \left\{\begin{array}{l} P_b\left(V_b\right)=\frac{2}{3} V_b+\frac{1}{12} \\ P_s\left(V_s\right)=\frac{2}{3} V_s+\frac{1}{4} \end{array}\right. \\ \end{aligned} {
Pb(Vb)=32Vb+121Ps(Vs)=32Vs+41
最终得到线性均衡下的卖方出价和买方估价的表达式。
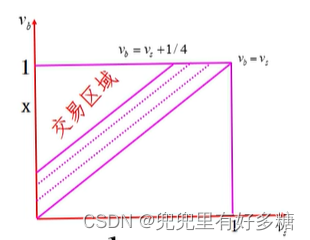
2 3 V b + 1 12 ≥ 2 3 V s + 1 4 V b ≥ V s + 1 4 \begin{aligned} \frac{2}{3} V_b+\frac{1}{12} \geq \frac{2}{3} V_s+\frac{1}{4} \quad V_b \geq V_s+\frac{1}{4} \\ \end{aligned} 32Vb+121≥32Vs+41Vb≥Vs+41
画出图如下:
比较:
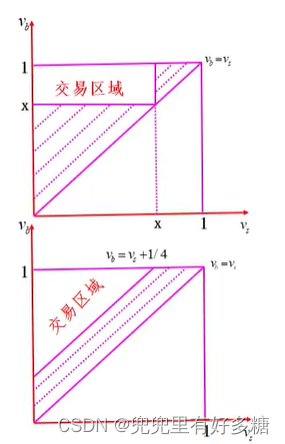
- 线性均衡中交易机会大于一价均衡的交易机会。 双方都包含了最有效率的交易,即 V s = 0 , V b = 1 V_s= 0,V_b= 1 Vs=0,Vb=1。
- 一价均衡排除了许多很有价值的交易,当 V s V_s Vs等干或接近0,而 V b V_b Vb却小于但接近 X X X时,一价均衡中无法交易,但在线性均衡中却能够交易,并且双方的得益是相当可观的,都是接近 X / 2 X/2 X/2。
- V b V_b Vb略大于 X X X, V x V_x Vx略小于 X X X,这种交易实际无多大利益,而线性均衡中是不包括这种交易机会的。
- 线性均衡应该是优于一价。Myerson and Satterhwaite (1983)证明:在估价为标准分布的前提下,在双方报价拍卖静态贝叶斯博弈中,线性均衡能产生比其他任何贝叶斯纳什均衡更高的期望得益。
【例4】不完全信息条件下公共物品提供博弈模型
两个参与人 ( i = 1 , 2 ) (i= 1,2) (i=1,2)同时决定是否提供公共物品, a i = 1 a_i=1 ai=1表示提供, a i = 0 a_i=0 ai=0表示不提供。只要有一个人提供,每人的效用为1;如果没有人提供,每人的效用为0。两个参与人提供公共物品的成本 c 1 c_1 c1与 c 2 c_2 c2,是私人信息,但成本的类型空间 T 1 = T 2 = [ 0 , 2 ] T_1=T_2=[0,2] T1=T2=[0,2]。参与人1认为 c 2 c_2 c2,的概率分布函数为 F ( x ) = x / 2 F(x)=x/2 F(x)=x/2,参与人2认为 c 1 c_1 c1的概率分布函数为 G ( x ) = x 2 / 4 G(x)=x^2/4 G(x)=x2/4,求该博弈的贝叶斯均衡。
【解】
这种的很典型的一个场景就是两家共用一个走廊,灯坏了,谁家会去装灯,只要有一家会把灯换掉,那么两家都会得到效用。但是去换灯是有成本的,这个成本是一个私人信息,自然为每个人抽取的类型就是这个题里面的成本,这个类型的范围就是该题中的灯的成本的取值范围。参与人1对参与人2只能知道他的成本的概率分布,而不知道准确值,而自己是知道自己的准确的成本是多少的。
那期望应该怎么求呢:
就是用原函数乘概率密度函数,然后积分,就是总的期望值,也就是该点的概率值是多少,乘该点的值,再加上下一点的概率乘下一点的值,如果分布是连续的,那么累计就是求其积分,如果分布是离散的,那么累计就是求和。
支付函数就变为了积分形式:
由于题中给的是分布函数,所以对分布函数先求微分得到概率密度函数,然后才能算期望:
c 2 c_2 c2的分布函数是 F ( x ) = x / 2 F(x)=x/2 F(x)=x/2,求微分就是 f ( x ) = 1 / 2 f(x)=1/2 f(x)=1/2,所以 f ( c 2 ) = 1 / 2 f(c_2)=1/2 f(c2)=1/2
c 1 c_1 c1的分布函数是 G ( x ) = x 2 / 4 G(x)=x^2/4 G(x)=x2/4,求微分就是 g ( x ) = x / 2 g(x)=x/2 g(x)=x/2,所以 g ( c 1 ) = c 1 / 2 g(c_1)=c_1/2 g(c1)=c1/2
并且我们考虑自己会不会提供的时候,也会考虑对方会不会提供,当对方提供的成本大于某个值的时候,他就不会提供,小于某个值的时候才可能会提供。所以尽管对方的成本区间是在 [ 0 , 2 ] [0,2] [0,2]范围内的,但实际上他可能提供公共物品的前提肯定是成本在 [ 0 , x ] , x < 2 [0,x],x<2 [0,x],x<2.这个 x x x是某个不为2的值。
比如我们站在参与人1的角度看参与人2,参与人2一定会在小于某个成本 c 2 c_2 c2的时候愿意提供,而大于该值的时候不愿意提供。所以参与人1的策略也要随着这个值改变,分成两段。
最后需要理解的就是下面的收益函数是得到的效益减去付出的成本,所以后面有一个减去的一项。
max c 1 ∈ T 1 ∫ 0 2 ( a 1 , a 2 ∗ ) 1 2 d c 2 − a 1 c 1 = max c 1 ∈ T 1 [ ∫ 0 c 2 ∗ ( a 1 , a 2 ∗ = 1 ) 1 2 d c 2 ∗ 1 + ∫ c 2 ∗ 2 ( a 1 , a 2 ∗ = 0 ) 1 2 d c 2 ∗ 1 ] − a 1 c 1 ( 参与人 2 在提供成本低于 c 2 ∗ 时,会提供,即 a 2 ∗ = 1 ,否则不提供 ) ( 化简 ) = max c 1 ∈ T 1 [ 1 2 c 2 ∗ + a 1 ( 1 − 1 2 c 2 ∗ ) ] − a 1 c 1 (期望效用无差异) ⇒ 1 − c 1 ∗ = c 2 ∗ / 2 \begin{aligned} & \max _{c_1 \in T_1} \int_0^2\left(a_1, a_2^*\right) \frac{1}{2} d c_2-a_1 c_1 \\ & =\max _{c_1 \in T_1}\left[\begin{array}{l} \int_0^{c_2^*}\left(a_1, a_2^*=1\right) \frac{1}{2} d c_2*1 \\ +\int_{c_2^*}^2\left(a_1, a_2^*=0\right) \frac{1}{2} d c_2*1 \end{array}\right]-a_1 c_1 \\ &(参与人2在提供成本低于c_2^*时,会提供,即a_2^*=1,否则不提供)\\ &(化简) =\max _{c_1 \in T_1}\left[\frac{1}{2} c_2^*+a_1\left(1-\frac{1}{2} c_2^*\right)\right]-a_1 c_1 \\ &(期望效用无差异) \Rightarrow 1-c_1^*=c_2^* / 2 \end{aligned} c1∈T1max∫02(a1,a2∗)21dc2−a1c1=c1∈T1max[∫0c2∗(a1,a2∗=1)21dc2∗1+∫c2∗2(a1,a2∗=0)21dc2∗1]−a1c1(参与人2在提供成本低于c2∗时,会提供,即a2∗=1,否则不提供)(化简)=c1∈T1max[21c2∗+a1(1−21c2∗)]−a1c1(期望效用无差异)⇒1−c1∗=c2∗/2
上式表示的就是在给定参与人2的最佳选择 a 2 ∗ a_2^* a2∗的时候参与人1如何根据自己的成本 c 1 c_1 c1来做自己的选择 a 1 a_1 a1,这个式子中 a 1 a_1 a1是决策变量,也就是自变量。
在化简式子: ∫ 0 c 2 ∗ ( a 1 , a 2 ∗ = 1 ) 1 2 d c 2 ∗ 1 \int_0^{c_2^*}\left(a_1, a_2^*=1\right) \frac{1}{2} d c_2*1 ∫0c2∗(a1,a2∗=1)21dc2∗1的时候我们要考虑的就是 a 1 = 0 a_1=0 a1=0的时候该式为多少, a 1 = 1 a_1=1 a1=1的时候该式子为多少。我们讨论之后会发现由于已经有 a 2 = 1 a_2=1 a2=1,所以意味着参与人2已经提供了公共物品,所以此时不论 a 1 a_1 a1是否取1,也就是不论参与人1是否提供该公共物品,他们两人的效用都是1,所以这一项的收益其实是与 a 1 a_1 a1的取值无关的。算出来就等于一个常数 1 2 c 2 ∗ \frac{1}{2} c_2^* 21c2∗,当然,会有成本的讨论,也就是参与人1如果选择提供该公共物品,则会有相应的 c 1 c_1 c1的成本,这个我们统一放在最后一项,此处不予考虑。
但是第二个式子: ∫ c 2 ∗ 2 ( a 1 , a 2 ∗ = 0 ) 1 2 d c 2 ∗ 1 \int_{c_2^*}^2\left(a_1, a_2^*=0\right) \frac{1}{2} d c_2*1 ∫c2∗2(a1,a2∗=0)21dc2∗1的情况不同。该式中参与人2并未选择提供物品,所以参与人1的选择会对最终结果产生影响,当 a 1 = 0 a_1=0 a1=0时,所有人的效用为0,所以该项不存在;当 a 1 = 1 a_1=1 a1=1时,效用为1,积分之后结果是 ( 1 − 1 2 c 2 ∗ ) (1-\frac{1}{2} c_2^*) (1−21c2∗),所以我们把该式子的结果直接写为 a 1 ( 1 − 1 2 c 2 ∗ ) a_1(1-\frac{1}{2} c_2^*) a1(1−21c2∗)。
所以参与人1的收益就被分为了两部分:
如果参与人2提供,那么参与人1获得1的效用收益,如果参与人2不提供,那么还取决于 a 1 a_1 a1的选择,也就是参与人1自己的选择。
所以参与人1的得益算出来之后是一个关于 a 1 a_1 a1的式子,参与人1希望自己提供或者不提供,期望收益值是无差异的,所以就令:
[ 1 2 c 2 ∗ + a 1 ( 1 − 1 2 c 2 ∗ ) ] − a 1 c 1 ∣ a 1 = 0 = [ 1 2 c 2 ∗ + a 1 ( 1 − 1 2 c 2 ∗ ) ] − a 1 c 1 ∣ a 1 = 1 \left[\frac{1}{2} c_2^*+a_1\left(1-\frac{1}{2} c_2^*\right)\right]-a_1 c_1\Bigg|_{a_1=0}=\left[\frac{1}{2} c_2^*+a_1\left(1-\frac{1}{2} c_2^*\right)\right]-a_1 c_1\Bigg|_{a_1=1} [21c2∗+a1(1−21c2∗)]−a1c1
a1=0=[21c2∗+a1(1−21c2∗)]−a1c1
a1=1
下面同理:
max c 2 ∈ T 2 ∫ 0 2 ( a 1 ∗ , a 2 ) c 1 2 d c 1 − a 2 c 2 = max c 2 ∈ T 2 [ ∫ 0 c 1 ∗ ( a 1 ∗ = 1 , a 2 ) c 1 2 d c 1 + ∫ c 1 ∗ 2 ( a 1 ∗ = 0 , a 2 ) c 1 2 d c 1 ] − a 2 c 2 = max c 2 ∈ T 2 [ 1 4 ( c 1 ∗ ) 2 + a 2 × ( 1 − 1 4 ( c 1 ∗ ) 2 ) ] − a 2 c 2 ⇒ 1 − c 2 ∗ = 1 4 ( c 1 ∗ ) 2 \begin{aligned} & \max _{c_2 \in T_2} \int_0^2\left(a_1^*, a_2\right) \frac{c_1}{2} d c_1-a_2 c_2 \\ & =\max _{c_2 \in T_2}\left[\begin{array}{l} \int_0^{c_1^*}\left(a_1^*=1, a_2\right) \frac{c_1}{2} d c_1+ \\ \int_{c_1^*}^2\left(a_1^*=0, a_2\right) \frac{c_1}{2} d c_1 \end{array}\right] -a_2 c_2\\ & =\max _{c_2 \in T_2}\left[\frac{1}{4}\left(c_1^*\right)^2+a_2 \times\left(1-\frac{1}{4}\left(c_1^*\right)^2\right)\right]-a_2 c_2 \\ & \Rightarrow 1-c_2^*=\frac{1}{4}\left(c_1^*\right)^2 \\ & \end{aligned} c2∈T2max∫02(a1∗,a2)2c1dc1−a2c2=c2∈T2max[∫0c1∗(a1∗=1,a2)2c1dc1+∫c1∗2(a1∗=0,a2)2c1dc1]−a2c2=c2∈T2max[41(c1∗)2+a2×(1−41(c1∗)2)]−a2c2⇒1−c2∗=41(c1∗)2
则最后联立两个参与人的最优选择可以得到:
1 − c 1 ∗ = 1 2 c 2 ∗ 1 − c 2 ∗ = 1 4 ( c 1 ∗ ) 2 } ⇒ { c 1 ∗ = 4 − 2 3 c 2 ∗ = 4 3 − 6 a ∗ = { a 1 ∗ ( T 11 ) = 1 , a 1 ∗ ( T 12 ) = 0 ; a 2 ∗ ( T 21 ) = 1 , a 2 ∗ ( T 22 ) = 0 } T 11 = [ 0 , c 1 ∗ ] , T 12 = [ c 1 ∗ , 2 ] , T 21 = [ 0 , c 2 ∗ ] , T 22 = [ c 2 ∗ , 2 ] \begin{aligned} &\left.\begin{array}{l} 1-c_1^*=\frac{1}{2} c_2^* \\ 1-c_2^*=\frac{1}{4}\left(c_1^*\right)^2 \end{array}\right\} \Rightarrow\left\{\begin{array}{l} c_1^*=4-2 \sqrt{3} \\ c_2^*=4 \sqrt{3}-6 \end{array}\right.\\ &\begin{aligned} & a^*=\left\{a_1^*\left(T_{11}\right)=1, a_1^*\left(T_{12}\right)=0 ; a_2^*\left(T_{21}\right)=1, a_2^*\left(T_{22}\right)=0\right\} \\ & T_{11}=\left[0, c_1^*\right], T_{12}=\left[c_1^*, 2\right], T_{21}=\left[0, c_2^*\right], T_{22}=\left[c_2^*, 2\right] \end{aligned} \end{aligned} 1−c1∗=21c2∗1−c2∗=41(c1∗)2}⇒{
c1∗=4−23c2∗=43−6a∗={
a1∗(T11)=1,a1∗(T12)=0;a2∗(T21)=1,a2∗(T22)=0}T11=[0,c1∗],T12=[c1∗,2],T21=[0,c2∗],T22=[c2∗,2]
三、机制设计
1.拍卖规则的设计问题(要尽可能地促进交易人投标):
- 投标人较少可能会出价极低
- 投标无成本的可能不会积极争取成交
- 侥幸赚到大便宜
- 避免方法:预先设置底价、定金
2.“鼓励-响应”的“直接机制(direct mechanism) ”
- 投标人同时声明自己对货物的估价。
- 假如各投标人的声明是 ( t 1 , … , t n ′ ) (t_1,…,t'_n) (t1,…,tn′),则投标方 i i i拍得货物的概率为 q i ( t 1 ′ … , t n ′ ) q_i(t_1'…,t_n') qi(t1′…,tn′)。如果投标方 i i i中标,则价格为 p i ( t 1 ′ … , t n ′ ) p_i(t_1'… ,t_n') pi(t1′…,tn′).对各种可能声明情况 ( t 1 , … , t n ′ ) (t_1,…,t'_n) (t1,…,tn′),概率之和满足: q 1 ( t 1 ′ … , t n ′ ) + . . . . . . + q n ( t 1 ′ … , t n ′ ) = 1 q_1(t_1'…,t_n')+......+q_n(t_1'…,t_n')=1 q1(t1′…,tn′)+......+qn(t1′…,tn′)=1
- 这种规则称为“直接机制”。如果所设计的直接机制能使得各投标人讲真话为贝叶斯纳什均衡,则称这个直接机制为“鼓励─响应”的。
我们希望参与人说真话,也就是它是什么的类型就说什么样的类型,就是直接机制。所以这个机制就是鼓励参与人说真话,并且参与人也确实是如此响应的,所以该模型叫做“鼓励响应机制”。
我们希望他声明的这个货物估计价值就是他真是认为的货物的估计价值。上面我们设置个参与人的声明价格为 t i t_i ti,我们希望这个声明价格就是他最后的真实的估计。那么他拍得的这个货物的概率是关于你声明的价格的函数,并且中标过后不是你声明的 t i t_i ti值,而是关于所有投标人声明价格的一个函数。
所以想要设计好这个鼓励模型就是主要就是设计最后中标的价格和中标的概率,这两个设计好了就可以促进参与人形成说真话的激励。
【例题】
设只有两个投标人,他们的估价类型都是 [ 0 , 1 ] [0,1] [0,1]上的标准分布。
- 两投标人同时声明 V 1 ′ , V 2 ′ V_1',V_2' V1′,V2′。假设声明为线性齐次,即 V i ′ = a i V i V_i' = a_iV_i Vi′=aiVi.
- 投标人 i i i中标的概率为 q i = V i ′ / 2 q_i=V_i'/2 qi=Vi′/2, 中标的价格为 p i = V i ′ / θ p_i=V_i'/\theta pi=Vi′/θ
【解】
V i ′ V_i' Vi′就是最后参与人声明的价格, V i V_i Vi是参与人本身认为该货物的应该估价。我们要做的就是尽可能使得 V i ′ V_i' Vi′等于 V i V_i Vi,也就是尽量使 a = 1 a=1 a=1。
可以看到第二个条件很好的限制了 p p p的概率不大于1,因为 V i ′ V_i' Vi′取值都在0到1之间,所以两个参与人的概率加起来也不会大于1。
中标的价格初步把它定为声明价格除以一个常系数 θ \theta θ,所以现在我们就是要分析为了使得 a = 1 a=1 a=1,如何设计 θ \theta θ。
如何设计 θ \theta θ我们就要考虑投标人怎么想,投标人肯定是期望投标过后的期望收益最大,期望收益一共有两部分,一个是投标未中,一个是中标。
中标的收益值还取决于中标的概率。
投标人 i i i声明的期望收益是;
E u i = V i ′ 2 × ( V i − V i ′ θ ) = a i V i 2 ( V i − a i V i θ ) E u_i=\frac{V_i^{\prime}}{2} \times\left(V_i-\frac{V_i^{\prime}}{\theta}\right)=\frac{a_i V_i}{2}\left(V_i-\frac{a_i V_i}{\theta}\right) Eui=2Vi′×(Vi−θVi′)=2aiVi(Vi−θaiVi)
对投标人 i i i来说,均衡条件是找出使得期望收益取得最大值:
max a i a i V i 2 ( V i − a i V i θ ) = V i 2 2 θ ( a i θ − a i 2 ) \max _{a_i} \frac{a_i V_i}{2}\left(V_i-\frac{a_i V_i}{\theta}\right)=\frac{V_i^2}{2 \theta}\left(a_i \theta-a_i^2\right) aimax2aiVi(Vi−θaiVi)=2θVi2(aiθ−ai2)
那么这个期望收益我们是对谁求极大值?
其实决策变量应该是 a a a。
所以关于 a a a的一阶条件: a i = θ / 2 a_i=\theta/2 ai=θ/2。
所谓投标人 i i i说真话,即: θ = 2 , a i = 1 , V i = V i ′ \theta=2,a_i=1,V_i=V_i' θ=2,ai=1,Vi=Vi′。此时中标价格为中标人声明估价的一半。
四、揭示原理:
揭示原理(revelation principle; Myerson,1979 ) :任何贝叶斯博弈的任何贝叶斯纳什均衡都可以被一个“鼓励-响应”的直接机制“代表”。(大白话:这种贝叶斯均衡肯定是存在的,问题就在于如何去设计去达到这样的均衡)