目录
1.4 张量(tensor)：标量，向量，矩阵都可以看成张量
2.1 转：插播一个数学里其他概念的辨析：群，环，域，集合，空间的定义（表示不懂，只是做个标记）
2.3 向量空间（vector space 或者线性空间 linear space）
1 标量和向量
1.1 标量 scalar
标量 scalar，就是一个单独的数！标量还有一种更深刻的说法，就是线性变换时不会发生变化的量. 数有很多种：
- 自然数
- 整数（正负）
- 有理数（包含整数，无限循环小数 or =整数/整数）
- 实数（包含有理数和无理数）
- 复数（包含实数和虚数）
1.2 向量vector /矢量
- 向量vector也叫矢量，表示一组n个数构成的有序排列的数
- 向量也可以认为就是 数组list，比如[1,2,3,4,5]
- 在各种向量空间里的二维图，三维图里，就是空间里的点（其终点代表了从原点出发的向量）
- 向量，可以认为是带方向的，方向就是 数组里的数字的排序
- 向量可以对应很多语言里的数组list，比如[1,2,3,4,5]
- 竖着的叫列向量， α={x1,x2,x3....xn}
- 横着的为行向量， αT={x1,x2,x3....xn}
1.2.1 什么是向量
- 向量就是一组数字，而不是一个单个数字，α={x1,x2,x3....xn}
1.2.2 向量如何表示？在向量空间的表示方法
- 在一般的向量空间，向量是指从原点出发的一条射线线段
- 线段起点一定是原点，线段终点是向量的内容(x1,x2) 或（x1,x2,x3）或其他，这同时也是向量在这个向量空间的坐标
因此这种向量空间特点是
- 向量空间一定有原点
- 每个向量都是从原点出发的射线线段，用终点坐标即可代表向量
- 不存在2个向量平行的关系，最多是2个向量在同一条直线上
1.3 矩阵(matrix)
- 矩阵是一个二维数组，其中的每一个元素由两个索引来决定 A(i,j)
- 很多编程语言里把每1行看成1个对象，每1列看成属性/特征
- 可以说，矩阵就是2维数组
- 矩阵A(i,j) 比如 ( a11,a12 ; a21,a22 )
1.3.1 矩阵和向量的关系
观点1
- 基础观点
- 矩阵是由多个向量构成的，一般认为是多个列向量（基）构成的
- 矩阵就是一个在N维度空间里的坐标，这个坐标包含多个向量
观点2
- 计算时,可以认为向量就是一种特殊的矩阵
- 列向量就是列矩阵
- 行向量就是行矩阵
1.3.2 方阵
- 矩阵里，行数=列数的矩阵叫做方阵
- 方阵有很多很好的特殊属性
1.4 张量(tensor)：标量，向量，矩阵都可以看成张量
- 可以说，张量就是2维数组
- 矩阵A(i,j,k) 比如 ( a11,a12 ; a21,a22 ; a31,a32 )
- 张量的定义
- 一个数字的标量，称为0阶张量
- 一个数组的这种向量，(1,2)，称为1阶张量 （相当于1个维度）
- 2个数组的这种矩阵，比如(1,2;1,1)，称为2阶张量 （相当于2个维度）
- 超过二维的数组，如一个三维的A(i,j,k)，就称为3阶张量
1.5 举例子说明
- 注意写法：
- 数量→逗号 一个维度的数量
- 维度→分号; 分隔不同的维度
- 标量：1，5，11，101，999等等
- 向量
- 1维向量 (0,1,2) 或 (1,2,3...... 1001)
- 2维向量 (0,1,2; 3,4,5) 或 [[0,1,2]; [3,4,5]] 或 [ [1,2,3...... 1001] , [1,2] ]
- 张量
- 3维向量--标量 [ [1,0,0] [0,1,0] [0,0,1] ]
下面用的是网上的2张图，不是我自己的
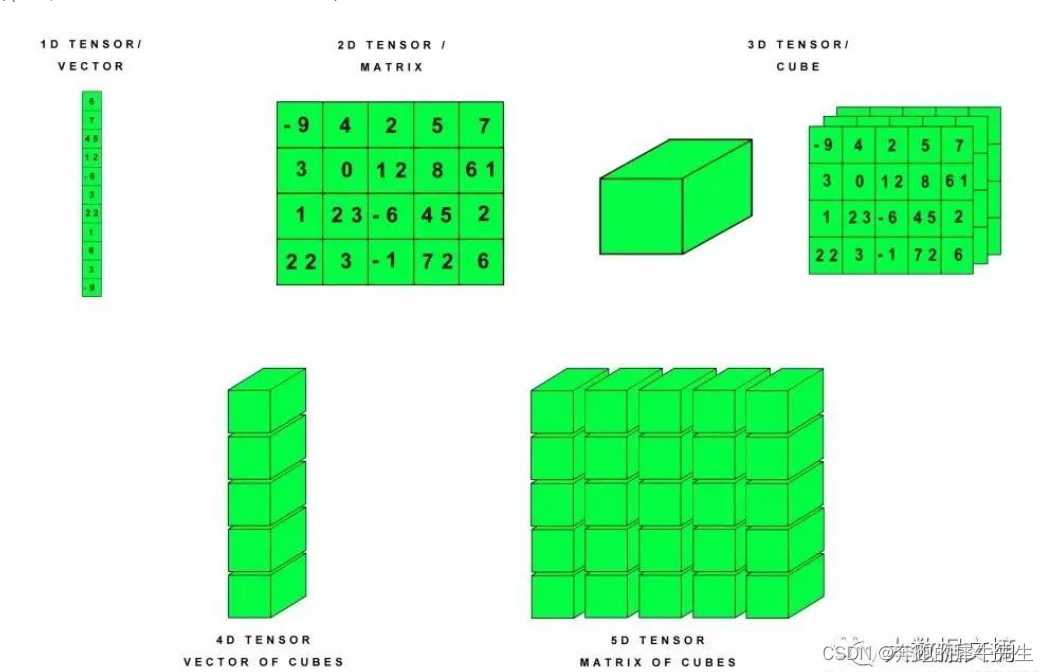
1.6 下面几个例子（一般仍然存在争议？--可以灵活选择处理方法）
- 下表仍然是一个表现上是1个2维表，其实也可以看成N维的张量？
- 可以灵活设计，做成2维的，或者3维度的都可以，因为可以选择把一部分属性，合并成同一个维度
| 价格 | 数量 | 颜色 | 重量 | 尺寸 | |
| A | 10 | 5 | red | 10 | 5 |
| B | 50 | 2 | blue | 3 | 2 |
| C | 100 | 1 | yellow | 1 | 1 |
| D | 30 | 10 | green | 5 | 3 |
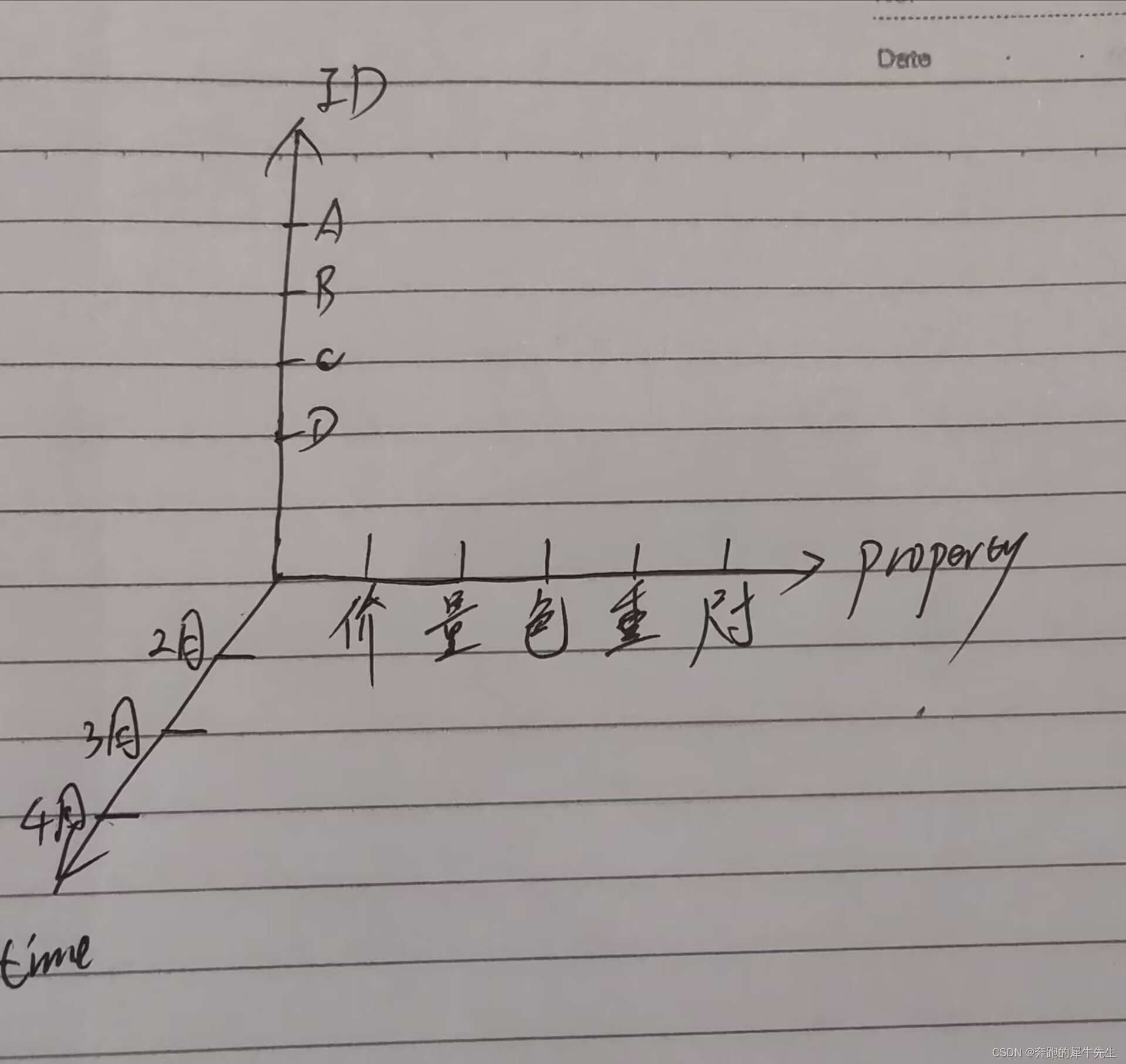
- 而这个才算张量？
- 3个坐标轴
- 如果把 time 看作Z轴。
- 那么x为ID，y为property 意味着，ID-价格，ID-数量，ID-颜色，，，，可以组成N张二维表，这些二维表可以叠在一起。形成了Z轴？
- 可以灵活设计，做成2维的，或者3维度的都可以，因为可以选择把一部分属性，合并成同一个维度
- 维度1的 价格，数量，颜色，重量，尺寸等可以看作一个维度，做成1个三维坐标轴。也可以展开为多个维度，看具体的处理数据的需要
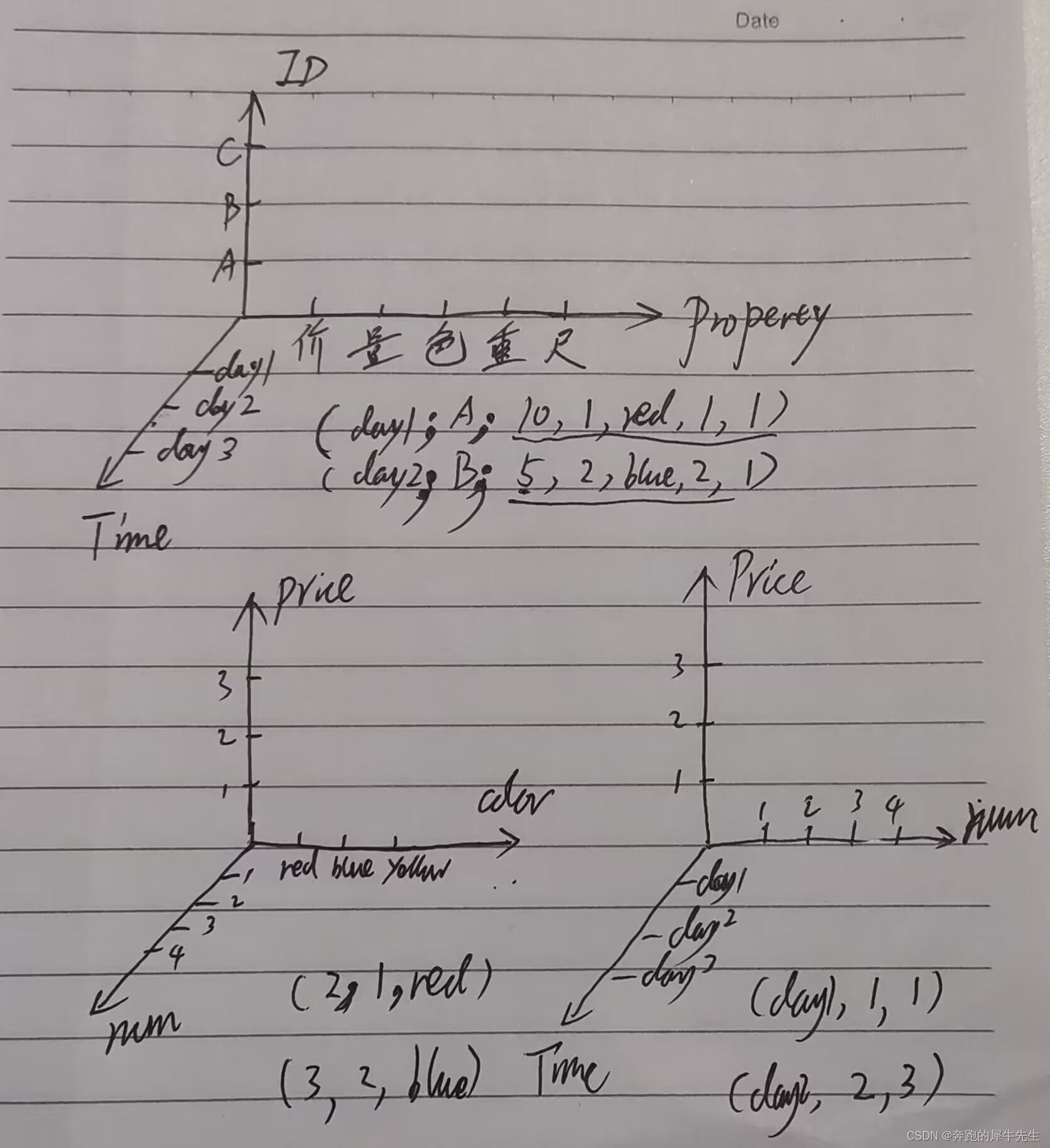
1.7 更多维度的张量，举例子
- 3维=时间序列
- 4维=图像
- 5维=视频
2 什么是向量空间，向量的张成空间？
说空间，先需要从更复杂的概念入手
2.1 转：插播一个数学里其他概念的辨析：群，环，域，集合，空间的定义（表示不懂，只是做个标记）
- 这部分内容是摘抄
- 集：集合可以理解为一些对象的无序的集合体
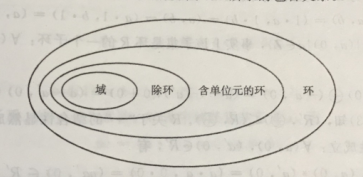
- 群：群是一种具有特定运算和性质的集合，群是在集合的基础上引入了一个二元运算（如加法或乘法），并满足封闭性、结合律、单位元和逆元这四个性质，可以理解为任意两个元素的和还在群内，就叫作群。群只有一种加法运算？
- 环：最早指的是整数环，后来环又被称为代数，成为了代数学的标准对象。环是在群的基础上加入了另一种运算，并满足一定性质。因此，环是对群概念的扩展和加强。环是一种代数结构，包含两个运算，通常为加法和乘法。环需要满足加法构成群、乘法满足封闭性、结合律、分配律。
- 域：域是一个非常抽象的概念，域暗示了一种足够大的概念，在代数学里它能够作加减乘除运算，在数理逻辑里把函数有定义的集合称作定义域，取值的范围称作值域，在模型论里把所有数学对象构成的集合称作论域。域曾经被称为体。域在环的基础上要求乘法（除去乘法单位元外的元素）也构成一个交换群，即乘法需要满足交换律、单位元和逆元的性质。简言之，域是满足更严格性质的环。因此，域是对环概念的扩展和加强。
- 空间：可见空间跟这些深奥概念也是有关系的
数学中的群、域、环三者的严格数学定义是什么？ - 知乎在集合 上定义一个二元运算 ，把它称为加法 。现在有一下这些法则：1）结合律：对于任意 有 2）存在…
https://www.zhihu.com/question/449089514/answer/1777658855数学【1】关于群、环、域、模 - 知乎读起来可能会有一点点乱，也可能会有一些语法上的奇怪，不要在意……引入-自然数集合先来说说自然数，不引用它的精确定义，先快速解释一波：“所有大于0的整数被称为自然数。（这里0不认为是自然数）” 那么将所有…https://zhuanlan.zhihu.com/p/336562401?utm_id=0
2.2 标量空间
- 只有单个的数字等标量
- 包含多个标量
- 标量的加减乘除等也表现为封闭性
- 标量集合中的任何两个标量都可以经过加法和乘法这两种运算得到另一个标量。如果这两种运算满足封闭性、结合律、交换律和对逆元素的要求，那么这些标量就构成了一个标量场。我们熟悉的标量有实数、复数和有理函数等。
2.3 向量空间（vector space 或者线性空间 linear space）
- 首先线性空间中有标量和向量两种个对象
- 是最重要的数学空间。向量空间中包含了两种不同的实体---向量和标量。除了两个标量之间的运算外，向量空间中还定义了标量---向量乘法和向量---向量加法。
- 向量空间，从做图上可以看出，无论是2维还是3维的向量空间，都是从原点除法的射线线段，终点坐标可以代表这个向量''
2.3.1 线性空间定义
线性空间指的是，有一个集合由被称为“向量”的“定长坐标序列”凑到一块组成，然后在这个集合中向量之间，定义上两种运算“加法”和“数乘”，二者合起来(所组成的代数结构) 称为线性空间，当然，还有一点额外要求，那就是封闭性：该集合中的任意向量都可以合法地执行这两种运算，结果还在这个集合里。
如果非封闭性，数学家们觉得不如把新算出来的那个玩意也包含到已有的研究对象里来，毕竟本来也是想研究“所有同类”。所以要求这个封闭性。
- 向量组成的一个集合
- 这个集合，以及定义在这个集合上的代数运算，就是线性空间
- 这个线性空间对标了普通的单个数字运算的一般 整数和函数的那个运算空间
2.4 仿射空间（affine space）
- 而仿射空间与线性空间的区别就在于，它又加了一个对象，这个对象就是“点”。
- 包含：点，标量，向量这3种对象
- 并且它们在运算规则上也不相同。
-
仿射空间它是向量空间的扩展，除了标量和向量外，它还包含了另外一种对象---点。尽管在仿射空间中队两个点以及一个标量没有定义运算，但对一个向量和一个点定义了一种运算---向量-点加法，它的结果是一个点。也可以说有一种称为点---点减法的运算，这种运算由两个点得到一个向量。
或者可以这样理解：仿射空间是假设我们已经定义好了向量空间，然后定义一个点的集合，同时规定了点和向量之间的求和运算（加和的结果仍是搜索点），这个点集就是这个向量空间相伴的仿射空间。
仿射空间和线性空间的区别
- 线性空间必须满足加法和数乘运算的封闭性，即对于任意向量u,v和标量a,b，u+v和au+bv都必须属于线性空间。
- 仿射空间只需要满足向量之间可以相减，并且可以对向量进行加减运算，不必满足数乘运算的封闭性。
- 线性空间中存在一个零向量，即加上它不改变向量的值。
- 仿射空间中没有零向量的概念。
- 线性空间中的向量有大小和方向的概念，可以进行数量的比较。
- 仿射空间中的向量只有方向的概念，没有大小的概念。
- 线性空间中的向量可以用坐标系表示，向量的坐标具有唯一性，也就是终点终点。
- 仿射空间中的向量不能用坐标系表示，只能用向量之间的关系表示。
- 线性空间中的向量空间是一个线性子空间，即它的子集也满足线性空间的条件。
- 仿射空间中的仿射空间不是一个仿射子空间，它的子集也不必满足仿射空间的条件。
2.5 欧几里得空间（Euclidean space）
- 仿射空间相当于欧几里得空间去除了距离（保留长度比）和夹角的概念，只保留了直线、直线平行和平行直线上的长度比
- 欧式空间是指坐标空间中（坐标的每一个分量是定义在域上的），规定了坐标的加法和数乘（到这里，称为向量空间），（注意下面这个才是关键！）并定义了坐标之间的内积。定义了内积后，就可以规定空间中不同坐标之间的距离和它们方向的夹角了，具备了欧式几何学所需的几何结构了。
3 向量空间：就是向量的 张成空间
3.1 向量空间的定义
- 简而言之：向量空间，就是向量的张成空间
- 就是指定向量的所有线性组合的结果组成的张成空间
先有“线性组合” 这个概念
- 一组线性无关的向量（基）的所有线性组合，组成的新的向量（坐标），他们全部构成的空间称为向量的张成空间。
- 比如某向量组{v1,v2...vn} 可以是2个，3个或更多
- 但是一般是2个向量组--组成XOY平面，而3个向量组组成XOYOZ空间
- V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
- 也就是某向量组{v1,v2...vn} 进行任意线性组合（加法和标量乘法），其结果仍然在向量空间内，这就是封闭性，所以。
加法和数乘的封闭性
- 先线性组合概念 --代表了一种计算结果的封闭性，还在这个空间之内
- 线性空间满足两个“运算封闭性”，对所定义的“加法”和“数乘”，假设 α 和 β 是从空间里随便拿出来的两个，则：
- γ=α+β 也在空间里(集合中)
- η=kα 也在空间里(集合中)
3.2 线性相关，专门说过了
注意这里，α1是一个数组/向量，而不是数组里的一个具体的数字,比如α1={x1,x2......}
(线性代数矩阵等肯定是研究 数组/向量之间的关系，而绝不是单个数字之间的关系)
如果 A中的多个向量：α1, α2, α3, .....αn ，如果存在不全部为0的一组实数k1,k2,k3....kn，可以使得k1*α1+ k2*α2+...+ kn*αn=0 ,
那么这些向量 α1, α2, α3, α4, .....αn就是线性相关的
3.3 线性组合的意思
- 比如某向量组{v1,v2...vn} 可以是2个，3个或更多
- 但是一般是2个向量组--组成XOY平面，而3个向量组组成XOYOZ空间
- V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
- 也就是某向量组{v1,v2...vn} 进行任意线性组合，其结果仍然在向量空间内。
3.3.1 线性组合的具体方法
线性组合的方法包含如下这些：
- 加法
- 标量乘法
3.4 线性变换
线性变换包含，行的线性变换和列的线性变换
行的线性变换
- 行之间，交换
- 某行乘以倍数
- 某行乘倍数+到其他行
列的线性变换
- 列之间，交换
- 某列乘以倍数
- 某列乘倍数+到其他列
3.5 线性变换（线性映射）的意义？
线性变换，指的是线性空间上，满足
T(α+β)=T(α)+T(β)
T(kα)=kT(α)
那这和直线有什么关系？
- 见线性相关的定义，这个和成正反比例关系很大，和直线的关系也有！
- 标量乘法：数乘运算，可以看作直线上做伸缩+方向变换
- 加法运算：可以用三角形法则，首位相接的形式可以来解释，2个分段向量可以等价于1个总向量图形上生成的还是直线。
- 这种映射把空间里原来的 直线，仍然映射成 直线，而不会“扭曲”成曲线；
- 同时保持原点不动(原点动的就叫“仿射变换”了…)