多层感知机（MLP）算法原理和代码实现

多层感知机入门

神经网络在最近几年，是个很火的名词了。常听到的卷积神经网络(CNN)或者循环神经网络(RNN），都可以看做是神经网络在特定场景下的具体应用方式。

本文我们尝试从神经网络的基础：多层感知机（Multilayer perceptron, MLP）入手，以此了解其解决预测问题的基本算法原理。

要入门MLP，个人认为比较简单的方式是将其理解为一种广义的线性模型。

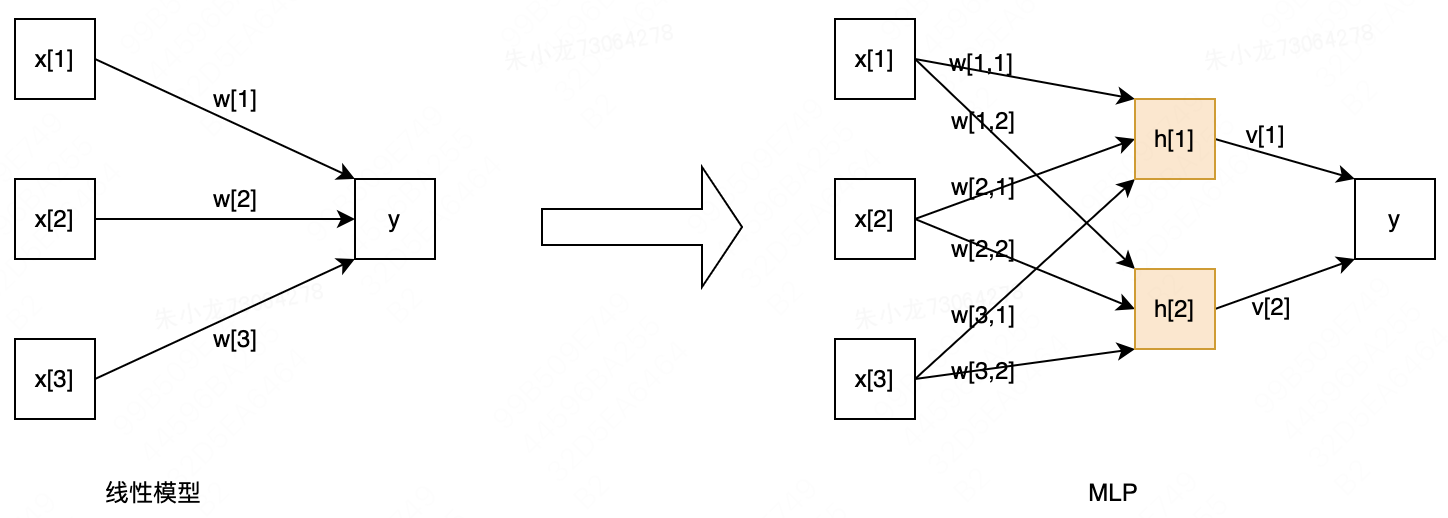
看上图，对于线性模型（左上图）
$$y=w[1]\ast x[1]+w[2]\ast x[2]+w[3]\ast x[3]+b$$
对于MLP（右上图），$x$和$y$之间增加了一组黄色的$h$模块，叫隐藏层。

$y$、$h$和$x$的关系为
$$h[1]=f(w[1,1]x[1]+w[2,1]x[2]+w[3,1]x[3]+b[0])$$
$$h[2]=f(w[1,2]x[1]+w[2,2]x[2]+w[3,2]x[3]+b[1])$$
$$y=v[1]h[1]+v[2]h[2]+s$$
其中，$f(\cdot )$是某个非线性函数，叫激活函数。

从数学上来看，如果$f(\cdot )$是线性的，那么增加了隐藏层的MLP本质上还是一个线性模型。为了让MLP的学习能力更强大，$f(\cdot )$需要使用非线性函数，目前应用比较多的有校正非线性（relu）、正切双曲线(tanh)或sigmoid函数。

三个函数的表达式分别为
$$\text{relu}:y=max(0,x)$$
$$\text{tanh}:y=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
$$\text{sigmoid}:y=\frac{1}{1+e^{-x}}$$
以下是它们各自对应的图形

此处最直接的一个疑问是，为什么有了这些激活函数后，学习能力就能变强大了？

我们可以这样理解：任意非线性函数都可以用多个分段线性函数来表示，即分段线性函数可以拟合任意非线性函数。而relu显然可以拟合分段线性函数，所以理论上便可以拟合任意非线性函数；从图上看，tanh和sigmoid可以认为是软化后的relu，所以对拟合效果影响不大，而且这两个函数计算梯度会更方便。

MLP的设计其实还有一种理解，就是看成是基于生物神经元的抽象模型，这也是神经网络模型的最初由来。神经元的结构如下，MLP和它的形状确实很像了。

算法优化原理

在上一节中，隐藏层只有1层，该层中也只有2个隐藏单元，变量的总个数为11个。但实际上，隐藏层的数量和每个隐藏层中的隐藏单元数量都可以为更多个，此时变量的个数就更多了。那么，该如何找到这些变量的最优值呢？

回到MLP设计的初衷，我们是要让MLP针对样本的预测误差最小。针对任意一个样本，误差可以定义为
$$Loss=(y-\hat{y}{)}^2$$
还是以之前的实例为例，上式变为
$$Loss=[y-(v_{1}f(w_{11}{x}_1+w_{21}{x}_2+w_{31}{x}_3+b_0)+v_{2}f(w_{12}{x}_1+w_{22}{x}_2+w_{32}{x}_3+b_1)+s){]}^2$$
如果训练集中共有$N$个样本，那么需要将每个样本的误差加和，并使其最小化
$$min\sum _{i=1}^{N}Los{s}_i$$
上式中，待优化变量为$v,w,b$和$s$，而且为无约束问题，因此可以通过梯度类算法求解。

经典的梯度类算法，可以参考梯度类算法原理：最速下降法、牛顿法和拟牛顿法。不过由于MLP中的优化变量数量通常非常大，优化过程较为耗时，所以像牛顿法这类需要计算海森矩阵的算法自然是不合适的；即使是拟牛顿法这种已经使用其他方案替代海森矩阵的算法也逐渐被大家舍弃；最终，在提升训练效率的驱使下，人们普遍选择了最速下降法这类只需要一阶梯度的算法作为基本算法。

既然需要使用一阶梯度的信息，那么该如何计算梯度呢？在计算之前，我们要先理清楚的是，这里的梯度，指的是损失函数Loss针对优化变量为$v,w,b$和$s$的梯度。

我们以Loss针对$w$的梯度为例，说明一下求解过程。还是使用之前的MLP实例，同时把表达式写成矩阵形式
$$h=f(w^{T}x+b)\Rightarrow \frac{\partial h}{\partial w^T}=f^{\prime }\cdot x$$
$$\hat{y}=v^{T}h+s\Rightarrow \frac{\partial \hat{y}}{\partial h}=v^T$$
$$Loss=(y-\hat{y}{)}^2\Rightarrow \frac{\partial Loss}{\partial \hat{y}}=y-\hat{y}$$
根据求导的链式法则
$$\frac{\partial Loss}{\partial w^T}=\frac{\partial Loss}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial h}\cdot \frac{\partial h}{\partial w^T}=(y-\hat{y})\cdot v^T\cdot f^{\prime }\cdot x$$
这就是我们常说的：误差反向传播，此处可以理解为梯度计算的过程是从后向前逐步推导过来的。

以上实例给的是，针对一个样本的梯度求解过程。为了得到准确的梯度值，就需要针对每个样本都走一遍如上的过程。如果我们的训练样本数量比较大，就会导致梯度计算的过程非常慢。

如果换个思路来处理，我们每次只计算其中一个样本的梯度值，然后将该值作为最终的梯度值，那么结果就是梯度的计算过程快但值不那么准确。

所以当下流行的折中方案是，每次挑选一部分样本（batch）出来，计算出梯度值作为整体的梯度值。通过batch数量的调整，便可以兼顾计算的效率和值的准确性。

有了梯度后，我们回顾一下梯度类算法的基本迭代公式：
$${\theta }_{k+1}={\theta }_k-{\eta }_k\cdot d_k$$
其中，$\theta$表示优化变量，${\eta }_k$和$d_k$分别为第$k$次的迭代步长(MLP中更多称之为“学习率”)和迭代方向。

在最速下降法中
$$d_k=\frac{\partial Loss}{\partial \theta }=\nabla (\theta )$$

$d_k$的计算过程刚刚已经描述了。如果算法逻辑到此为止，我们一般会称之为随机梯度下降法（Stochastic gradient descent，SGD）。

但是，人们一般很难满足于这种比较基础的算法，所以在此之上，相继出现了很多改进算法。从迭代公式可以看出，改进点主要包含3类：第一类是针对迭代方向，如Momentum；第二类是针对学习率，如Adagrad；第三类是同时改进迭代方向和学习率，如Adam。具体改进的策略可以参考学术文献：An overview of gradient descent optimization algorithms。

sklearn代码实现

sklearn中已经集成了MLP的工具包，下例中使用分类功能：MLPClassifier。该函数参数的含义可以参考MLPClassifier参数详解。数据集我们使用two_moons，该数据集的详细介绍可以参考之前的文章：决策树入门、sklearn实现、原理解读和算法分析。

import mglearn.plots
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier

from data.two_moons import two_moons
import matplotlib.pyplot as plt


def train_two_moons():
    # 导入两个月亮数据集
    features, labels = two_moons()
    
    # 将数据集分为训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(features, labels, stratify=labels, random_state=42)
    # 设置 MLP 分类器属性：激活函数为tanh，2个隐藏层，每层均包含10个隐藏单元，最大迭代次数为1000
    mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=[10, 10], max_iter=1000)

    # 使用训练集对 MLP 分类器进行训练
    mlp.fit(X_train, y_train)
    # 打印模型在训练集上的准确率
    print('Accuracy on train set: {:.2f}'.format(mlp.score(X_train, y_train)))
    # 打印模型在测试集上的准确率
    print('Accuracy on test set: {:.2f}'.format(mlp.score(X_test, y_test)))
    
    # 绘制 2D 分类边界
    mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
    # 绘制训练集的散点图
    mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
    # 设置 x 轴标签
    plt.xlabel("Feature 0")
    # 设置 y 轴标签
    plt.ylabel("Feature 1")
    

if __name__ == '__main__':

    train_two_moons()

运行以上代码后，首先可以得到MLP的性能指标：

Accuracy on train set: 1.00
Accuracy on test set: 0.84

然后还可以得到该模型的决策边界。显然，该决策边界是非线性的，但是看起来还算平滑。

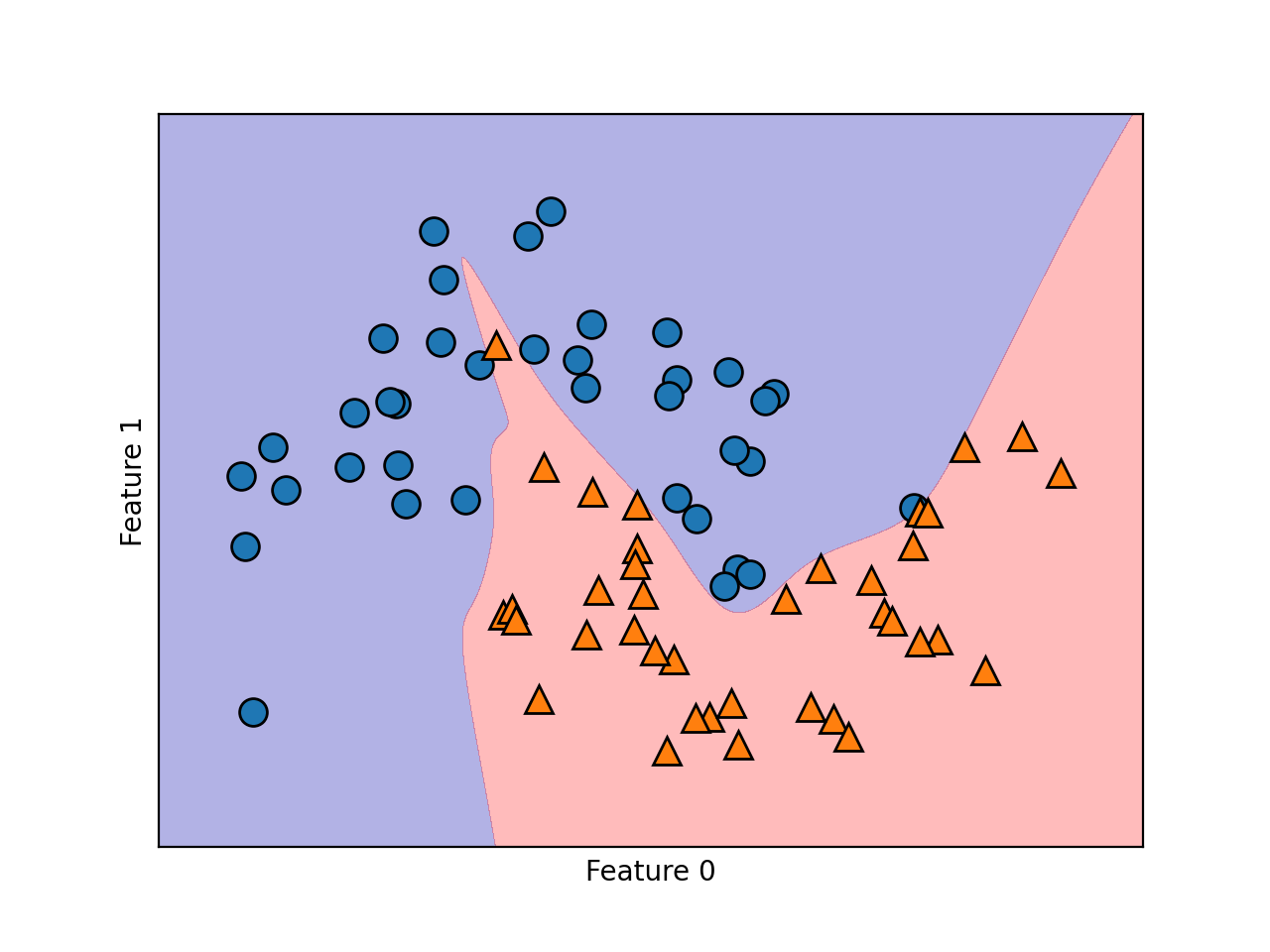
核心优缺点分析

MLP的主要优点是，可以通过调整隐藏层的层数和每个隐藏层内的隐藏单元数，构建出复杂的模型，从而学习到数据中包含的各类信息。如果给予足够的计算时间和数据，并且仔细调节参数，MLP通常可以打败其他机器学习算法（无论是分类任务还是回归任务）。

其主要缺点有两个：第一个是复杂模型往往需要花费较长的时间去训练模型中的参数，第二节中SGD->Momentum、Adagrad->Adam的算法进化，可以理解为人们尝试通过算法改进的方式，降低模型训练的总时间；第二个是可解释差，即我们无法解释清楚模型给出某个预测结果的原因，所以这个模型很多时候也被称之为黑箱模型。