本博客仅为作者记录笔记之用,不免有很多细节不对之处。
还望各位看官能够见谅,欢迎批评指正。
从线性回归到逻辑回归[1]
逻辑回归(Logistic Regression)不是回归问题,而是一个分类问题。这里先从二元分类开始讨论。
笔记1我们说到了线性回归,然后线性回归只能预测连续的值。然而对于分类问题,我们需要输出0或1。
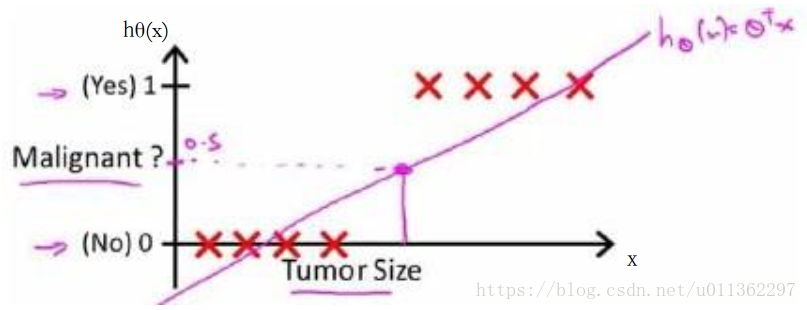
如果我们继续用线性回归来解决分类问题,如下图所示我们将获得一条粉红色直线。我们可以设定阈值0.5,对于输入x,当hθ(x) ≥ 0.5时,我们认为x是1类,当hθ(x) < 0.5时,我们认为x是0类。这好像也解决了我们的分类问题,然而事实并非如此。
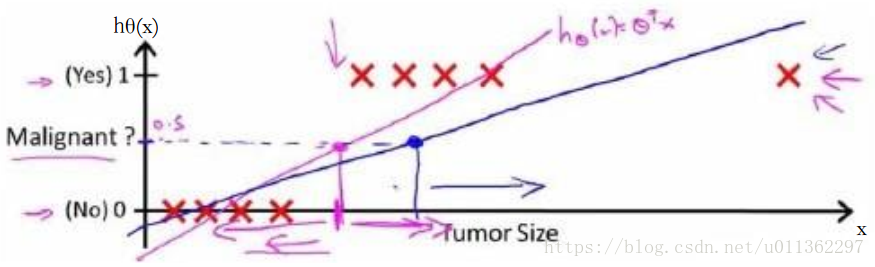
假设我们又观测到一个很大的1类,我们将其加入到我们的训练集中来,我们将获得一条如下图所示蓝色的直线。这时候再使用0.5作为阈值便不合适了。可以看出,线性回归模型,因其预测的值可以超越[0,1]的范围,并不适合解决这样的分类问题。
判定边界
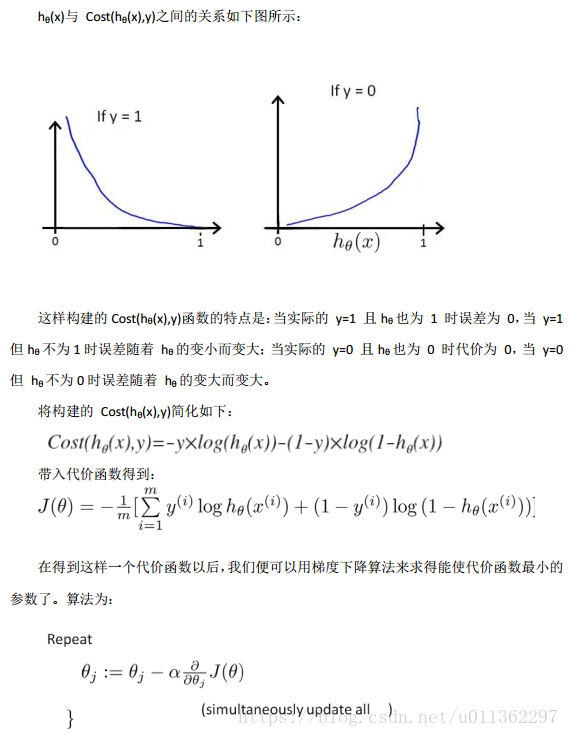
代价函数
这里为什么是非凸函数?
为什么这里的代价函数可以这样定义?
求导后得到:
怎么求导得到的?
代码示例[2]
批量梯度上升算法
{
每个回归系数初始化为1
重复R次:
计算整个数据集的梯度
w := w + alpha * gradient更新回归系数向量
返回回归系数
}
梯度上升拟合直线:w0*x0 + w1*x1 + w2*x2 = 0,这里x0 = 1
#!/usr/bin/python
# -*- coding: UTF-8 -*-
'''
Created on Oct 27, 2010
Logistic Regression Working Module
@author: Peter
'''
from numpy import *
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
weights_arr = []
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n, 1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
# 梯度上升法
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose() * error # matrix mult
# 梯度下降法
#error = (h - labelMat) # vector subtraction
#weights = weights - alpha * dataMatrix.transpose() * error # matrix mult
weights_arr.append(weights.tolist())
return weights, weights_arr
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
plt_util.py
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
def plot31(x, y0, y1, y2):
plt.figure(1)
plt.title("show example")
plt.subplot(311)
plt.plot(x, y0, marker='.', mec='r')
plt.ylabel("w0")
plt.subplot(312)
plt.plot(x, y1, marker='.', mec='r')
plt.ylabel("w1")
plt.subplot(313)
plt.plot(x, y2, marker='.', mec='r')
plt.ylabel("w2")
plt.xlabel(u"iterations")
plt.show()
main.py
import numpy as np import logRegres import plt_util as plutil # 批量梯度上升 dataArr, labelMat = logRegres.loadDataSet() weights, weights_arr = logRegres.gradAscent(dataArr, labelMat) print(weights) logRegres.plotBestFit(weights.getA()) weights_mat = np.array(weights_arr) y0 = weights_mat[0::1, 0] y1 = weights_mat[0::1, 1] y2 = weights_mat[0::1, 2] x = range(0, len(y0)) plutil.plot31(x, y0, y1, y2)
拟合出的最佳分类直线如下图所示
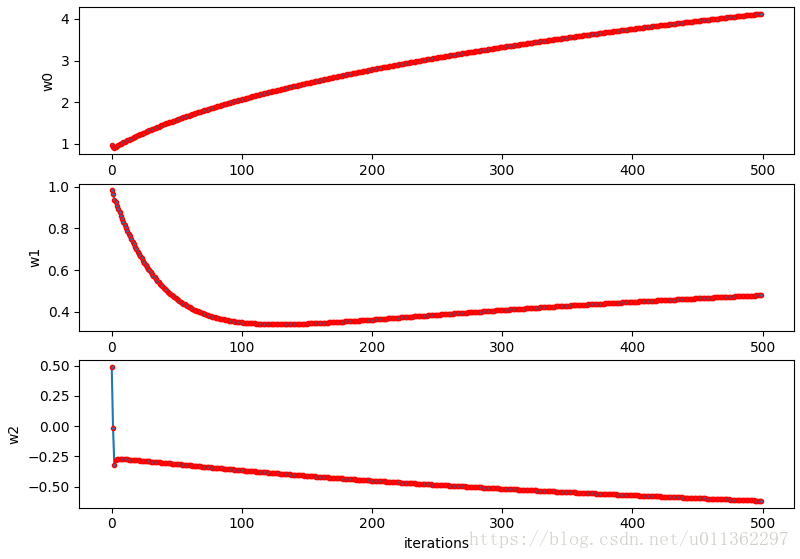
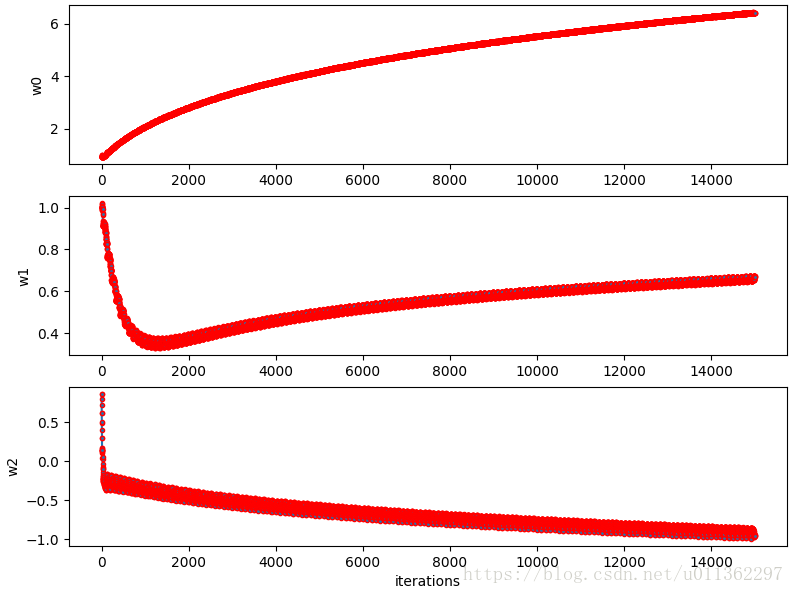
训练参数w和迭代次数的关系如下图:
随机梯度上升算法
{
所有回归系数初始化为1
重复R次: # (文献[2]将这里的迭代R次算作是改进的随机梯度上升法)
对数据集中的每个样本:
计算该样本的梯度
w := w + alpha * gradient更新回归系数值
返回回归系数
}
更新到logRegres.py
def stocGradAscent0(dataMatrix, classLabels, numIter=150):
weights_arr = []
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for j in range(numIter):
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
weights_arr.append(weights.tolist())
return weights, weights_arr
main.py
from numpy import * import logRegres dataArr, labelMat = logRegres.loadDataSet() weights = logRegres.stocGradAscent0(array(dataArr), labelMat) print(weights) logRegres.plotBestFit(weights)
拟合出的最佳分类直线如下图所示:
训练参数w和迭代次数的关系如下图:
和采用批量梯度上升法相比,对于使参数w达到某一数值,随机梯度上升会更快。
若记录每一次参数更新后的w值,则得图如下:
观察上图可知,在大的波动停止后,还有一些小的周期性波动,这是由于存在一些不能正确分类的样本点(数据并非线性可分),在每次迭代时会引发系数的剧烈改变。我们期望算法能避免来回波动,从而收敛到某个值。另外,收敛速度也需要加快。
改进的随机梯度上升法
针对上述问题,对梯度上升法作如下改进。
1. 学习率alpha在每次迭代时都会调整。这会缓解上图中的数据波动或者高频波动。
2. 随机选取样本来更新回归系数。这将减少周期性的波动。
更新到logRegres.py
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
weights_arr = []
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
weights_arr.append(weights.tolist())
return weights, weights_arr
main.py
import numpy as np import logRegres import plt_util as plutil # 随机梯度上升 dataArr, labelMat = logRegres.loadDataSet() weights, weights_arr = logRegres.stocGradAscent1(np.array(dataArr), labelMat) logRegres.plotBestFit(weights) print(weights) weights_mat = np.array(weights_arr) y0 = weights_mat[0::1, 0] y1 = weights_mat[0::1, 1] y2 = weights_mat[0::1, 2] x = range(0, len(y0)) plutil.plot31(x, y0, y1, y2)拟合出的最佳分类直线如下:
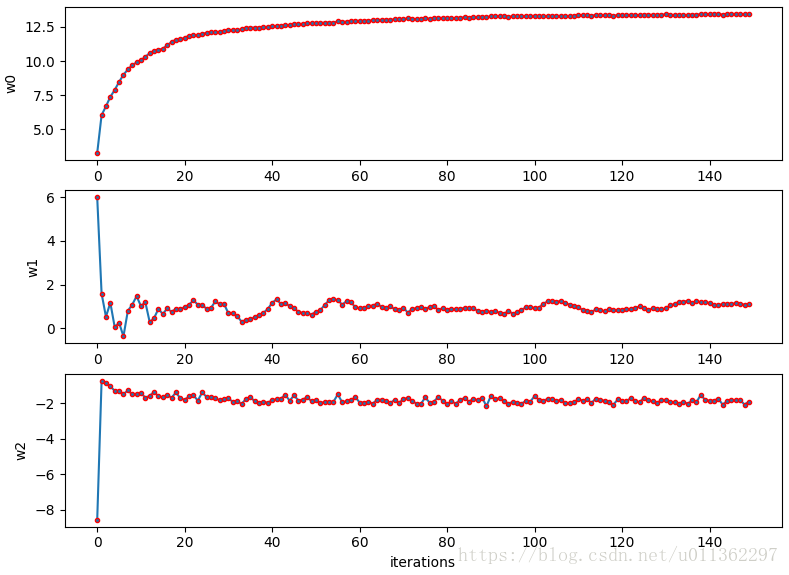
训练参数w和迭代次数的关系如下图:
若记录每一次参数更新后的w值,则得图如下:
参考文献
[1] 黄海广. MIT 机器学习教程
[2] Peter. 机器学习实战