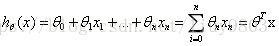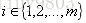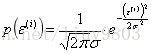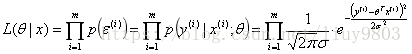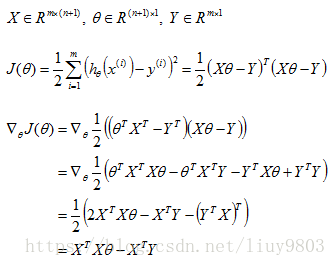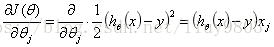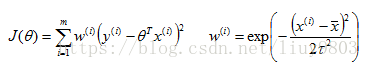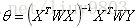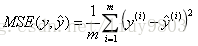回归算法是一种有监督学习算法,用来建立自变量X和观测变量Y之间的映射关系,如果观测变量是离散的,则称其为分类Classification;如果观测变量是连续的,则称其为回归Regression。
回归算法的目的是寻找假设函数hypothesis来最好的拟合给定的数据集。常用的回归算法有:线性回归(Linear Regression)、逻辑回归(Logistic Regression)、多项式回归(Polynomial Regression)、岭回归(Ridge Regression)、LASSO回归(Least Absolute Shrinkage and Selection Operator)、弹性网络(Elastic Net estimators)、逐步回归(Stepwise Regression)等。
线性回归模型试图学得一个线性模型以尽可能准确地预测实值X的输出标记Y。在这个模型中,因变量Y是连续的,自变量X可以是连续或离散的。
在回归分析中,如果只包括一个自变量和一个因变量,且二者关系可用一条直线近似表示,称为一元线性回归分析;如果回归分析中包括两个或两个以上的自变量,且因变量和自变量是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线,对于三维空间线性是一个平面,对于多维空间线性是一个超平面。
1、目标函数:
根据数据特征寻找合适的假设函数hθ(x),构造适合的损失函数J(θ)。求极大似然估计的最大值,或由极大似然可推导出最小二乘函数,求它的最小值。
构造假设函数:
其中 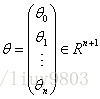
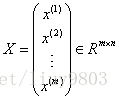
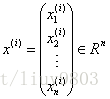
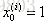
m:输入数据的条数;n:每条数据的特征个数
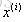
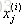
向量化Vectorization 相比传统的for循环求解更简洁、速度也更快。
(1)MLE
在实际问题中,很多随机现象可看做是由众多因素独立影响的综合反映,往往服从正态分布(中心极限定理),因此可知线性回归的误差是独立同分布的,服从均值为0,方差为某定值σ2的Gaussian分布。
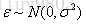
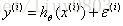
写出误差概率/概率密度的似然函数并求其对数,该似然函数与它的对数的单调性、取到极值点时的x值相同:
由极大似然估计MLE原理可知,为了使l(θ)取得最大值,需要让减号这部分 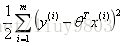
(2)OLS
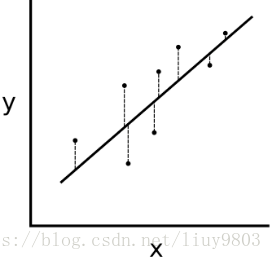
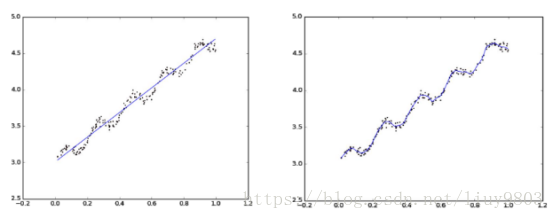
通过最小化误差的平方和寻找数据的最佳函数匹配,即求所有观察值的残差平方和的最小值(下图虚线段平方和的最小值)。最小二乘法可以将误差方程转化为有确定解的代数方程组——正规方程/法方程(Normal Equation),是一种区别于迭代方法的直接解法。
最小二乘法只能解决线性最小二乘问题,而逻辑回归的损失函数就不是最小二乘问题(不服从正态分布)。
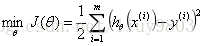
MLE和OLS的区别:
分别是两种不同原理的参数估计方法,最大似然估计是以最大化抽取值的似然概率作为目标,最小二乘法是以最小化估计值与实际值之差的平方和作为目标。
最大似然函数需要已知概率分布或概率密度函数,一般假设其服从正态分布,这样得到的最大似然函数与最小二乘法的结果相同。即由Gaussian分布和MLE可解释最小二乘法函数式的形式(为什么OLS用平方而不是绝对值、四次方等)。
2、求解算法:
梯度下降法BGD/SGD/MBGD迭代求θ;解方程对数极大似然偏导等于0直接求θ,即最小二乘法解析解直接求θ值。
(1)直接求解——最小二乘法解析解
令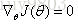

XTX不可逆(singular/ degenerate)的解决方法:
① 使用np.linalg.pinv(mat1, mat2)函数求伪逆;
② 扩充数据集——增加m值;
③ X降维,删除不重要的特征、消除特征之间的线性依赖;
④ 正则化,增加额外的数据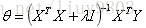
(2)迭代求解——梯度下降法Gradient Descent
要求某函数的极小值,应沿着该函数梯度下降的方向迭代求解。具体到线性回归模型,要求的极小值,需要:
i. 初始化θ(随机初始化θ,可以初始为0);
ii. 沿着J(θ)负梯度方向迭代,更新后的θ使J(θ)更小;
iii. 不断迭代直到达到某个停止条件为止,如迭代次数达到某个指定的值,或算法达到某个可以允许的误差范围。
梯度算法的迭代公式为:
repeat until convergence {
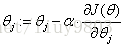
}
α:学习率/步长
其中线性模型的偏导项:
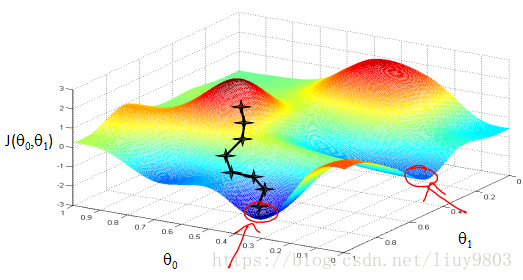
由于梯度下降算法以负梯度方向作为变量的变化方向,所以有可能导致最终求解的值是局部最优解。Andrew Ng PPT
所以在使用梯度下降算法的时候,需要进行一些调优策略:
①学习率的选择
学习率过大,表示每次迭代更新的时候变化比较大,J(θ)有可能不会收敛;学习率过小,表示每次迭代更新的变化比较小,就会导致迭代的速度过慢,很长时间都不能收敛。
学习率的选择技巧:(交叉验证)
尝试一系列α值,如0.001,0.01,0.1,1,分别画出J(θ)与迭代次数的曲线,找到使J(θ)快速下降的α值,Andrew Ng的建议是每次乘以3,即尝试0.001,0.003,0.01,0.03,0.1,0.3,1等值,直到找到一个太大的值,选择最大的合理值或略小一些的α值。
②算法初始参数值的选择
初始值不同,最终获得的最小值也有可能不同,因为梯度下降算法求解的是局部最优解,所以一般情况下,选择多次不同的初始值运行算法,最终选择损失函数最小情况下的结果值作为模型最优解。
③特征标准化
由于样本不同特征的取值范围不同,可能导致各个不同参数上的迭代速度不同,为了减少特征取值范围不同导致的影响,可以将特征进行标准化操作。
a. 批量梯度下降法BGD(Batch GD):
每次迭代使用所有m个样本。优点是每次迭代都包括了全部的样本,可以求得全局最优解,且易于并行实现;缺点是在数据量大的计算量很大。
repeat {
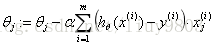
}
b. 随机梯度下降法SGD(Stochastic GD):
每次迭代使用一个样本,由于有噪音的存在,SGD的结果并不是完全收敛的,而是在波动中趋近于局部最优解,属于兼顾计算成本的折中方案。SGD适合样本量大的情况以及在线机器学习Online ML。优点是计算速度快,有时可能跳出某些小的局部最优解;缺点是准确度比BGD有所下降,且不易于并行实现。
Randomly shuffle data set;
repeat {
for i = 1 to m {
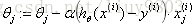
}
}
c. 小批量梯度下降法MBGD(Mini-batch GD):
若既要保证算法的训练过程比较快,又需要保证最终参数训练的准确率,可以使用MBGD算法。MBGD用b个样本(b=10,或2~100)的平均梯度作为更新方向。
Say b=10, m=1000
repeat {
for i = 1,11,21,...,991 {
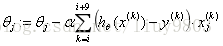
}
}
当样本量为m时,每次迭代BGD算法对于θ值更新一次,SGD对θ值更新m次,MBGD算法对θ值更新m/b次,且有时候因为MBGD可以Vectorization,可以使用高度优化的数值代数库,在b个样本上并行梯度运算,可能比SGD的计算速度还要快一些。
(3)直接求解——局部加权回归(Local weighted linear regression)
由于标准线性回归对下图的拟合效果不好,出现欠拟合情况,可以通过添加x2或sinx等特征或者用局部加权线性回归解决这个问题。
局部加权回归算法是一种非参数学习法,可看做是正规方程的一种改进,以降低估计时的均方误差。
Ø 非参数学习算法(non-parametric learning algorithm)
对所要学习的问题知之甚少,不会对目标函数的形式做过多的假设,训练开销大,泛化能力好。常见的算法有kNN、LWLR等。
Ø 参数学习算法(parametric learning algorithm)
对所要学习的问题具备一定的先验知识,可以假定目标函数的具体形式,通过训练数据集估计少量未知参数,泛化能力弱。常见的算法有LR、LDA、Naive Bayes等。
局部加权回归的损失函数、权重设置
权重w根据要预测的点与数据集中的点的距离成反相关,即当某点离要预测的点越远,其权重就越小,反之则越大。
其中,τ为波长参数bandwidth,控制权重随距离下降的速率(权重w曲线的宽窄,类似标准差)。τ值越大,远距离样本的权值下降就越快。
由最小二乘法解出θ值:
局部加权回归在每一次预测新样本的时候都会重新确定参数,从而达到更好的预测效果。当数据规模比较大的时候计算量很大,并且局部加权回归也不一定就能避免欠拟合。
3、模型评估:
(1)均方误差 MSE/RMSE(Mean Squared Error)
MSE指的是参数估计值与实际值之差的平方的期望值,这个值越小说明预测模型具有越好的精确度。RMSE是MSE的算术平方根。
使用方法:from sklearn.metrics import mean_squared_error
(2)R2值(R-Squared/Coefficient of determination)
拟合优度/决定系数R2值指回归直线对观测值的拟合程度,即将预测值与只使用均值的情况相比,,值越接近于1说明回归直线对观测值的拟合程度越好。
线性回归模型一般用R-Squared评价模型的表现。
使用方法:from sklearn.metrics import r2_score
训练集与测试集的划分
借用课件PPT
1、留出法(hold-out):
随机将初始数据集一部分划分为训练集,剩余部分作为测试集,划分时应尽量保证数据分布的一致性,一般测试集的数量少于原样本数量的三分之一左右。
2、交叉验证法(k-fold cross validation):
将初始数据集随机划分为k个互斥子集,用k-1个子集作为训练集,剩下一个作为测试集,轮流将每一个子集作为测试集,一共进行k次建模,最终得到测试结果的均值(score的平均得分)。k值一般为5、10。
将数据集随机划分为k个互斥子集,一共进行p次这样的操作,最后对p个k-fold cv进行取平均,称为p次k折交叉验证。
交叉验证法的目的:校准当前模型的准确率score(注意和GridCV的区别)
3、留一法LOOCV(Leave-one-out cross validation):
若数据集一共有m个样本,随机令一条数据作为测试数据,其他作为训练数据,这种划分方法是交叉验证法的特殊情况。这种划分方法的优势是,每个模型都能很好的反应原始数据集的特性;缺点是计算量在数据量大的时候会非常大,还不算调超参的计算量。
4、自助法(Bootstrapping):
对数据集D中的m个数据进行有放回的随机取样,重复m次,产生一个新的数据集D’,将未被取到的数据集作为测试集。数据从未被取到的的几率约为36.8%。
注意:模型的好坏和训练集、测试集的划分无关,而是和参数、算法选择等有关,因此不必过于纠结划分方式的选择。