【人工智能】— 维度灾难、降维、主成分分析PCA、获取旧数据、非线性主成分分析

高维数据与维度灾难

大多数机器学习和数据挖掘技术对于高维数据可能不太有效。这是由于维度灾难（Curse of Dimensionality）导致的。

随着维度的增加，查询的准确性和效率会迅速下降。因此，在高维数据中，许多机器学习和数据挖掘技术可能无法处理。

然而，高维数据的内在维度可能很小。例如，在某种类型的疾病中负责的基因数量可能很少。因此，对于高维数据，需要使用专门针对高维数据的技术，如降维和特征选择，以提高机器学习和数据挖掘的效率和准确性。

维度灾难

在高维数据中，维度灾难（Curse of Dimensionality）会导致以下问题：

• 随着维度的增加，数据在所占用的空间中变得越来越稀疏。
• 密度和点之间的距离的定义对于聚类和异常检测变得越来越无意义。
• 如果 $N_1=100$ 表示单个输入问题的密集样本，则在维度为 $10$ 的情况下，需要样本量为 $N_{10}=100^{10}$ 才能获得相同的采样密度。
• 半径为 $r$、维度为 $d$ 的超球体与边长为 $2r$、维度为 $d$ 的超立方体之间的比例在 $d$ 趋近于无穷时收敛于 $0$，即几乎所有的高维空间都“远离”中心。
  

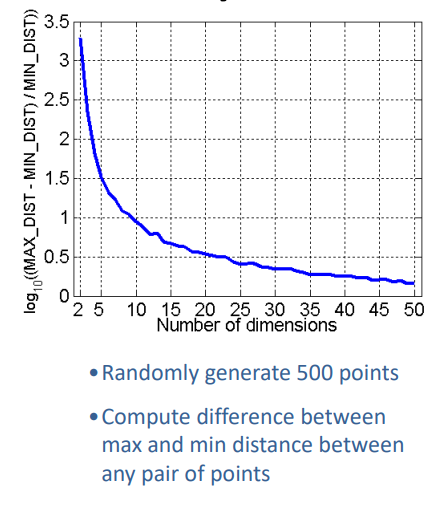
因此，对于高维数据，需要特别注意选择适当的特征和降维技术，以便提高数据的密度和距离的意义，同时减少维度灾难的影响。

降维

降维（Dimensionality Reduction）是指将原始高维数据映射到低维空间的过程。

在不同的问题设置下，降维的标准可能会有所不同：

• 无监督学习：最小化信息损失；
• 监督学习：最大化类别差异。

给定由 $d$ 个变量组成的数据点集合，可以计算将数据映射到低维空间的线性变换（投影）。设 $f(x_1,x_2,\dots ,x_n)$ 是在 $R^d$ 上的原始数据点， $P$ 是一个 $R^{d\times m}$ 的矩阵，表示投影。则，变换后的数据点 $y$ 由 $y=P^{T}f(x_1,x_2,\dots ,x_n)$ 得到，其中 $m\ll d$。

因此，可以通过找到最优投影矩阵 $P$，在保留重要特征和最小化信息损失的同时降低数据维度，从而实现降维的目的。常用的降维技术包括主成分分析（PCA）和线性判别分析（LDA）等。

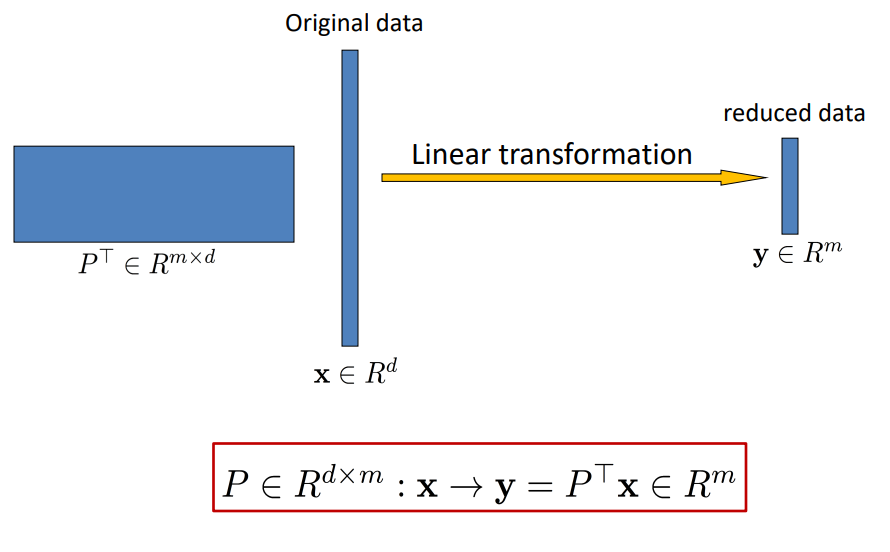
为什么需要降维？

降维（Dimensionality Reduction）有以下应用：

• 可视化：将高维数据投影到二维或三维平面上，以便可视化和理解数据的结构和特征。
• 数据压缩：降维可以减少数据的维度，从而提高数据的存储和检索效率。
• 噪声去除：降维可以去除冗余和不相关的特征，从而对查询准确性产生积极影响。

因此，降维是在处理高维数据时非常重要的技术，可以帮助我们更好地理解和利用数据。

PRINCIPLE COMPONENT ANALYSIS

主成分分析（Principal Component Analysis，PCA）是一种常用的无监督学习算法，用于降低数据的维度并发现数据中的主要成分。

维度降低（Dimensionality reduction）是指通过减少数据的特征维度，将高维数据映射到低维空间中。维度降低的目的有以下几个方面：

1. 数据压缩：高维数据可能包含冗余信息，通过降维可以减少存储空间和计算开销。
2. 特征选择：降维可以帮助选择最相关的特征，去除噪音或不重要的特征，提高模型的效果和泛化能力。
3. 可视化：降维可以将高维数据可视化在二维或三维空间中，更直观地理解数据之间的关系。

主成分分析（PCA）是一种经典的降维技术。它通过线性变换将原始数据映射到一组新的正交特征上，这些特征被称为主成分。PCA的目标是找到能够最大化数据方差的投影方向，从而保留尽可能多的数据信息。通过PCA，可以对数据进行降维，将其表示为较少数量的主成分，其中每个主成分都是原始特征的线性组合。

非线性PCA使用核函数（Kernels）扩展了传统的PCA方法，使其能够处理非线性数据。通过应用核函数，可以将原始数据映射到高维特征空间，然后在该空间中进行线性PCA。这样可以处理非线性关系，发现更复杂的数据结构和模式。

主成分的几何图像

在主成分分析中，主成分可以通过几何图像来理解。对于在 $d$ 维空间中的 $n$ 个数据点，主成分分析可以将数据投影到一维空间中。

具体地，可以选择一条直线，使得数据点在该直线上分布得很好。这条直线被称为主成分。主成分是在保留数据大部分信息的前提 下，将数据投影到一维空间中的最佳方式。

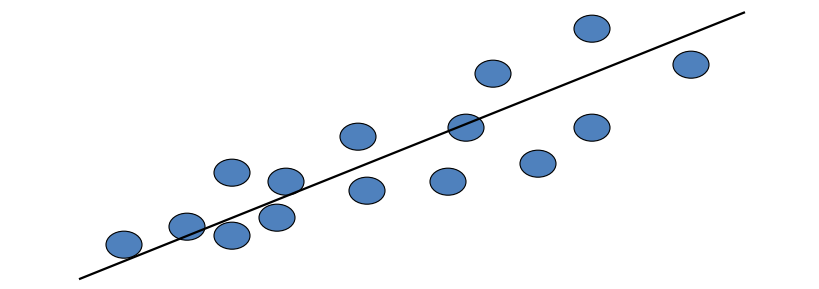
主成分的选择可以通过计算数据的协方差矩阵和对该矩阵进行特征值分解来实现。每个特征向量都代表了在数据中的一个主要方向，并且与该方向上的方差成比例。因此，可以选择特征值最大的几个特征向量来作为主成分，并将数据投影到这些方向上。

最小化到直线距离的平方和

在主成分分析中，为了找到最佳的主成分，需要最小化数据点到该主成分投影的距离的平方和。这是因为，最小化这个距离的平方和可以最大化数据点在主成分上的投影的平方和。

具体地，可以将每个数据点表示为向量 $\mathbf{x}$，然后将其投影到主成分上得到向量 $\mathbf{p}$。这个投影可以通过将向量 $\mathbf{x}$ 投影到主成分的单位向量 $\mathbf{u}$ 上来实现，即 $\mathbf{p}=\mathbf{x}\cdot \mathbf{uu}$。

然后，最小化每个数据点到主成分的距离的平方和，可以表示为以下式子：

$$\sum _{i=1}^n\Vert {\mathbf{x}}_i-{\mathbf{p}}_i{\Vert }^2$$

其中，$\Vert \cdot \Vert$ 表示向量的范数。将向量 ${\mathbf{p}}_i$ 替换为 ${\mathbf{x}}_i\cdot \mathbf{uu}$，可以得到以下式子：

$$\sum _{i=1}^n\Vert {\mathbf{x}}_i-({\mathbf{x}}_i\cdot \mathbf{u})\mathbf{u}{\Vert }^2$$

为了最小化这个式子，需要最大化每个数据点在主成分上的投影的平方和。这是由于，根据勾股定理，数据点到主成分的距离的平方和等于每个数据点在主成分上的投影与该数据点之间的距离的平方和。因此，最小化数据点到主成分的距离的平方和等价于最大化每个数据点在主成分上的投影的平方和。

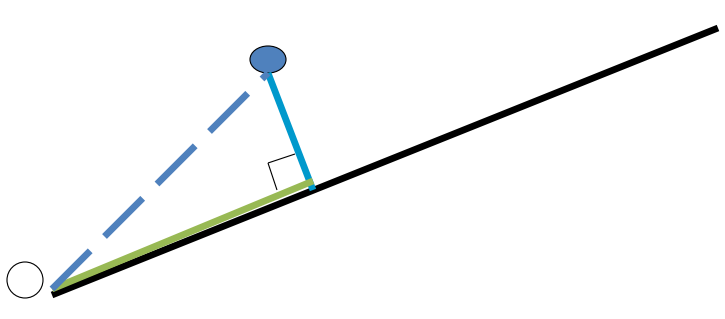
综上所述，为了找到最佳的主成分，需要最大化每个数据点在主成分上的投影的平方和，即最小化数据点到主成分的距离的平方和。

举例

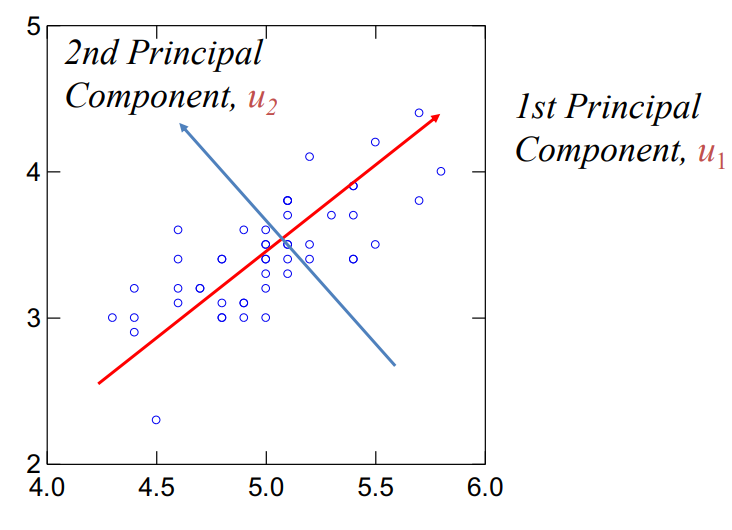
具体来说，第一个主成分是对原始数据的最小距离拟合，以得到一条直线，使得数据点在该直线上分布得很好。该直线是在保留了数据大部分信息的情况下，将数据投影到一维空间中的最佳方式。

第二个主成分是在与第一个主成分正交的平面上进行的最小距离拟合。该平面是由第一个主成分所定义的直线所张成的平面的垂直平面。通过这个过程，可以找到另一条直线，使得数据点在该直线上分布得很好，并且与第一个主成分正交。

主成分的代数推导

在主成分分析中，主成分可以通过代数推导来获得。设有一个 $d$ 维的数据集，其中包含 $n$ 个数据点，可以将其表示为一个 $d\times n$ 的矩阵 $X$。我们的目标是找到一个 $d$ 维的向量 $\mathbf{u}$，使得将数据投影到该向量上时，投影数据的方差最大。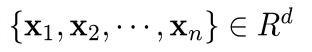

具体来说，我们首先将数据投影到一个 $d$ 维的向量 $\mathbf{u}$ 上，得到一个一维的数据集 $Y={\mathbf{u}}^{\top }X$。

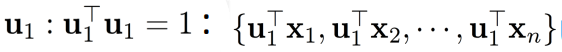
然后，我们要找到一个$u_1$最大化这个数据集的方差，即：

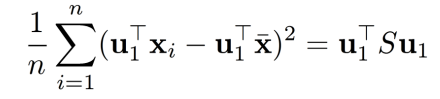
优化问题

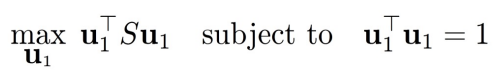
我们可以使用拉格朗日乘数法来求解主成分。具体来说，我们要求解以下问题：

$$\underset{\mathbf{u}}{\max }{\mathbf{u}}^{\top }S\mathbf{u}\text{ subject to}{\mathbf{u}}^{\top }\mathbf{u}=1$$

其中，$S$ 是数据的协方差矩阵。我们可以使用拉格朗日乘数法将约束条件加入目标函数中，得到：

$$L(\mathbf{u},\lambda )={\mathbf{u}}^{\top }S\mathbf{u}-\lambda ({\mathbf{u}}^{\top }\mathbf{u}-1)$$

其中，$\lambda$ 是拉格朗日乘数。对 $\mathbf{u}$ 和 $\lambda$ 分别求导并令其等于零，可以得到：

$$\begin{array}{rl}\frac{\partial L}{\partial \mathbf{u}}& =2S\mathbf{u}-2\lambda \mathbf{u}=0\\ & \\ \frac{\partial L}{\partial \lambda }& ={\mathbf{u}}^{\top }\mathbf{u}-1=0\end{array}$$

将第一个式子中的 $\mathbf{u}$ 提出来，可以得到：

$$S\mathbf{u}=\lambda \mathbf{u}$$

这个式子说明，投影向量 $\mathbf{u}$ 是数据集的协方差矩阵 $S$ 的特征向量，对应的特征值为 $\lambda$。因此，可以通过计算协方差矩阵 $S$ 的特征向量和特征值，来确定投影向量 $\mathbf{u}$，以及数据在该投影向量上的投影。通过类似的方式，可以确定更多的主成分。每个主成分都是在前面主成分所定义的子空间上进行的最小距离拟合，并且与前面的主成分正交。

计算主成分（Principal Components, PCs）的主要步骤

计算数据的协方差矩阵 $S$。

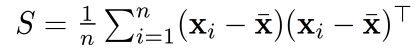
如果数据没有被中心化，则需要先将每个变量的均值减去每个观测值: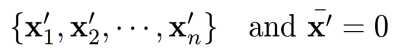，然后再计算 $S$。

找到前 $m$ 个特征向量。

通过解特征向量问题得到 $S\mathbf{u}=\lambda \mathbf{u}$ 的特征向量 $\mathbf{u}$，并按照对应的特征值 $\lambda$ 从大到小排序，选取前 $m$ 个特征向量。
形成投影矩阵 $P$。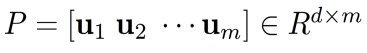

将前 $m$ 个特征向量按列组成矩阵 $P$，这个矩阵可以将数据投影到前 $m$ 个主成分所张成的子空间中。
对一个新的测试点进行投影。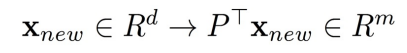

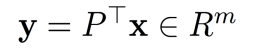获取旧数据的方法？

如果P是一个方阵，我们可以通过下式来恢复x。

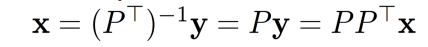
在这种情况下，P并不是满秩的，但我们仍然可以通过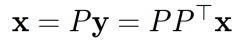来恢复x，并且会丢失一些信息。

• 目标：损失最少的信息

主成分分析的最优性性质

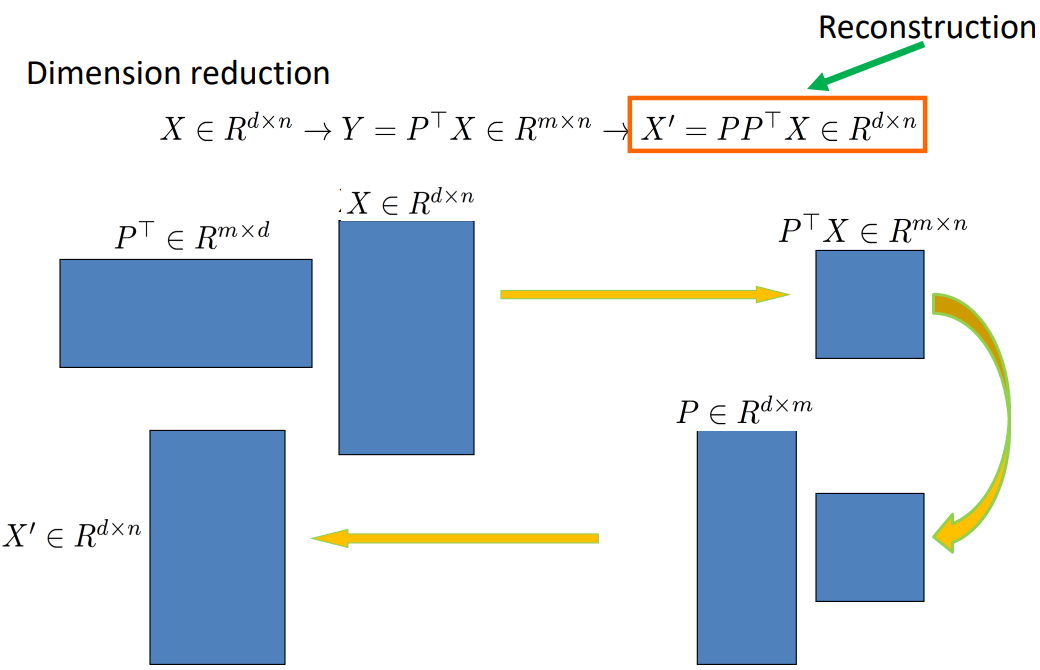
主要的理论结果

由协方差矩阵S的前m个特征向量组成的矩阵P解决了以下最小问题：

其中，P 是由协方差矩阵 S 的前 m 个特征向量组成的矩阵。

PCA投影使大小为m的所有线性投影中的重建误差最小化。

PCA图像压缩

使用核的非线性主成分分析

根据点积重写PCA

• 假设数据已经中心化

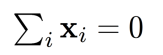
• 协方差矩阵S可以写成

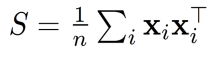
• 如果$u$是对应于非零特征值的S的特征向量

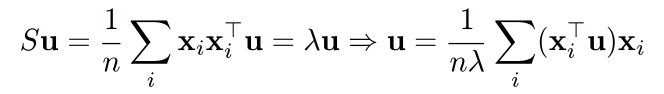
• S的特征向量位于由所有数据点跨越的空间中

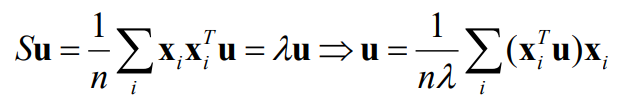
• 协方差矩阵可以写成矩阵形式：
  

评价

PCA（主成分分析）的评论：

• PCA是一种线性降维方法。

• PCA可以进行核化处理，从而可以处理非线性问题。

• 许多非线性降维方法（如Isomap、图拉普拉斯特征映射和局部线性嵌入/LLE）可以看作是使用特殊核的核PCA。

• PCA是一个非凸优化问题，但是相对容易求解。

• PCA是一种在统计学和机器学习中广泛应用的方法，它可以用于数据降维、特征提取、数据可视化等领域。PCA能够提取数据中最重要的特征，并将数据投影到低维空间中，以便更好地理解数据。