机器人学中的状态估计学习笔记(二)第三章线性高斯系统的状态估计
3.1 离散时间的批量估计问题
3.1.1 问题定义
在离散时间线性时变系统中,定义运动和观测模型如下: 运 动 方 程 : x k = A k − 1 x k − 1 + v k + w k , k = 1 , . . . , K 运动方程:x_{k} =A_{k-1} x_{k-1} +v_{k} +w_{k} , k=1,...,K 运动方程:xk=Ak−1xk−1+vk+wk,k=1,...,K 观 测 方 程 : y k = C k x k + n k , k = 0 , . . . , K 观测方程:y_{k} =C_{k} x_{k} +n_{k} ,k=0,...,K 观测方程:yk=Ckxk+nk,k=0,...,K其中k为时间下标,最大值为K。各变量的含义如下: 系 统 状 态 : x k ∈ R N 系统状态:x_{k} \in \mathbb{R}^{N} 系统状态:xk∈RN 初 始 状 态 : x 0 ∈ R N ∼ N ( x ˇ 0 , P ˇ 0 ) ) 初始状态:x_{0} \in \mathbb{R}^{N} \sim N(\check{x}_{0},\check{P}_{0}) ) 初始状态:x0∈RN∼N(xˇ0,Pˇ0)) 输 入 : v k ∈ R N 输入:v_{k} \in \mathbb{R}^{N} 输入:vk∈RN 过 程 噪 声 : w k ∈ R N ∼ N ( 0 , Q k ) 过程噪声:w_{k} \in \mathbb{R}^{N} \sim N(0,Q_{k}) 过程噪声:wk∈RN∼N(0,Qk) 测 量 : y k ∈ R M 测量:y_{k} \in \mathbb{R}^{M} 测量:yk∈RM 测 量 噪 声 : n k ∈ R M ∼ N ( 0 , R k ) 测量噪声:n_{k} \in \mathbb{R}^{M} \sim N(0,R_{k}) 测量噪声:nk∈RM∼N(0,Rk)其中除了vk为确定性变量之外,其他的变量都是随机变量。噪声和初始状态一般假设互不相关的,并且在各个时刻与自己也互不相关。矩阵 A k ∈ R N × N A_{k} \in \mathbb{R} ^{N×N} Ak∈RN×N称为转移矩阵, C k ∈ R M × N C_{k} \in \mathbb{R} ^{M×N} Ck∈RM×N称为观测矩阵。
一般情况只知道以下几个变量,并根据它们来估计状态 x ^ k \hat{x} _{k} x^k:
- 初始状态 x ˇ 0 \check{x}_{0} xˇ0,以及相应的初始协方差矩阵 P ˇ 0 \check{P}_{0} Pˇ0。
- 输入量vk,通常来自控制器,是已知的;它的噪声协方差矩阵是Qk。
- 观测数据yk,meas是观测变量yk的一次实现,它的协方差为Rk。
状态估计问题是指:在k个(一个或多个)时间点上,基于初始的状态信息 x ˇ 0 \check{x}_{0} xˇ0、一系列观测数据y0:K,meas、一系列输入v1:K,以及系统的运动模型和观测模型,来计算系统的真实状态的估计值 x ^ k \hat{x} _{k} x^k
为了显示各个方法之间的联系,从两个不同的途径着手解决批量LG系统的估计问题:
- 贝叶斯推断。从状态的先验概率密度函数出发,通过初始状态、输入、运动方程和观测数据,计算状态的后验概率密度函数。
- 最大后验估计。采用优化理论,来寻找给定信息下(初始状态、输入、观测)的最大后验估计。
以上两种方法本质上是不同的,但在LG系统中,它们将给出同样的结论。主要原因在于,在LG系统中,贝叶斯后验概率正好是高斯的。所以优化方法会找到高斯分布的最大值(也就是它的模),这也正是高斯的均值。但在非线性非高斯系统中,一个分布的均值和模将不再重合,使得这两类方法给出不同的答案。
3.1.2 最大后验估计
在批量估计中,MAP的目标是求解这样一个问题: x ^ = a r g max x p ( x ∣ v , y ) \hat{x}=arg \underset{x}{\max} p(x|v,y) x^=argxmaxp(x∣v,y)也就是说,我们希望在给定先验信息和所有时刻的运动 v v v、观测 y y y 的情况下,推测出所有时刻的最优状态 x ^ \hat{x} x^。为此定义几个宏观变量: x = x 0 : K = ( x 0 , . . . , x K ) , v = ( x ˇ 0 , v 1 : K ) = ( x ˇ , v 1 , . . . , v K ) x=x_{0:K} =(x_{0} ,...,x_{K} ),v=(\check{x} _{0} ,v_{1:K} )=(\check{x} ,v_{1} ,...,v_{K} ) x=x0:K=(x0,...,xK),v=(xˇ0,v1:K)=(xˇ,v1,...,vK) y = y 0 : K = ( y 0 , . . . , y K ) y=y_{0:K} =(y_{0} ,...,y_{K} ) y=y0:K=(y0,...,yK) 首先,用贝叶斯公式重写MAP估计: x ^ = a r g max x p ( y ∣ x , v ) p ( x ∣ v ) p ( y ∣ v ) = a r g max x p ( y ∣ x ) p ( x ∣ v ) \hat{x} =arg\underset{x}{\max} \frac{p(y|x,v)p(x|v)}{p(y|v)} =arg\underset{x}{\max} p(y|x)p(x|v) x^=argxmaxp(y∣v)p(y∣x,v)p(x∣v)=argxmaxp(y∣x)p(x∣v)由于分母与x无关,将其略去。同时省略p(y|x,v)中的v,因为如果x已知,v不会影响观测数据。
接下来要做出一个重要的假设:对于所有时刻k=0,…,K,所有的噪声项 w k w_{k} wk和 n k n_{k} nk之间是无关的。这使得我们可以用贝叶斯公式对p(y|x)进行因子分解: p ( y ∣ x ) = ∏ k = 0 K p ( y k ∣ x k ) p(y|x)=\prod_{k=0}^{K}p(y_{k} |x_{k} ) p(y∣x)=k=0∏Kp(yk∣xk)另一方面,贝叶斯定理又允许我们将p(y|v)分解为: p ( x ∣ v ) = p ( x 0 ∣ x ˇ 0 ) ∏ k = 1 K p ( x k ∣ x k − 1 , v k ) p(x|v)=p(x_{0} |\check{x} _{0} )\prod_{k=1}^{K}p(x_{k} |x_{k-1},v_{k} ) p(x∣v)=p(x0∣xˇ0)k=1∏Kp(xk∣xk−1,vk)在线性系统中,高斯密度函数可展开为:
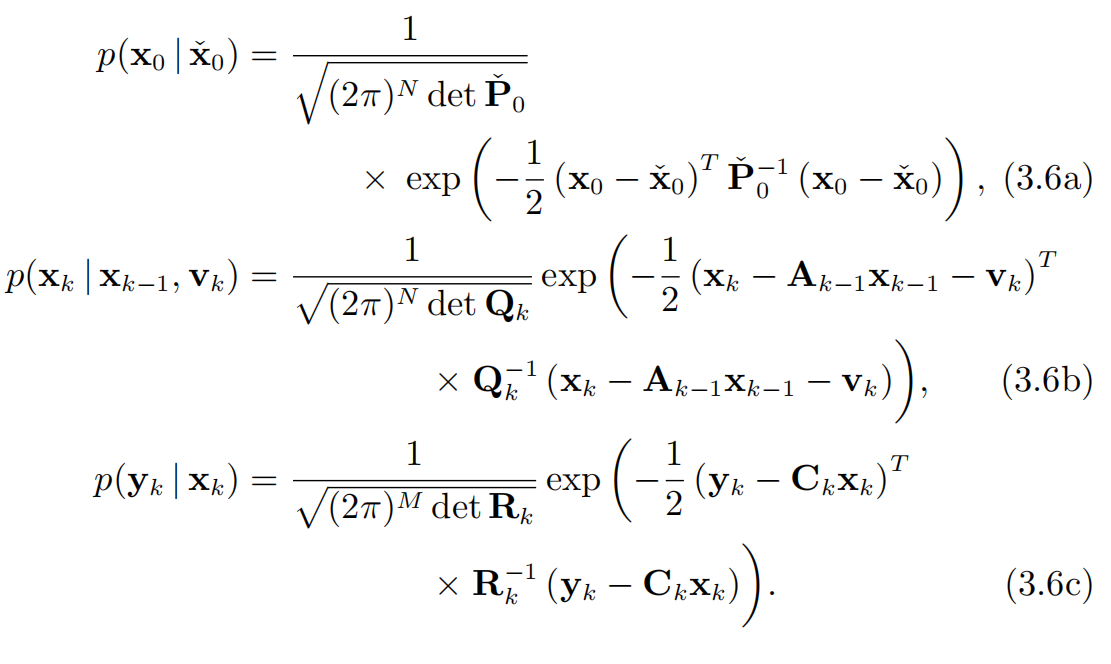
然后对等式两侧各取对数:

在这个过程中:

在式(3.8)中出现了一些与x无关的项,可以把它们忽略掉。因此,定义下面这些量:

这些都是平方马氏距离,所谓马氏距离表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是,它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的,即独立于测量尺度。对于一个均值为μ,协方差矩阵为Σ的多变量向量,其马氏距离为 ( x − μ ) T Σ − 1 ( x − μ ) \sqrt{(x-\mu )^{T}\Sigma ^{-1}(x-\mu )} (x−μ)TΣ−1(x−μ)。然后我们可以定义整体的目标函数 J ( x ) J(x) J(x)。通过最小化这个目标函数,我们来求解自变量x的值: J ( x ) = ∑ k = 0 K ( J v , k ( x ) + J y , k ( x ) ) J(x)=\sum_{k=0}^{K}(J_{v,k} (x)+J_{y,k} (x)) J(x)=k=0∑K(Jv,k(x)+Jy,k(x))从优化的角度来看,我们寻求下面这个优化问题的最优解: x ^ = a r g min x J ( x ) \hat{x} =arg\underset{x}{\min}J(x) x^=argxminJ(x)为了寻找最优状态估计,我们可以根据已有的数据计算最大似然估计。这个问题是一个无约束的优化问题,对于状态变量x本身并没有任何约束。
因为式(3.9)中所有的项都是x的二次形式,我们还可以进一步简化问题。把所有数据排成一列,称为提升形式。那么可以把所有时刻的状态组成一个向量x,并把所有时刻已知的数据组成一个向量 z z z: z = [ x ˇ 0 v 1 ⋮ v K ‾ y 0 y 1 ⋮ y K ] , x = [ x 0 ⋮ x K ] z=\begin{bmatrix} \check{x} _{0} \\ v_{1} \\ \vdots \\ \underline{ v_{K} } \\ y_{0} \\ y_{1} \\ \vdots\\ y_{K} \end{bmatrix},x=\begin{bmatrix} x_{0} \\ \vdots \\ x_{K} \end{bmatrix} z=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡xˇ0v1⋮vKy0y1⋮yK⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤,x=⎣⎢⎡x0⋮xK⎦⎥⎤然后,定义以下的块矩阵: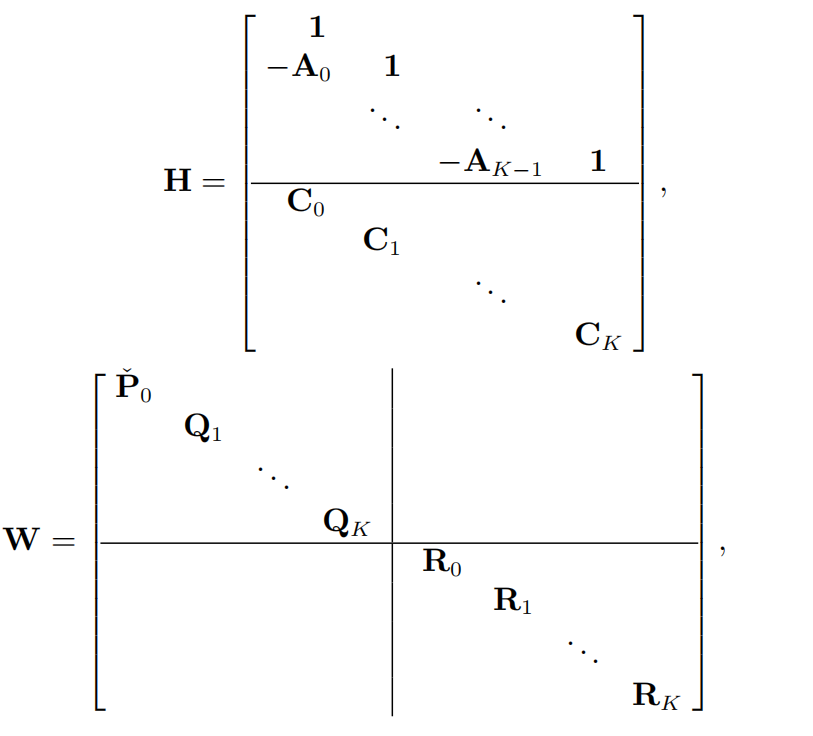
该式只显示了非零块,分割线用以区分矩阵的不同部分,例如先验信息、输入v、测量y以及提升形式的z。根据上面的定义,我们把目标函数写成: J ( x ) = 1 2 ( z − H x ) T W − 1 ( z − H x ) J(x)=\frac{1}{2} (z-Hx)^{T} W^{-1} (z-Hx) J(x)=21(z−Hx)TW−1(z−Hx)这正是x的二次形式。同时有: p ( z ∣ x ) = η e x p ( − 1 2 ( z − H x ) T W − 1 ( z − H x ) ) p(z|x)=\eta exp(-\frac{1}{2} (z-Hx)^{T} W^{-1} (z-Hx)) p(z∣x)=ηexp(−21(z−Hx)TW−1(z−Hx))其中 η \eta η为归一化因子。
因为 J ( x ) J(x) J(x)刚好是一个抛物面,可以解析地找到它的最小值。只需让目标函数相对于自变量的偏导数为0即可:
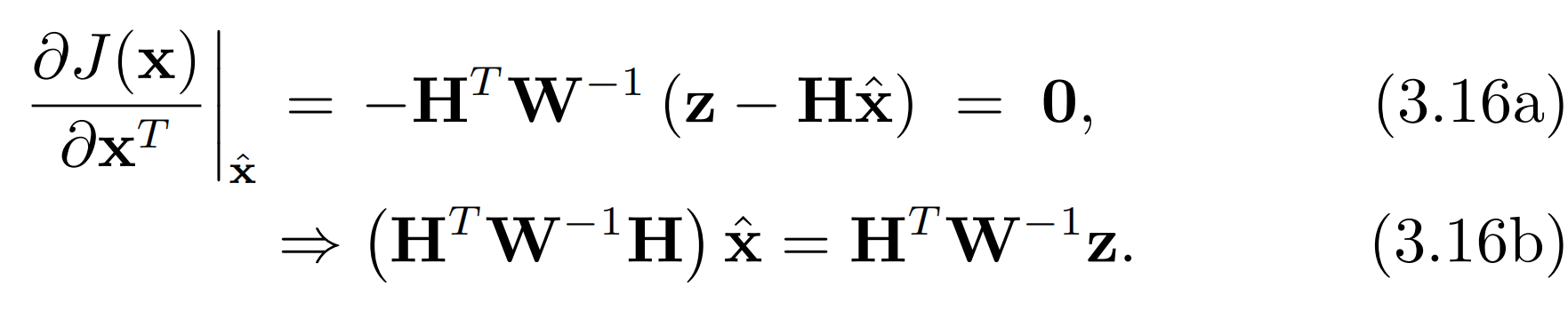
式(3.16)的解 x ^ \hat{x} x^ 是经典的批量最小二乘法的解。同时也等价于传统估计理论中的固定区间平滑算法批量最小二乘法的求解利用了矩阵求伪逆的方法。从计算角度来说,我们并不会真的去计算 H T W − 1 H H^{T} W^{-1} H HTW−1H的逆(即使它是个稠密矩阵)。由于 H T W − 1 H H^{T} W^{-1} H HTW−1H会有一种特殊的对角块结构,因此可以利用稀疏的求解算法来更高效地求解。
批量线性高斯系统的一种直观的解释,是把它看成一个弹簧-重物系统,如下图所示。最小二乘中的每一项代表了每个弹簧的能量,它和重物的位置有关。而最小二乘的最优解,就是整个系统处于最低能量的状态。

3.1.3 贝叶斯推断
在线性高斯系统中,全贝叶斯后验概率 p ( x ∣ v , y ) p(x|v,y) p(x∣v,y)的计算并不是简单地最大化它。需要从先验的概率密度函数出发,然后再用测量的数据来更新它。
在这个情况下,可以用初始状态和输入来建立状态的先验估计: p ( x ∣ v ) p(x|v) p(x∣v)。用运动方法来建立先验: x k = A k − 1 x k − 1 + v k + w k x_{k}=A_{k-1}x_{k-1}+v_{k}+w_{k} xk=Ak−1xk−1+vk+wk在提升形式中,可以写成: x = A ( v + w ) x=A(v+w) x=A(v+w)这里 w w w也是初始状态和运动噪声的提升形式,同时,

是转移矩阵的提升形式,可见它是下三角的。于是,提升之后的均值为: x ˇ = E [ x ] = E [ A ( v + w ) ] = A v \check{x} =E[x]=E[A(v+w)]=Av xˇ=E[x]=E[A(v+w)]=Av提升的协方差为: P ˇ = E [ ( x − E [ x ] ) ( x − E [ x ] ) T ] = A Q A T \check{P} =E[(x-E[x])(x-E[x])^{T} ]=AQA^{T} Pˇ=E[(x−E[x])(x−E[x])T]=AQAT其中 Q = E [ w w T ] = d i a g ( P 0 , Q 1 , . . . , Q K ) Q=E[ww^{T} ]=diag(P_{0} ,Q_{1} ,...,Q_{K} ) Q=E[wwT]=diag(P0,Q1,...,QK)。那么,先验就可以简洁地写成: p ( x ∣ v ) = N ( x ˇ , P ˇ ) = N ( A v , A Q A T ) p(x|v)=N(\check{x} ,\check{P} )=N(Av,AQA^{T} ) p(x∣v)=N(xˇ,Pˇ)=N(Av,AQAT)再来看观测。观测模型为: y k = C k x k + n k y_{k}=C_{k}x_{k}+n_{k} yk=Ckxk+nk写成提升形式: y = C x + n y=Cx+n y=Cx+n其中n是提升之后的测量噪声,且 C = d i a g ( C 0 , C 1 , . . . , C K ) C=diag(C_{0} ,C_{1} ,...,C_{K} ) C=diag(C0,C1,...,CK)是提升后的观测矩阵。于是,提升之后的状态、观测联合概率密度函数可写成:
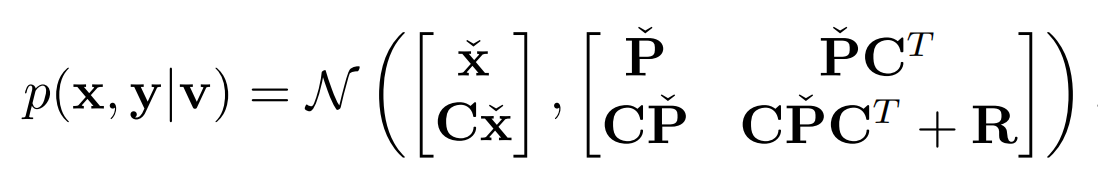
这里 R = E [ n n T ] = d i a g ( R 0 , R 1 , . . . , R K ) R=E[nn ^{T}]=diag(R_{0},R_{1},...,R_{K}) R=E[nnT]=diag(R0,R1,...,RK)。这个式子因式分解: p ( x , y ∣ v ) = p ( x ∣ v , y ) p ( y ∣ v ) p(x,y|v)=p(x|v,y)p(y|v) p(x,y∣v)=p(x∣v,y)p(y∣v)我们只关心第一个因子,它表示了全贝叶斯后验概率。这一项根据上一节的式(2.53) p ( x ∣ y ) = N ( μ x + Σ x y Σ y y − 1 ( y − μ y ) , Σ x x − Σ x y Σ y y − 1 Σ y x ) p(x|y)=N(\mu _{x} +\Sigma _{xy} \Sigma_{yy}^{-1}(y-\mu_{y}),\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}) p(x∣y)=N(μx+ΣxyΣyy−1(y−μy),Σxx−ΣxyΣyy−1Σyx)可以重写成:
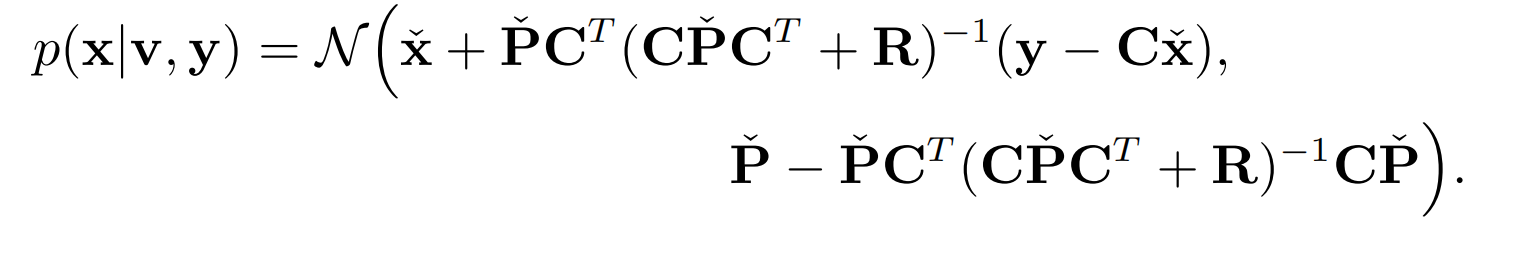
利用SMW恒等式,可将上式转换成:
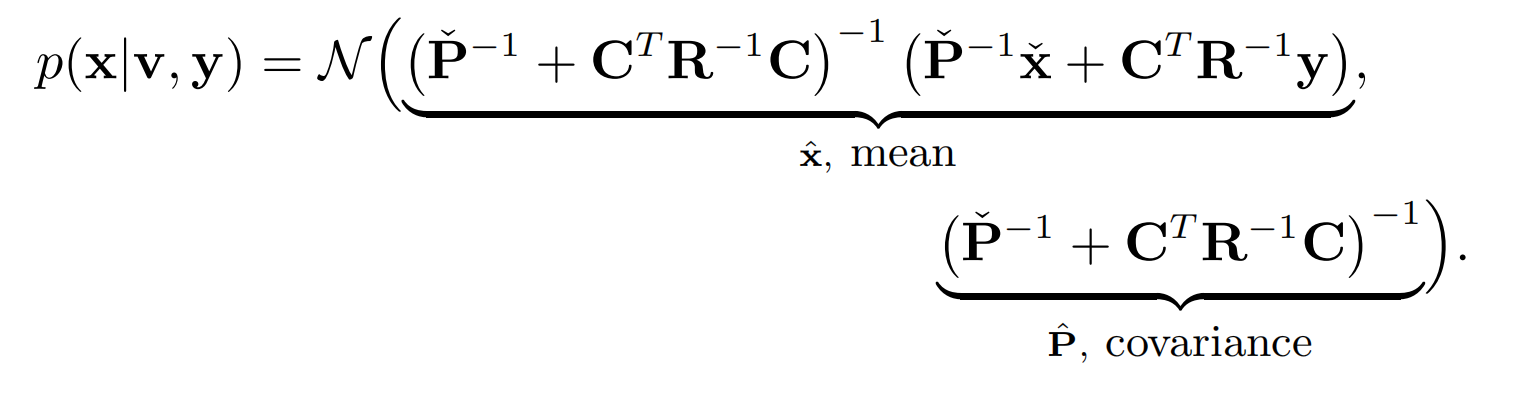
事实上,基于这个等式就能实现一个贝叶斯估计器,因为它代表了全贝叶斯后验概率,但这种做法并不高效。
为显示此方法与之前讲的优化方法的联系,整理均值项,让他成为 x ^ \hat{x} x^的线性函数:

可见,左侧出现了先验的协方差的逆。代入 x ˇ = A v \check{x} =Av xˇ=Av和 P ˇ − 1 = ( A Q A T ) − 1 = A − T Q − 1 A − 1 \check{P}^{-1}=(AQA^{T})^{-1}=A^{-T}Q^{-1}A^{-1} Pˇ−1=(AQAT)−1=A−TQ−1A−1,可以将它重写成:

这里需要计算 A − 1 A^{-1} A−1,不过它正好有个漂亮的形式:
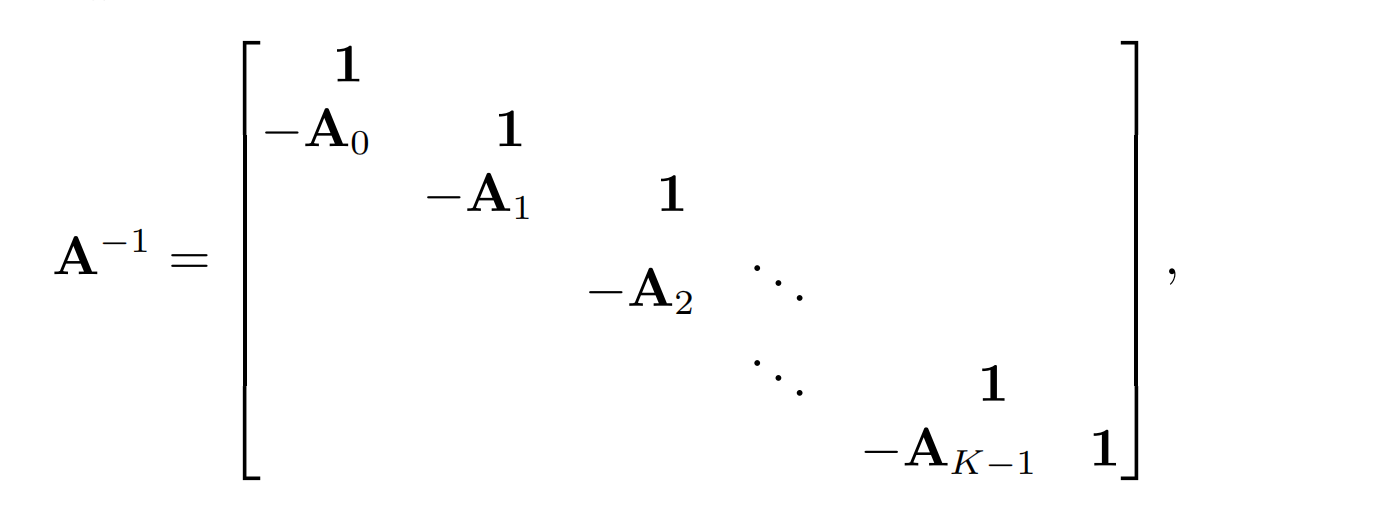
它仍是个下三角矩阵,但形式非常稀疏(仅有主对角线和下方的一块非零)。如果定义:
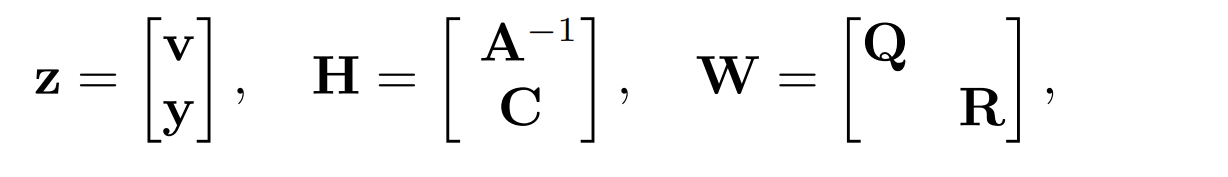
就可以把系统写成: ( H T W − 1 H ) x = H T W − 1 z {\color{Red} (H^{T} W^{-1} H)x=H^{T} W^{-1} z} (HTW−1H)x=HTW−1z这和之前讨论的最优化方法的解完全一致。
在线性高斯系统中,贝叶斯推断给出了与优化方法(最大后验估计)一致的解,本质上是因为线性高斯系统的贝叶斯后验概率仍是高斯的,而高斯函数的均值和模是一样的。
3.1.4 存在性、唯一性与能观性
从基本的线性代数可以看出,当且仅当 H T W − 1 H H^{T} W^{-1} H HTW−1H可逆时, x ^ \hat x x^存在且唯一。那么: x ^ = ( H T W − 1 H ) − 1 H T W − 1 z \hat x=(H^{T} W^{-1} H)^{-1}H^{T} W^{-1} z x^=(HTW−1H)−1HTW−1z于是,问题就变为,何时 H T W − 1 H H^{T} W^{-1} H HTW−1H可逆?再从基本的线性代数来看,因为 d i m x = N ( K + 1 ) dim x =N(K+1) dimx=N(K+1),所以可逆的充要条件是: r a n k ( H T W − 1 H ) = N ( K + 1 ) rank(H^{T} W^{-1} H)=N(K+1) rank(HTW−1H)=N(K+1)又因为 W − 1 W^{-1} W−1是实对称且正定的,所以可以仅检测: r a n k ( H T H ) = r a n k ( H T ) = N ( K + 1 ) rank(H^{T} H)=rank(H^{T} )=N(K+1) rank(HTH)=rank(HT)=N(K+1)即要求 H T H^{T} HT有N(K+1)个线性无关的行/列向量。
接下来,分为情况两种进行讨论:
1.初始状态有先验信息: x ˇ 0 \check x_{0} xˇ0;
2.初始状态没有先验信心。
情况1:有先验
将 H T H^{T} HT展开,我们需要检测秩的矩阵为:
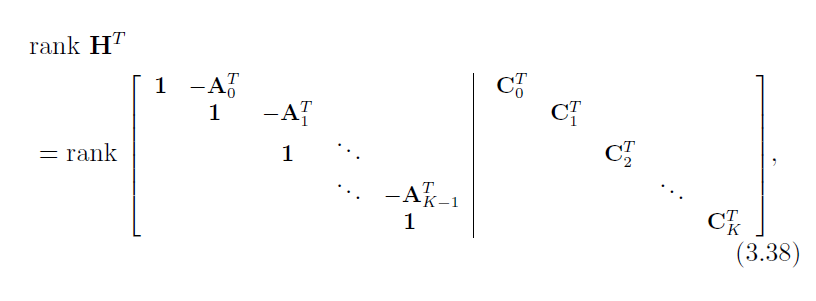
这是一个阶梯形矩阵。显然它每一行都是线性无关的,这意味着该矩阵是满秩的。所以,我们能够得到一个唯一解 x ^ \hat x x^ ,只须: P 0 ˇ > 0 , Q k > 0 \check{P_{0}}>0,Q_{k}>0 P0ˇ>0,Qk>0这里>0意味着矩阵是正定的(因此也是可逆的)。直观上说,因为先验已经给出了系统的一个解,我们只是用观测来修正它。这只是充分但不是必要的条件。
情况2:没有先验知识
H T H^{T} HT中每一列中的块都表示了一部分有关系统的信息,而第一列的块表达了我们对初始状态信息的了解程度。因此,去掉第一列之后,变为:

这个矩阵有K+1个行(每块大小为N)。将最上一行移到最小(这不会改变矩阵的秩),得:
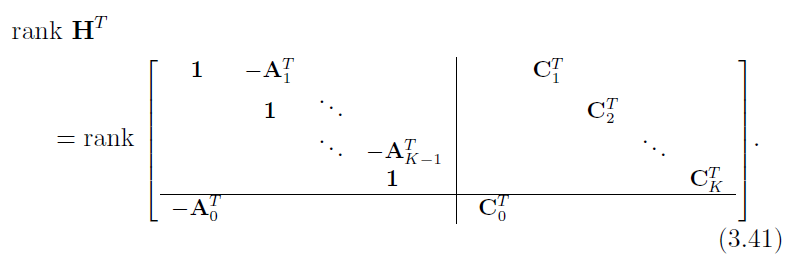
那么,除去最后一行,这个矩阵仍是阶梯形矩阵。同理,在不影响秩得前提下,我们可以用 A 0 T A_{0}^{T} A0T乘第一行,然后加到最后一行上;再用 A 0 T A 1 T A_{0}^{T}A_{1}^{T} A0TA1T乘第二行,加到最后一行上…最后用 A 0 T A 1 T . . . A K − 1 T A_{0}^{T}A_{1}^{T}...A_{K-1}^{T} A0TA1T...AK−1T乘倒数第二行,加到最后一行,得到:
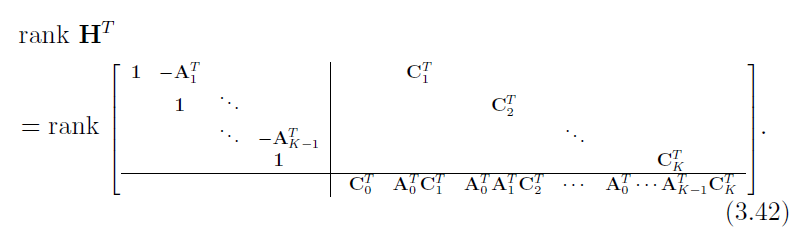
检查最终的表达式,可见左下角块为0,同时,左上角块是阶梯形矩阵,所以是满秩的(每一行有一个领头的非零块)。于是,对 H T H^{T} HT的秩判定,归结于右下角部分是否为秩N:
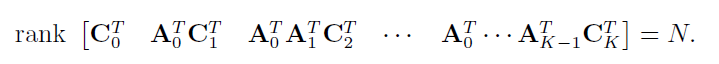
如果进一步假设系统是时不变的,那么对所有的k,有 A k = A , C k = C A_{k}=A,C_{k}=C Ak=A,Ck=C,并且做一个不那么严格的假设:K >>N,之后还能进一步简化这个条件。
为了做这件事,需要引入线性代数中的卡莱-哈密顿定理。因为A是N×N的,它的特征方程最多有N项,因此A的大于等于N次以上的高阶项必能写成 1 , A , . . . , A N − 1 1,A,...,A^{N-1} 1,A,...,AN−1的一种线性组合。展开来说,对于 ∀ k ≥ N \forall k\ge N ∀k≥N,能够找到一组不全为零的系数 a 0 , a 1 , . . . , a N − 1 a_{0},a_{1},...,a_{N-1} a0,a1,...,aN−1,使得
又因为矩阵的行秩和列秩是一样的,因而:
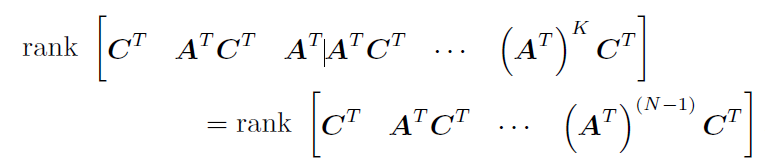
定义能观性矩阵 O \mathcal{O} O 为:
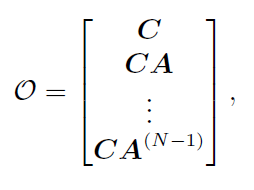
那么秩条件就简化为: r a n k O = N rank\mathcal{O}=N rankO=N这就是能观性矩阵的判别条件。在此指明了系统能观性和 H T W − 1 H H^{T}W^{-1}H HTW−1H可逆性之间的联系。总而言之,使得解是存在且唯一的条件是: Q k > 0 , R k > 0 , r a n k O = N Q_{k}>0,R_{k}>0,rank\mathcal{O}=N Qk>0,Rk>0,rankO=N 这里大于0的意思是矩阵正定(因而可逆)。这些仍是充分条件而非必要条件。
解释
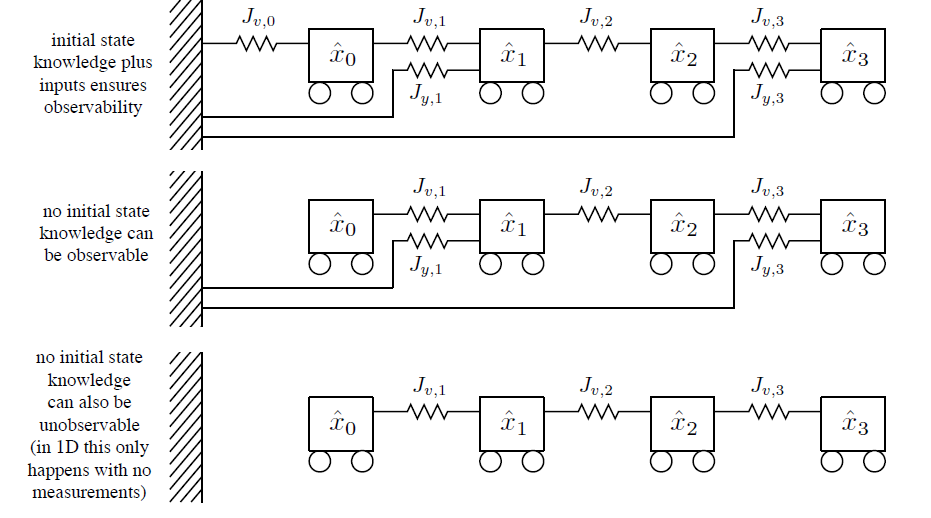
仍然回到弹簧-质点模型,来理解能观性方面的问题。如下图展现了一些例子。当我们有初始状态时(顶上的图例),系统总是能观的,因为你没法在不改变(至少一个)弹簧长度的条件下,移动任意一个(或多个)重物。也就是说,这样一个系统有一个唯一的最小能量状态。对于中间的例子,结论也是一样,即使我们不知道初始状态。最下面的例子则是不能观的,因为我们可以把所有重物任意左移或右移,同时不改变弹簧储存的能量。这样一个系统的最小能量就是不唯一的。
3.1.5 MAP的协方差
回到式 x ^ = ( H T W − 1 H ) − 1 H T W − 1 z \hat x=(H^{T} W^{-1} H)^{-1}H^{T} W^{-1} z x^=(HTW−1H)−1HTW−1z, x ^ \hat x x^表示了状态真值x最可能的估计。那么另一个重要的问题是说,我们对 x ^ \hat x x^的置信度如何?也就是说,我们可以用高斯形式对最小二乘解作另一种解释: ( H T W − 1 H ) ⏟ 协 方 差 的 逆 x ^ ⏟ 均 值 = H T W − 1 z ⏟ 信 息 向 量 \underset{协方差的逆}{\underbrace{(H^{T} W^{-1} H)} }\underset{均值}{\underbrace{ \hat x}} =\underset{信息向量}{\underbrace{H^{T} W^{-1} z} } 协方差的逆
(HTW−1H)均值
x^=信息向量
HTW−1z等式右侧称为信息向量。为了说明它的含义,用贝叶斯法则重写式子 p ( z ∣ x ) = η e x p ( − 1 2 ( z − H x ) T W − 1 ( z − H x ) ) p(z|x)=\eta exp(-\frac{1}{2} (z-Hx)^{T} W^{-1} (z-Hx)) p(z∣x)=ηexp(−21(z−Hx)TW−1(z−Hx))为: p ( x ∣ z ) = β e x p ( − 1 2 ( H x − z ) T W − 1 ( H x − z ) ) p(x|z)=\beta exp(-\frac{1}{2} (Hx-z)^{T} W^{-1}(Hx-z)) p(x∣z)=βexp(−21(Hx−z)TW−1(Hx−z))这里 β \beta β 是归一化因子。然后把式子 x ^ = ( H T W − 1 H ) − 1 H T W − 1 z \hat x=(H^{T} W^{-1} H)^{-1}H^{T} W^{-1} z x^=(HTW−1H)−1HTW−1z代入并作一些简化,易得: p ( x ∣ x ^ ) = κ e x p ( − 1 2 ( x − x ^ ) T ( H T W − 1 H ) ( x − x ^ ) ) p(x|\hat{x})=\kappa exp(-\frac{1}{2} (x-\hat{x})^{T} (H^{T}W^{-1}H)(x-\hat{x})) p(x∣x^)=κexp(−21(x−x^)T(HTW−1H)(x−x^))这里 κ \kappa κ也是一个归一化因子。从该式可以看出, N ( x ^ , P ^ ) N(\hat{x} ,\hat{P}) N(x^,P^)是最小二乘算法对x的高斯估计,其中均值即最优解,而协方差 P ^ = ( H T W − 1 H ) − 1 \hat{P}=(H^{T} W^{-1} H)^{-1} P^=(HTW−1H)−1。
另一种处理方式是直接对最优解取期望。注意: x − ( H T W − 1 H ) − 1 H T W − 1 z ⏟ E [ x ] = ( H T W − 1 H ) − 1 H T W − 1 ( H x − z ) ⏟ s z x-\underset{E[x]}{\underbrace{(H^{T} W^{-1} H)^{-1}H^{T} W^{-1}z} } =(H^{T} W^{-1} H)^{-1}H^{T} W^{-1}\underset{s}{\underbrace{(Hx-z)} } z x−E[x]
(HTW−1H)−1HTW−1z=(HTW−1H)−1HTW−1s
(Hx−z)z其中 s = [ w n ] s=\begin{bmatrix} w \\ n\end{bmatrix} s=[wn]那么就有: p ^ = E [ ( x − E [ x ] ) ( x − E [ x ] ) T ] \hat{p} =E[(x-E[x])(x-E[x])^{T}] p^=E[(x−E[x])(x−E[x])T] = ( H T W − 1 H ) − 1 H T W − 1 E [ s s T ] ⏟ W W − 1 H ( H T W − 1 H ) − 1 =(H^{T} W^{-1} H)^{-1}H^{T} W^{-1}\underset{W}{\underbrace{E[ss^{T}]} } W^{-1}H(H^{T}W^{-1}H)^{-1} =(HTW−1H)−1HTW−1W
E[ssT]W−1H(HTW−1H)−1 = ( H T W − 1 H ) − 1 =(H^{T} W^{-1} H)^{-1} =(HTW−1H)−1仍能得到上述的结论。
小结
总的来说,离散时间批量估计的方法主要有最大后验估计和贝叶斯推断两种方法。由于线性高斯系统中贝叶斯后验概率仍是高斯的,所以高斯函数的均值和模都是一样,因此,该两种方法最终得到的解是一致的,都为 x ^ = ( H T W − 1 H ) − 1 H T W − 1 z \hat x=(H^{T} W^{-1} H)^{-1}H^{T} W^{-1} z x^=(HTW−1H)−1HTW−1z。
3.2 离散时间的递归平滑算法
本小节主要是介绍了两种递归平滑算法,分别是Cholesky平滑算法和Rauch-Tung-Striebel平滑算法。该两种方法都利用了上一节批量优化结论中国的稀疏结构 H T W − 1 H H^{T}W^{-1}H HTW−1H(三对角块)来加速方程的求解。采用前向-后向的递归操作来完成。
在Cholesky平滑算法中,利用上一节的核心等式 ( H T W − 1 H ) x ^ = H T W − 1 z (H^{T} W^{-1} H)\hat x=H^{T} W^{-1} z (HTW−1H)x^=HTW−1z,然后主要分为三个步骤:
- 令 H T W − 1 H = L L T H^{T}W^{-1}H=LL^{T} HTW−1H=LLT,先求解出L;
- 令 d = L T x ^ , 求 L d = H T W − 1 d=L^{T}\hat x,求Ld=H^{T} W^{-1} d=LTx^,求Ld=HTW−1,求解出d;
- 最后根据 d = L T x ^ d=L^{T}\hat x d=LTx^,求解 x ^ \hat x x^。
以上前两个步骤为前向迭代过程,第三步为后向迭代过程。最终得到如下的递归方程: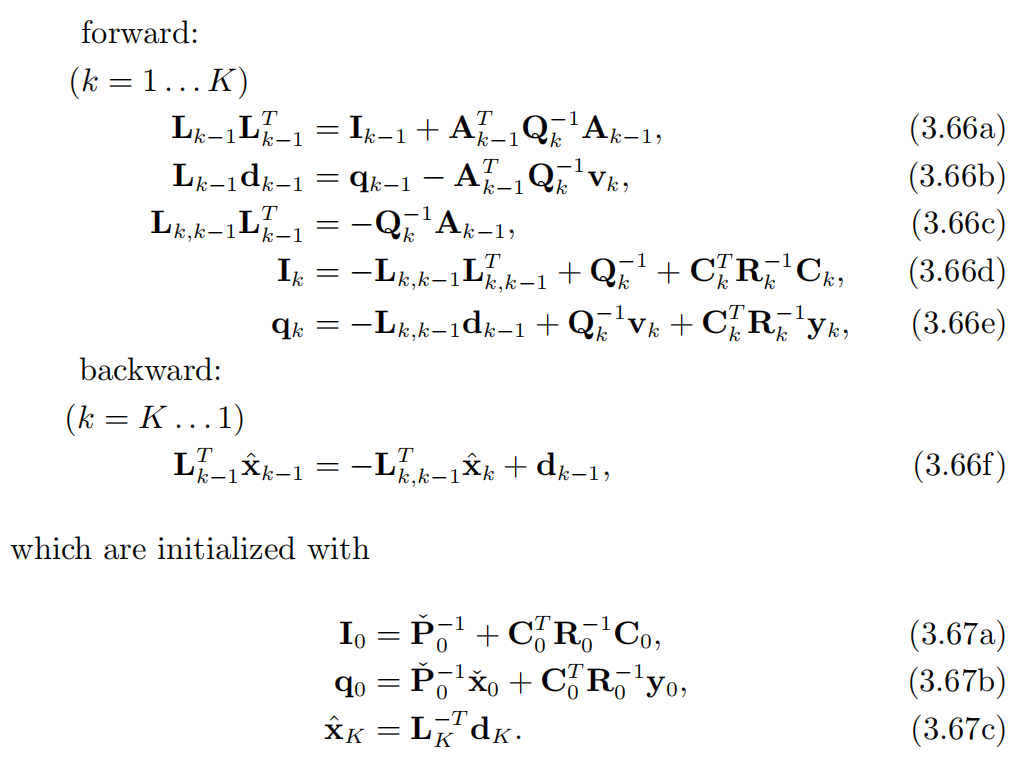
以上的六个递归方程等价于传统的Rauch-Tung-Striebel(RST)平滑算法;而5个前向迭代方程则等价于著名的卡尔曼滤波器。
实际上,RTS平滑算法是比Cholesky平滑算法更为标准的方程形式,通过代数运算,得到更经典的表达形式。利用SMW等式来进行代数操作,并且在化简得过程中,令 P ^ k , f = I k − 1 , P ^ k , f − 1 x ^ k , f = q k \hat P_{k,f}=I_{k}^{-1},\hat P_{k,f}^{-1}\hat x_{k,f}=q_{k} P^k,f=Ik−1,P^k,f−1x^k,f=qk,并定义卡尔曼增益 K k = P ^ k , f C k T R k − 1 K_{k}=\hat P_{k,f}C_{k}^{T}R_{k}^{-1} Kk=P^k,fCkTRk−1,最终根据cholesky平滑算法的6个递归方程,通过一系列得代数操作,得到以下的RTS平滑算法:
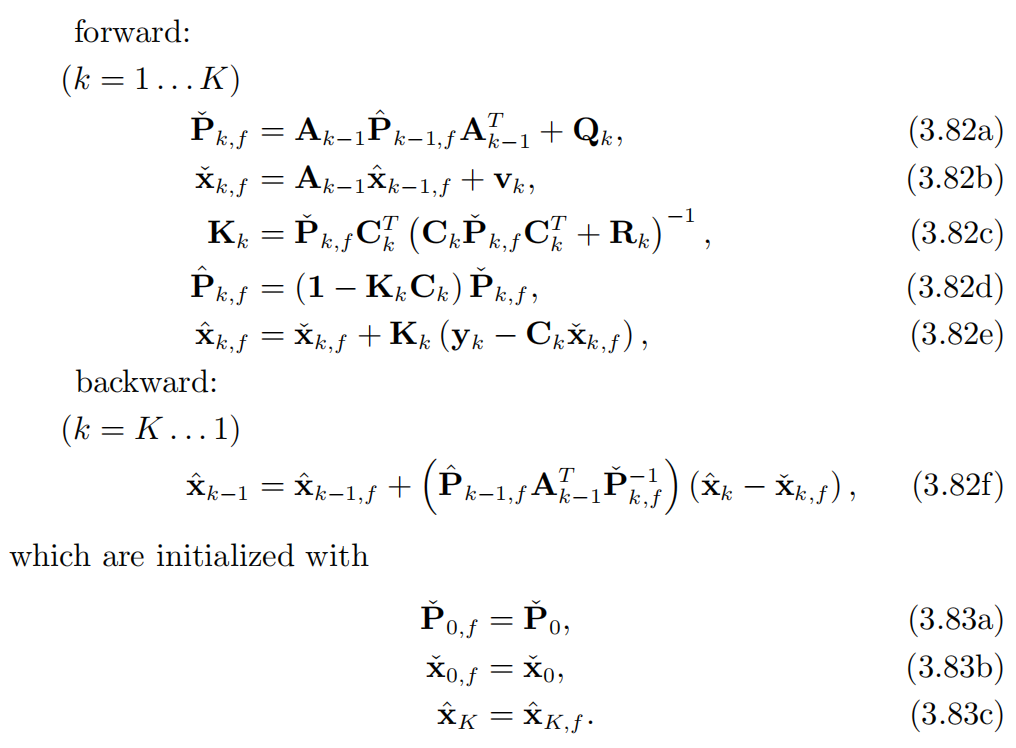
其中前五个前向迭代过程被称为经典的卡尔曼滤波器,更重要的是,以上6个公式表达的RTS平滑算法,能够高效且无近似地解决之前提到的批量优化问题。这件事情成立的原因正是由于优化算法左侧矩阵的特殊三对角块的稀疏结构,和批量解法本质上是一样的。
总的来说,该两种平滑算法都利用了所有能用到的数据来估计所有时刻的状态。
3.3 离散时间的递归滤波算法
为了解决上文介绍的批量优化和平滑算法无法在线运行的问题,因为它需要用到未来时刻的信息估计过去的状态,因此为了在实时场合使用,当前的状态只能由之前时间的信息决定,而卡尔曼滤波就是对这样的问题的传统解决方案。在上一节的RTS平滑算法的前向迭代过程中已经引出了卡尔曼滤波。本节将介绍其他几种推导卡尔曼滤波的方法。

首先对上一节批量优化得到的结果分解成前向递归估计和后向递归估计,为了实现这一结果需要将 z , H , W z,H,W z,H,W按不同时刻来重新排列,最终得到等式:
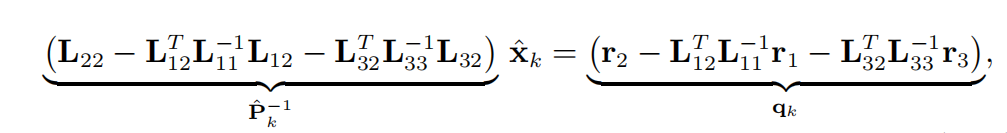
其中:
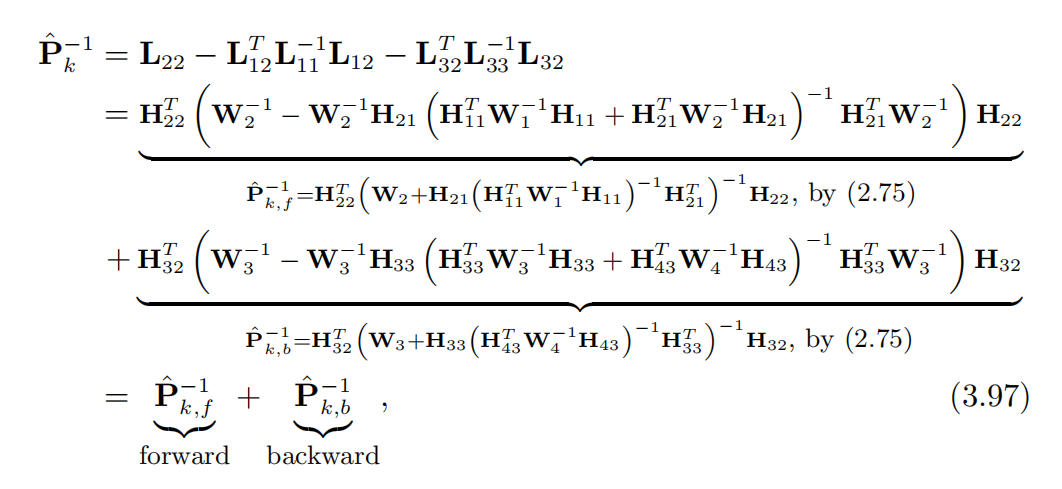
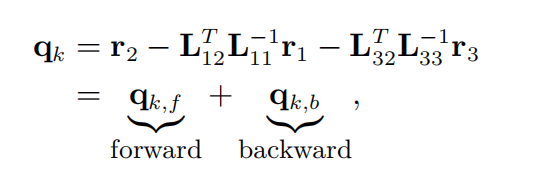
通过化简 P ^ k − 1 \hat P_{k}^{-1} P^k−1和 q k q_{k} qk分为了前向过程和后向过程,前向过程仅用k时刻以前的H和W块,后向过程仅用到k+1至K时刻的H与W块。
于是,分别得到“前向”和“后向”的估计器,分别计算 x ^ k , f \hat x_{k,f} x^k,f和 x ^ k , b \hat x_{k,b} x^k,b:

进一步的化简得到:
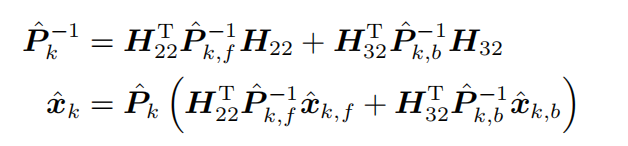
最终通过高斯密度函数的归一化积,得到:
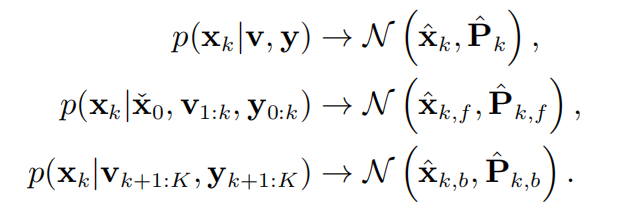
然后是采用MAP方法、贝叶斯推断方法分别将前向的高斯估计 x ^ k , f \hat x_{k,f} x^k,f推导出递归滤波器器,也就是卡尔曼滤波器。
在MAP方法中采用了消元法将不关心的变量边缘化掉,并通过SMW恒等式变换和一系列的化简最终求解出递归滤波如下:
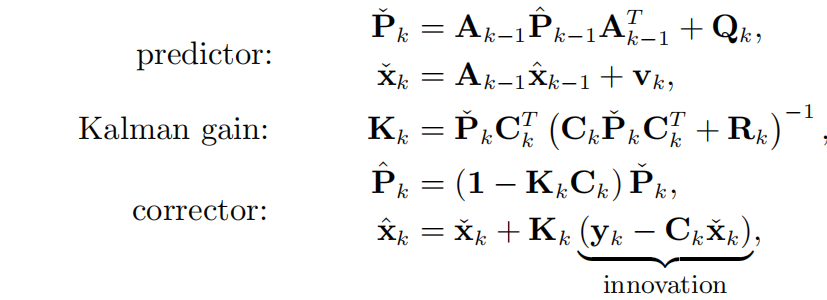
在贝叶斯推断方法中,则以更加简洁的方式推出卡尔曼滤波。通过联合高斯推断推导出均值和协方差,最终求得:

这与MAP给出的更新步骤的方程式完全一致的。根本原因在于采用的是线性模型,而噪声和先验也都是高斯的。在这些条件下,后验概率亦是高斯的,于是它的均值和模也是一样的。但在非线性模型中就不能保证这个性质了。
然后是从增益最优化的角度来看卡尔曼滤波,选取合适的 K k K_{k} Kk值,正确地衡量修正部分的权重。

并定义状态的误差为 e ^ k = x ^ k − x k \hat e_{k} =\hat x_{k} -x_{k} e^k=x^k−xk,以及代价函数 J ( K k ) = 1 2 t r E [ e ^ k e ^ k T ] J(K_{k})=\frac{1}{2} trE[\hat{e}_{k} \hat{e}_{k}^{T}] J(Kk)=21trE[e^ke^kT]。
最终求解 K k K_{k} Kk为: K k = P ˇ k C k T ( C k P ˇ k C k T + R k ) − 1 K_{k}=\check P_{k}C_{k}^{T}(C_{k} \check P_{k}C_{k}^{T}+R_{k})^{-1} Kk=PˇkCkT(CkPˇkCkT+Rk)−1关于卡尔曼滤波的要点如下:
1.对于高斯噪声的线性系统,卡尔曼滤波器是最优线性无偏估计。这意味着它给出的解的协方差矩阵正位于克拉美罗下界处;
2.必须有初始状态:{
x ˇ 0 , P ˇ 0 \check x_{0},\check P_{0} xˇ0,Pˇ0};
3.协方差部分与均值部分可以独立地递推。有时可以计算一个固定的 K k K_{k} Kk,用于所有时刻的均值修正。这种做法称为固定状态的卡尔曼滤波;
4.实现当中我们必须用实际的 y k , m e a s y_{k,meas} yk,meas,它们来自传感器的实际读数;
5.从后向过程一样能推导出类似的滤波方法,这种方法沿着时间反向递归。