目录
前两章云里雾里的开飞机过来的，就让前两章随风而去，第三章才是正轨。
第三章、线性模型
3.1、基本形式
这上面没什么可说的，就是一个函数，向量形式w进行转置，右乘x，加上b。
3.2、线性回归
开始之前，明白一点，数据集中有很多样本，每个样本输出一个x值，一定会有一个值y值与之对应。就会呈现一条线y=kx+b , 所有的（x，y）点都在这一条线附近，也有可能在线上。每个在这条线附近的点垂直到这条线，叫做欧氏距离，把所有的附近的点垂直的距离相加，得出一个最小值，那么就可以说这条线是最理想的。
引用相同的思想，线性回归等式，下面有写。
我们先考虑一种最简单的情形:输入属性的数目只有一个.为便于讨论,此时我们忽略关于属性的下标,若属性值间存在“序”(order)关系,可通过连续化将其转化为连续值,例如二值属性“身高”的取值“高”“矮”可转化为{1.0,0.0}, 三值属性“高度”的取值“高”“中”“低”可转化为{1.0,0.5,0.0};若属性值间不存在序关系,假定有k个属性值,则通常转化为k维向量,例如属性“瓜类”的取值“西瓜”“南瓜”“黄瓜”可转化为(0,0,1),(0,1,0),(1,0,0)。
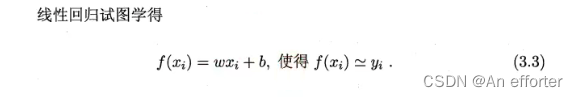
只有知道w和b才能得出线性方程，如何确定w和b呢? 显然,关键在于如何衡量f(x)与y之间的差别。2.3节介绍过,均方误差(2.2)是回归任务中最常用的性能度量,因此我们可试图让均方误差最小化,即
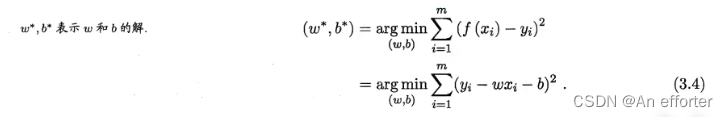
3.4式展开显示：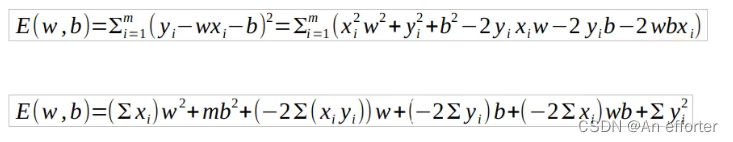 
对于以上公式的几何：
均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称“欧氏距离”(Euclidean distance).基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method).在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
因为我们肯定是想要最好的结果，所以要误差最小。要的是以下最小点，在几何图中如下图这样表示：
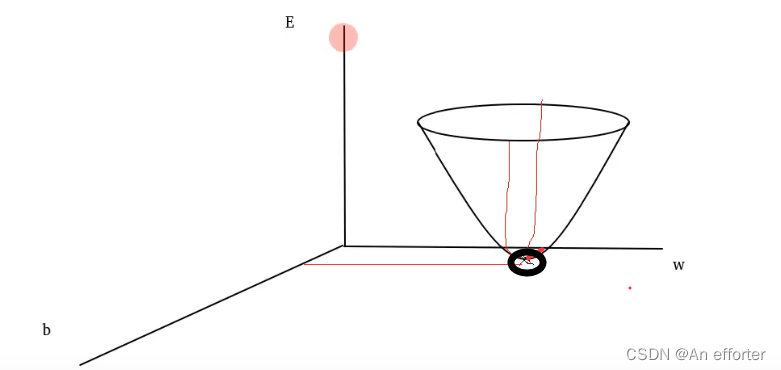
在数学中的表示就是对w与b的偏导：令偏导等于0，因为最下面的点平行于w和b轴。所以能求出w与b。
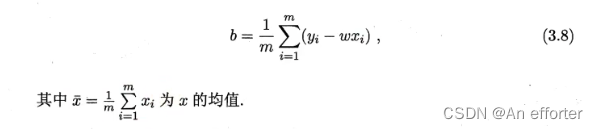
类似的，可利用最小二乘法来对w和b进行估计.为便于讨论,我们把w和b吸收入向量形式w_hat =(w; b),相应的,把数据集D表示为一个m *(d+ 1)大小的矩阵X，其中每行对应于一个示例,该行前d个元素对应于示例的d个属性值,最后一个元素恒置为1,即
把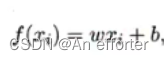 
写成矩阵形式，X是上面的形式，代入得出：
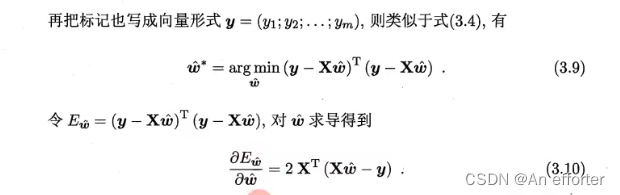
这里的公式推导西瓜书公式详解上有。
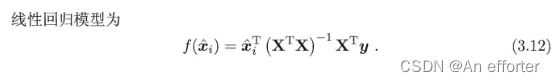
引出对数线性回归：
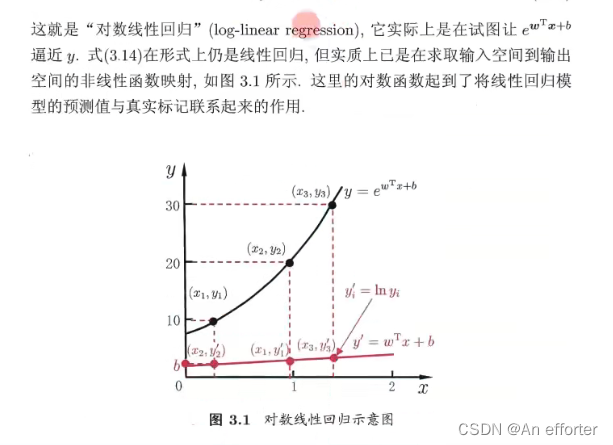
3.3对数几率回归
引入这个概念是因为线性回归中的f（x）的值域是R，考虑二分类任务，其输出标记y属于{0，1}，也就是值域映射到0-1之间。
1.从线性回归到对数几率回归的过程
线性回归模型产生的预测值
的实值，于是我们需要将实值z转化位0/1值，最理想的是“单位阶跃函数”。
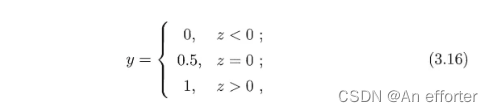
即若预测值z大于零就判为正例,小于零则判为反例,预测值为临界值零则可任意判别,如图3.2所示.
所以我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”(surrogate function)，并希望它单调可微.
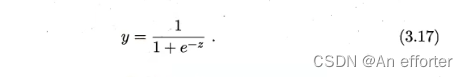
从图3.2可看出,对数几率函数是一种“Sigmoid函数”,它将z值转化为一个接近0或1的y值，并且其 输出值在z=0附近变化很陡。 将代入：
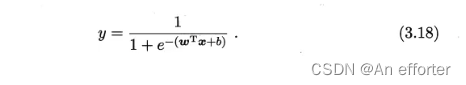
这样一折射为二分类的任务，那么就有了二分类的正负问题，正的概率P就属于了(0,1)之间，反之负的概率就是（1- P）。
下面我们来看看如何确定式(3.18)中的w和b.若将式(3.18)中的 y 视为类后验概率估计p(y= 1| x),则式(3.19)可重写为
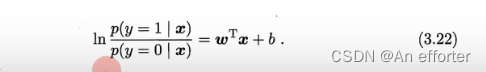
2.最大似然估计
我们用最大似然估计来估计w和b。
第一步:确定概率质量函数（概率密度函数)
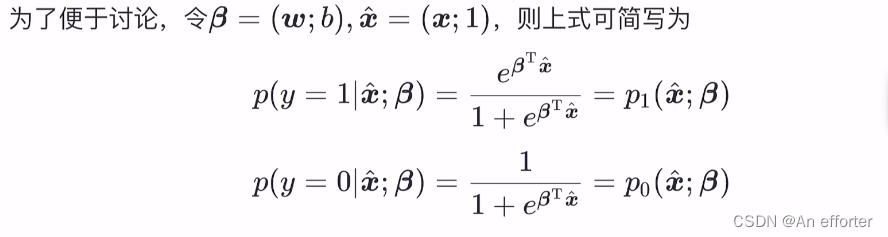
以上化简是按照矩阵的方式，得出的结果。
由以上的概率值可以推出随机变量y属于{0,1}的概率质量函数为
第二步：写出似然函数
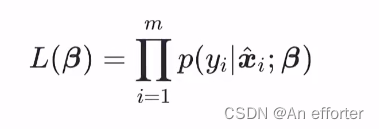
似然函数加一个ln ,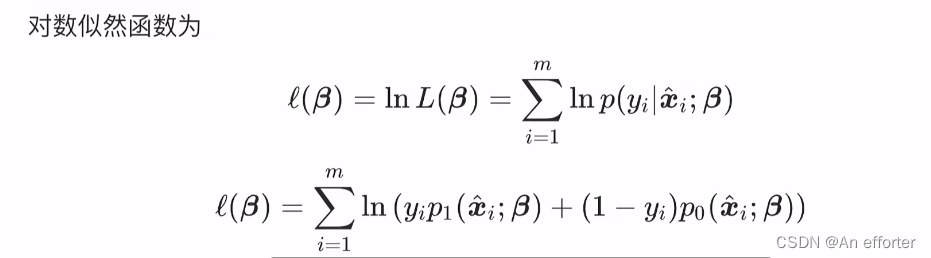
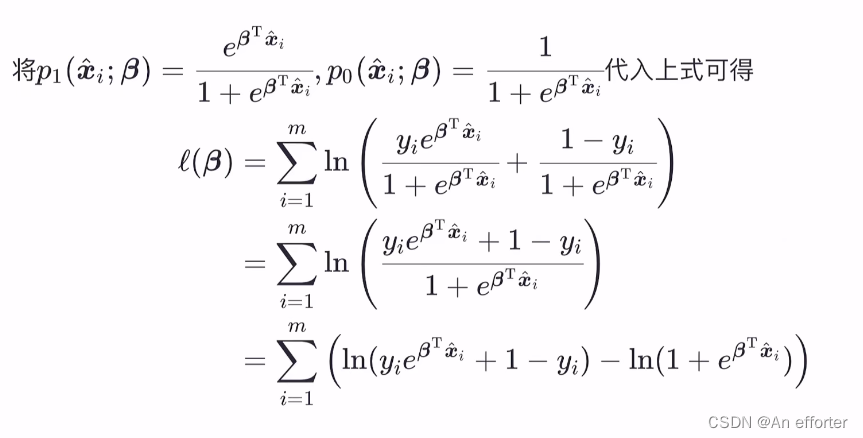
第三步：从似然函数到损失函数：
3.4线性判别分析
1.基本原理
线性判别分析简称问LDA，它的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别.图3.3给出了一个二维示意图.
从几何的角度，让全体训练样本经过投影后:
- 异类样本的中心尽可能远
- 同类样本的方差尽可能小
2.损失函数推导
第一个要求： 
和
是两类样本的投影到目标线上的距离，夹角
和
是两类样本原点到目标线与目标线的夹角。 上面的公式是求两类样本点的距离，尽可能远。
第二个要求：经过投影后，同类样本的方差尽可能小，
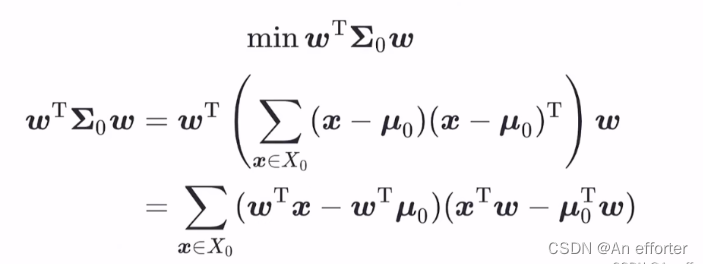
代表样本在w方向的投影长度-样本中线点在w方向的投影长度。可以理解为在w方向的两个坐标，后面的等式一个意思，那么就看成立
两种样本相间的距离尽可能远推导公式：
二范数就是求模长就是以下这种形式：
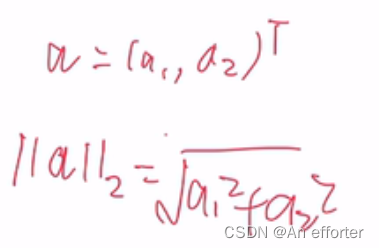
再取个平方，就可以把根号去掉， 就相当于求向量的内积。
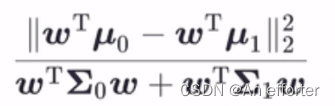
这个公式分母是让同类样例投影点的协方差尽可能小，即分母尽可能小；分子是异类样例的投影点尽可能远离，让类中心之间的距离尽可能大，即分母尽可能大。同时考虑二者，则可得到欲最大化的目标。
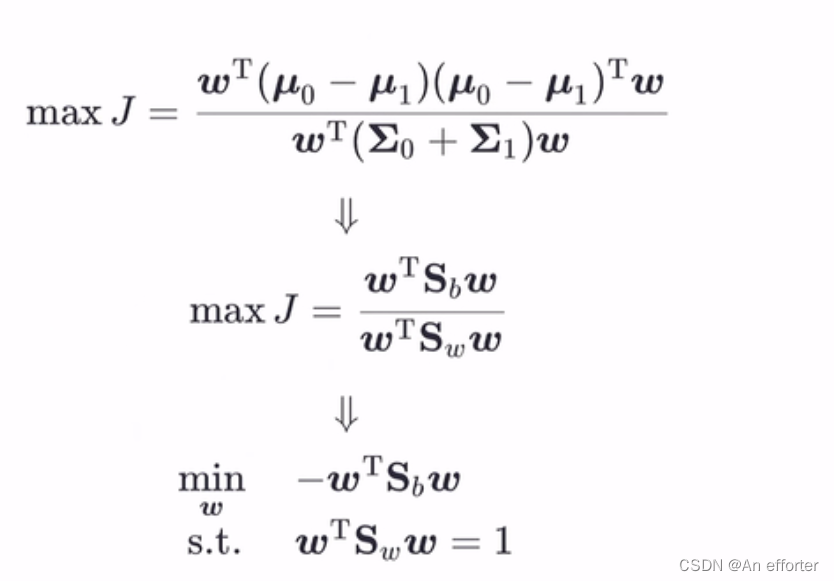
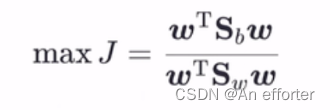这既是LDA欲最大化的目标，即
和
是“广义瑞利商”。
固定分母，等式就好解了，分子加个负号，就成了最小值。
解带约束的式子
，最常用的方法是拉格朗日乘子法。
3.拉格朗日乘子法以及求解过程
知道了原理，进行求解w：
4.补充广义特征值
5.补充广义瑞利商
