机器人学中的状态估计学习笔记(一)第二章 概率论基础
所谓的状态估计问题,本质上是根据系统的先验模型和观测数据,对系统内部状态进行重新估计的问题。
2.1 概率密度函数
2.1.1 定义
定义x为区间[a,b]上的随机变量,服从某个概率密度函数 p ( x ) p(x) p(x),那么该函数 p ( x ) p(x) p(x)必须满足:
∫ a b p ( x ) d x = 1 \int_{a}^{b} p(x)dx=1 ∫abp(x)dx=1 p ( x ) p(x) p(x)函数的积分为1是为了满足全概率公理。
对于条件概率来说,假设p(x|y)表示自变量x ∈ \in ∈[a,b]在条件y ∈ \in ∈[r,s]下的概率函数,那么它满足:
( ∀ y ) ∫ a b p ( x ∣ y ) d x = 1 (\forall y)\int_{a}^{b} p(x|y)dx=1 (∀y)∫abp(x∣y)dx=1 N维连续型随即变量的联合概率密度函数也可以表示 p ( x ) p(x) p(x),其中x=(x1,…,xN)。对于每个xi,满足
xi ∈ \in ∈[ai,bi],那么,实际上也可以用 p ( x 1 , x 2 , . . . , x N ) p(x_{1} ,x_{2} ,...,x_{N} ) p(x1,x2,...,xN)代替 p ( x ) p(x) p(x)。
也可以用 p ( x , y ) p(x,y) p(x,y)来表示x,y的联合密度。
2.1.2 贝叶斯公式及推断
一个联合概率密度可以分解为一个条件概率密度和一个非条件概率密度的乘积:
p ( x , y ) = p ( x ∣ y ) p ( y ) = p ( y ∣ x ) p ( x ) p(x,y)=p(x|y)p(y)=p(y|x)p(x) p(x,y)=p(x∣y)p(y)=p(y∣x)p(x)由上式可得贝叶斯公式:
p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) p(x|y)=\frac{p(y|x)p(x)}{p(y)} p(x∣y)=p(y)p(y∣x)p(x)由于 p ( y ) = p ( y ) ∫ p ( x ∣ y ) d x ⏟ 1 = ∫ p ( x ∣ y ) p ( y ) d x = ∫ p ( x , y ) d x = ∫ p ( y ∣ x ) p ( x ) d x p(y)=p(y)\underset{1}{\underbrace{\int p(x|y)dx} } =\int p(x|y)p(y)dx=\int p(x,y)dx=\int p(y|x)p(x)dx p(y)=p(y)1
∫p(x∣y)dx=∫p(x∣y)p(y)dx=∫p(x,y)dx=∫p(y∣x)p(x)dx所以 p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) = p ( y ∣ x ) p ( x ) ∫ p ( y ∣ x ) p ( x ) d x p(x|y)=\frac{p(y|x)p(x)}{p(y)}= \frac{p(y|x)p(x)}{\int p(y|x)p(x)dx} p(x∣y)=p(y)p(y∣x)p(x)=∫p(y∣x)p(x)dxp(y∣x)p(x) 因此,如果已知状态的先验概率密度函数 p ( x ) p(x) p(x)和传感器模型 p ( y ∣ x ) p(y|x) p(y∣x),就可以推断出状态的后验概率密度函数 p ( x ∣ y ) p(x|y) p(x∣y)。
2.1.3 矩
概率密度的0阶矩为整个全事件的概率,恒等于1。
概率一阶矩称为期望,用 μ μ μ表示:
μ = E [ x ] = ∫ x p ( x ) d x \mu =E[x]=\int xp(x)dx μ=E[x]=∫xp(x)dx对于一般的矩阵函数F(x),为:
E [ F ( x ) ] = ∫ F ( x ) p ( x ) d x E[F(x)]=\int F(x)p(x)dx E[F(x)]=∫F(x)p(x)dx展开形式为:
E [ F ( x ) ] = E [ f i j ( x ) ] = ∫ f i j p ( x ) d x E[F(x)]=E[f_{ij} (x)]=\int f_{ij}p(x)dx E[F(x)]=E[fij(x)]=∫fijp(x)dx 概率二阶矩称为协方差矩阵 Σ \Sigma Σ :
Σ = E [ ( x − μ ) ( x − μ ) T ] \Sigma =E[(x-\mu )(x-\mu)^{T} ] Σ=E[(x−μ)(x−μ)T]三阶和四阶矩分别叫做偏度和峰度。
2.1.5 统计独立性和不相关性
如果两个随机变量x和y的联合概率密度函数可以按下式进行因式分解,那么这个两个随机 变量是统计独立的:
p ( x , y ) = p ( x ) p ( y ) p(x,y)=p(x)p(y) p(x,y)=p(x)p(y)同样地,如果这两个变量的期望运算满足下式,则它们是不相关的:
E [ x y T ] = E [ x ] E [ y ] T E[xy^{T} ]=E[x]E[y]^{T} E[xyT]=E[x]E[y]T但是“不相关"比”独立“更弱。如果两个随机变量是统计独立的,那么它们一定不相关,但是如果两个随机变量是不相关的,那么它们不一定是统计独立的。
2.1.6 归一化积
如果p1(x)和p2(x)是随机变量x的两个不同的概率密度函数,那么它们的归一化积定义为:
p ( x ) = η p 1 ( x ) p 2 ( x ) p(x)=\eta p_{1} (x)p_{2} (x) p(x)=ηp1(x)p2(x)其中 η = ( ∫ p 1 ( x ) p 2 ( x ) d x ) − 1 \eta=\left ( \int p_{1} (x)p_{2} (x)dx \right ) ^{-1} η=(∫p1(x)p2(x)dx)−1是一个常值的归一化因子,用于确保p(x)满足全概率公理。
2.2 高斯概率密度函数
2.2.1 定义
在一维情况下,高斯概率密度函数表示为:
p ( x ∣ μ , σ 2 ) = 1 2 π σ 2 e x p ( − 1 2 ( x − μ ) 2 σ 2 ) p(x|\mu ,\sigma^{2} )=\frac{1}{\sqrt{2\pi \sigma^{2}} }exp\left ( -\frac{1}{2}\frac{(x-\mu )^{2} }{\sigma^{2}} \right ) p(x∣μ,σ2)=2πσ21exp(−21σ2(x−μ)2)其一维高斯PDF的图像如下:

多维变量的高斯分布表示为:
p ( x ∣ μ , Σ ) = 1 ( 2 π ) N d e t Σ e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x|\mu ,\Sigma )=\frac{1}{\sqrt{ (2\pi)^N det\Sigma} }exp\left ( -\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1} (x-\mu ) \right ) p(x∣μ,Σ)=(2π)NdetΣ1exp(−21(x−μ)TΣ−1(x−μ))其中 μ = E [ x ] = ∫ − ∞ ∞ x 1 ( 2 π ) N d e t Σ e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) d x \mu=E[x]=\int_{-\infty }^{\infty } x\frac{1}{\sqrt{ (2\pi)^N det\Sigma} }exp\left ( -\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1} (x-\mu ) \right )dx μ=E[x]=∫−∞∞x(2π)NdetΣ1exp(−21(x−μ)TΣ−1(x−μ))dx Σ = E [ ( x − μ ) ( x − μ ) T ] = ∫ − ∞ ∞ ( x − μ ) ( x − μ ) T 1 ( 2 π ) N d e t Σ e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) d x \Sigma =E[(x-\mu )(x-\mu )^{T} ]=\int_{-\infty }^{\infty } (x-\mu )(x-\mu )^{T}\frac{1}{\sqrt{ (2\pi)^N det\Sigma} }exp\left ( -\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1} (x-\mu ) \right )dx Σ=E[(x−μ)(x−μ)T]=∫−∞∞(x−μ)(x−μ)T(2π)NdetΣ1exp(−21(x−μ)TΣ−1(x−μ))dx习惯上,将正态分布(高斯分布)记为:
x ∼ N ( μ , Σ ) x\sim N(\mu ,\Sigma ) x∼N(μ,Σ)如果随机变量x满足: x ∼ N ( 0 , 1 ) x\sim N(0 ,1 ) x∼N(0,1)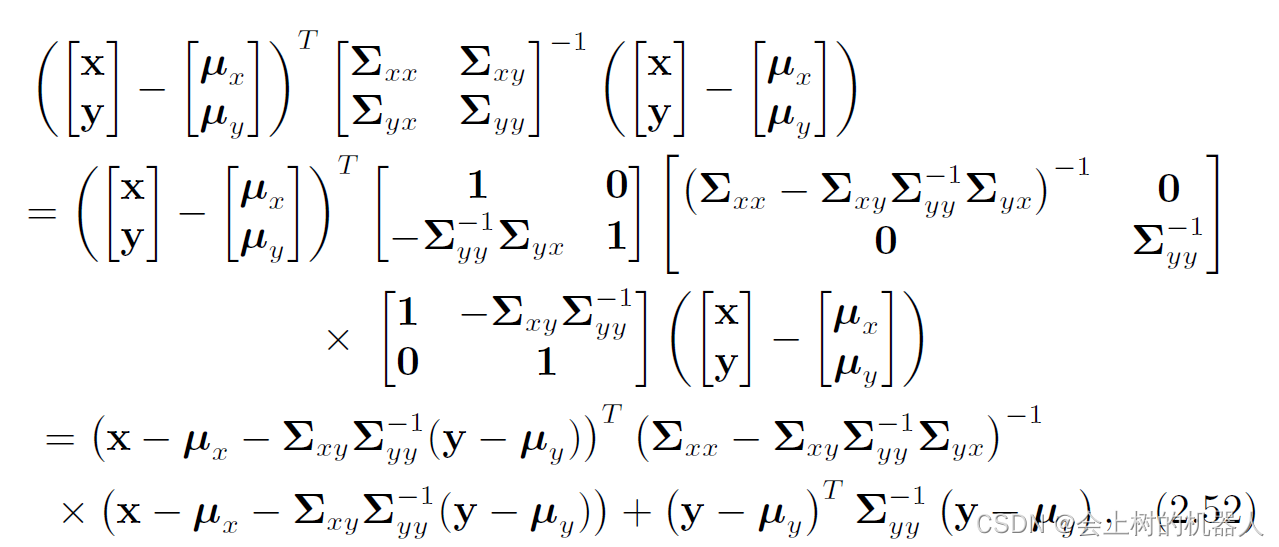
其中1是一个N×N的单位矩阵,可以认为随机变量x服从标准正态分布。
2.2.3 联合高斯概率密度函数,分解与推断
设一对变量(x,y)服从多元正态分布,它们的联合概率密度函数为:
p ( x , y ) = N ( [ μ x μ y ] , [ Σ x x Σ x y Σ y x Σ y y ] ) p(x,y)=N\left ( \begin{bmatrix} \mu _{x} \\\mu _{y} \end{bmatrix} ,\begin{bmatrix} \Sigma _{xx} & \Sigma _{xy}\\ \Sigma _{yx} &\Sigma _{yy} \end{bmatrix}\right ) p(x,y)=N([μxμy],[ΣxxΣyxΣxyΣyy]) 联合概率密度函数p(x,y)指数部分的二次项化简如下:
首先用舒尔补对其协方差矩阵进行分解:
[ Σ x x Σ x y Σ y x Σ y y ] = [ 1 Σ x y Σ y y − 1 0 1 ] [ Σ x x − Σ x y Σ y y − 1 Σ y x 0 0 Σ y y ] [ 1 0 Σ y y − 1 Σ y x 1 ] \begin{bmatrix} \Sigma _{xx} &\Sigma _{xy} \\ \Sigma _{yx} &\Sigma _{yy} \end{bmatrix} =\begin{bmatrix} 1 & \Sigma _{xy}\Sigma _{yy}^{-1} \\ 0 &1 \end{bmatrix} \begin{bmatrix} \Sigma _{xx}-\Sigma _{xy}\Sigma _{yy}^{-1}\Sigma _{yx} & 0 \\ 0 &\Sigma _{yy} \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \Sigma _{yy}^{-1}\Sigma _{yx} &1 \end{bmatrix} [ΣxxΣyxΣxyΣyy]=[10ΣxyΣyy−11][Σxx−ΣxyΣyy−1Σyx00Σyy][1Σyy−1Σyx01]其中1为单位矩阵。再对其进行求逆可得:
[ Σ x x Σ x y Σ y x Σ y y ] − 1 = [ 1 0 − Σ y y − 1 Σ y x 1 ] [ ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 0 0 Σ y y − 1 ] [ 1 − Σ x y Σ y y − 1 0 1 ] \begin{bmatrix} \Sigma _{xx} &\Sigma _{xy} \\ \Sigma _{yx} &\Sigma _{yy} \end{bmatrix}^{-1} =\begin{bmatrix} 1 & 0 \\ -\Sigma _{yy}^{-1}\Sigma _{yx} &1 \end{bmatrix} \begin{bmatrix} \left ( \Sigma _{xx}-\Sigma _{xy}\Sigma _{yy}^{-1}\Sigma _{yx} \right ) ^{-1} & 0 \\ 0 &\Sigma _{yy}^{-1} \end{bmatrix} \begin{bmatrix} 1 & -\Sigma _{xy}\Sigma _{yy}^{-1} \\ 0 &1 \end{bmatrix} [ΣxxΣyxΣxyΣyy]−1=[1−Σyy−1Σyx01][(Σxx−ΣxyΣyy−1Σyx)−100Σyy−1][10−ΣxyΣyy−11]因此,可得:
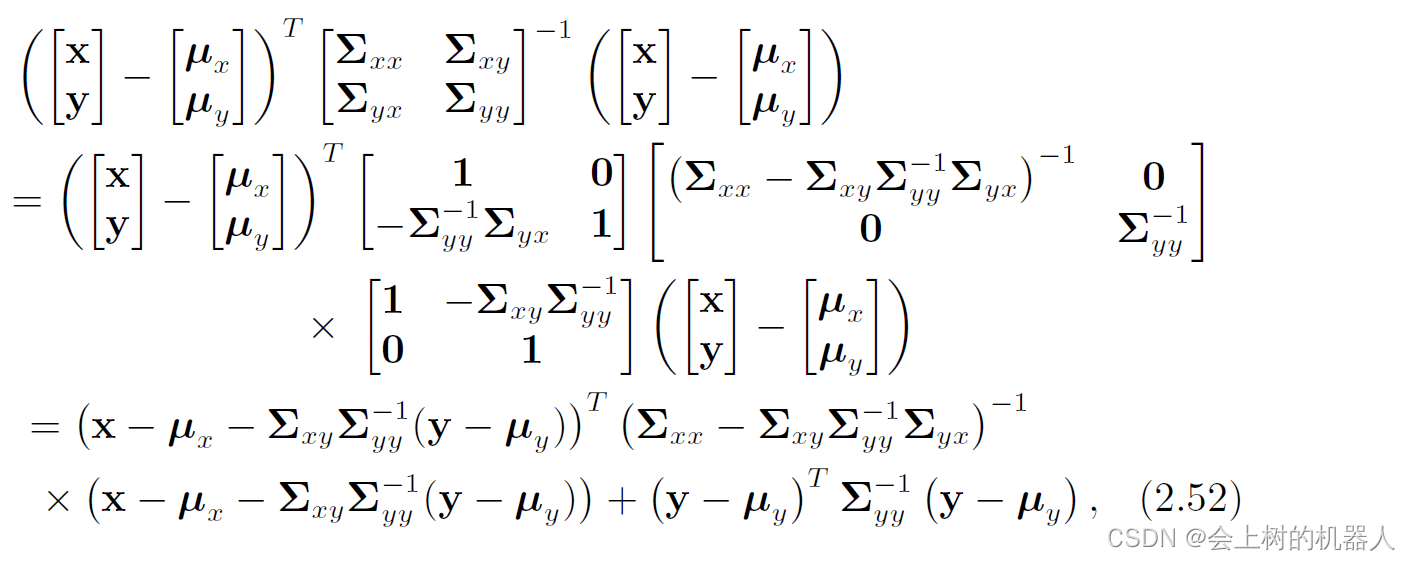
仔细观察上式可以知道,化简后的结果是两个二次项的和,可以分别记为:
x ∼ N ( μ x + Σ x y Σ y y − 1 ( y − μ y ) , Σ x x − Σ x y Σ y y − 1 Σ y x ) x\sim N(\mu _{x} +\Sigma _{xy}\Sigma _{yy}^{-1} (y-\mu _{y}),\Sigma _{xx}-\Sigma _{xy}\Sigma _{yy}^{-1} \Sigma _{yx}) x∼N(μx+ΣxyΣyy−1(y−μy),Σxx−ΣxyΣyy−1Σyx) y ∼ N ( μ y , Σ y y ) y\sim N(\mu _{y},\Sigma _{yy} ) y∼N(μy,Σyy) 因此,可以得到:
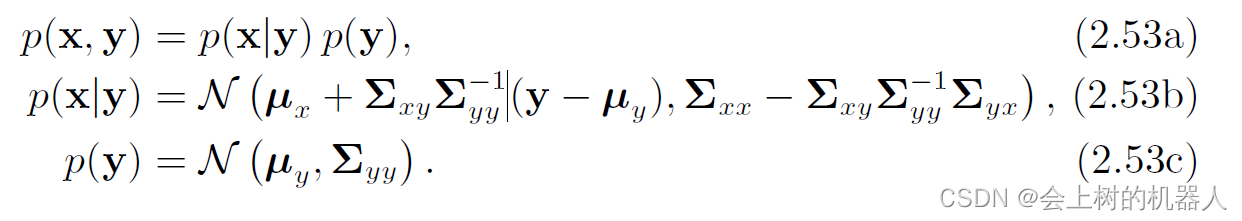
因子p(x|y),p(y)都是高斯概率密度函数,所有如果已知观测值y,就可以通过式(2.53b)通过计算p(x|y)得到在给定y值情况下的x的似然值。
实际上这就是高斯推断中最重要的部分:根据已知状态的先验概率分布,结合观测模型来缩小范围,进一步得到后验概率分布。在式(2.53b)中,可以看到均值发生了一些调整,协方差矩阵也变小了一些,也就是说它的不确定度减小了。
2.2.4 统计独立性、不相关性
在高斯概率密度函数的情况下,统计独立性和不相关性是等价的,即统计独立的两个高斯变量是不相关的(对于一般的概率密度函数通常成立),不相关的两个高斯变量也是统计独立的(并不是所有的概率密度函数都成立)。
2.2.5 高斯分布随机变量的线性变换
假设有高斯随机变量 x ∈ R N ∼ N ( μ x , Σ x x ) x\in \mathbb{R} ^{N} \sim N(\mu _{x },\Sigma _{xx} ) x∈RN∼N(μx,Σxx)以及另一个与x线性相关的随机变量y: y = G x y=Gx y=Gx分别计算其期望和方差:
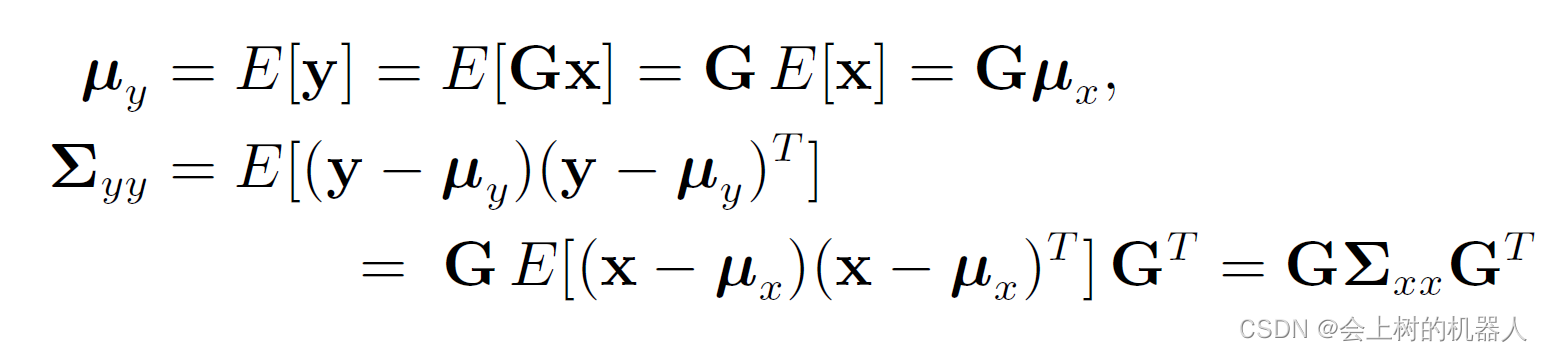
可以得到 y ∼ N ( μ y , Σ y y ) = N ( G μ x , G Σ y y G T ) y \sim N(\mu _{y},\Sigma _{yy} )=N(G\mu _{x},G\Sigma _{yy}G^{T} ) y∼N(μy,Σyy)=N(Gμx,GΣyyGT)。
另一个方法为变量代换法。假设这个映射是单射,即两个x值不可能和同一个y值对应;事实上,可以通过一个更加严格的条件来简化这个单射条件,即G是可逆的(因此M=N)。
根据全概率公理: ∫ a b p ( x ) d x = 1 \int_{a}^{b} p(x)dx=1 ∫abp(x)dx=1一个小区域内的x映射到y上,变为: d y = ∣ d e t G ∣ d x dy=|det G|dx dy=∣detG∣dx于是可以代入上式,可得:
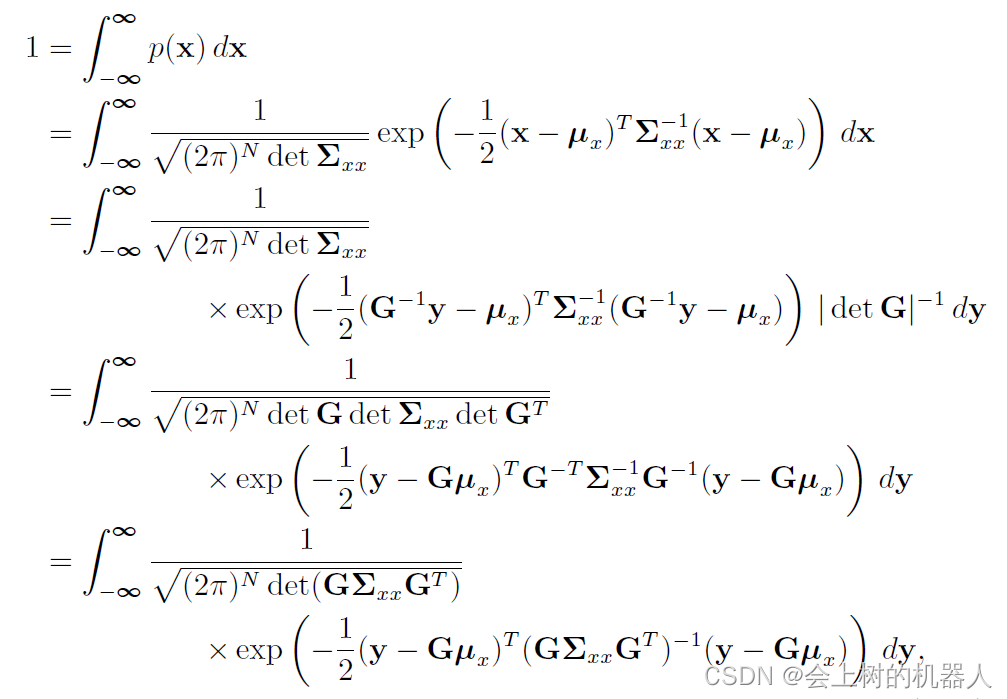
从上式中同样可以得到 μ y = G μ x \mu _{y} =G\mu _{x} μy=Gμx以及 Σ y y = G Σ x x G T \Sigma _{yy} =G\Sigma _{xx}G^{T} Σyy=GΣxxGT。
但是,如果M<N,线性映射就不是单射的了,就无法通过定积分变量代换的方法来求y的分布。不过,如果M<N,rank(G)=M,同样可以考虑从y到x的线性映射。但这会有点麻烦,因为该映射会把变量扩张到一个更大的空间当中,因此实际上得到的x的协方差矩阵会变大。为了避免这个问题,采用信息矩阵的形式,所谓信息矩阵为协方差矩阵的逆,用来表示本次测量的可靠性,即不确定性越小,可靠性越大。令 u = Σ y y − 1 y u=\Sigma _{yy} ^{-1} y u=Σyy−1y可以的得到 u ∼ N ( Σ y y − 1 μ y , Σ y y − 1 ) u\sim N(\Sigma _{yy} ^{-1} \mu _{y},\Sigma _{yy} ^{-1} ) u∼N(Σyy−1μy,Σyy−1)同样地,令 v = Σ x x − 1 x v=\Sigma _{xx} ^{-1} x v=Σxx−1x可以得到 u ∼ N ( Σ x x − 1 μ y , Σ x x − 1 ) u\sim N(\Sigma _{xx} ^{-1} \mu _{y},\Sigma _{xx} ^{-1} ) u∼N(Σxx−1μy,Σxx−1)由于y到x的映射不是唯一的,所以需要选择一个特别的映射,设为: v = G T u ⇔ Σ x x − 1 x = G T Σ y y − 1 y v=G^{T} u\Leftrightarrow \Sigma _{xx}^{-1} x=G^{T} \Sigma _{yy}^{-1} y v=GTu⇔Σxx−1x=GTΣyy−1y那么就可以计算期望:
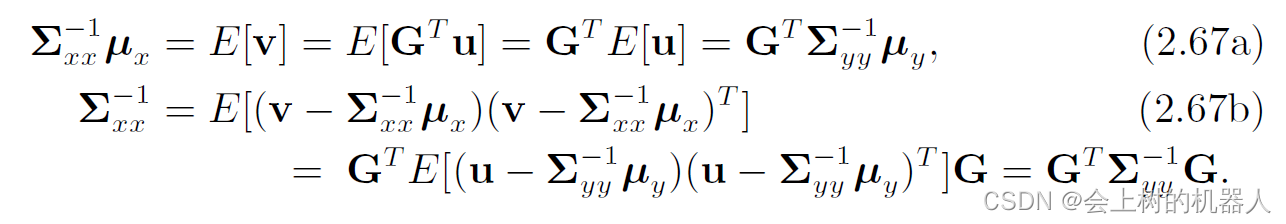
值得注意的是,如果 Σ x x − 1 \Sigma _{xx}^{-1} Σxx−1没有满秩,那就不能恢复 Σ x x \Sigma _{xx} Σxx和 μ x \mu _{x} μx,因而只能以信息的形式表达分布。但是这个信息形式表达的分布也能够融合起来。
2.2.6 高斯概率密度函数的归一化积
高斯概率密度函数中有一个有用的性质,即K个高斯概率密度函数的归一化积仍然是高斯概率密度函数:
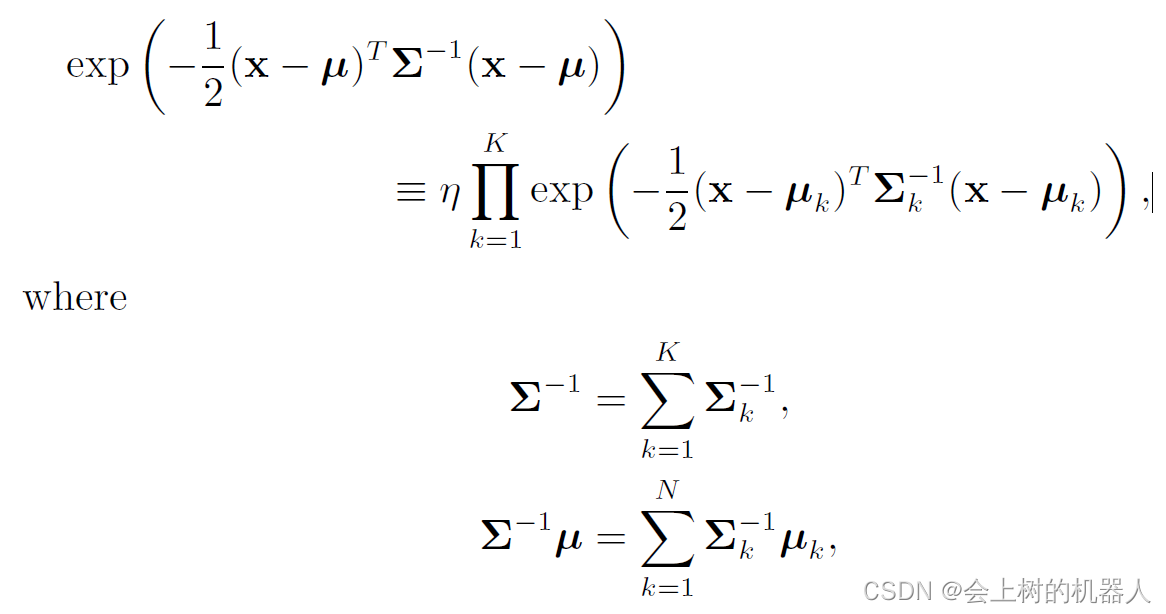
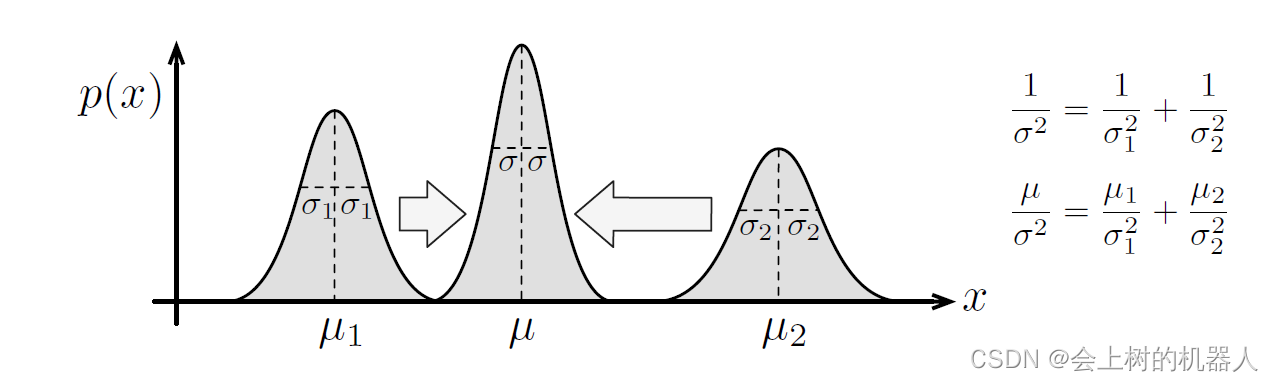
η \eta η是一个归一化常量,它确保密度函数满足全概率公理。当把多个估计融合在一起的时候,就需要用到高斯归一化乘积,如下图所示:
对于高斯分布随机变量的线性变换,我们也有类似的结果:
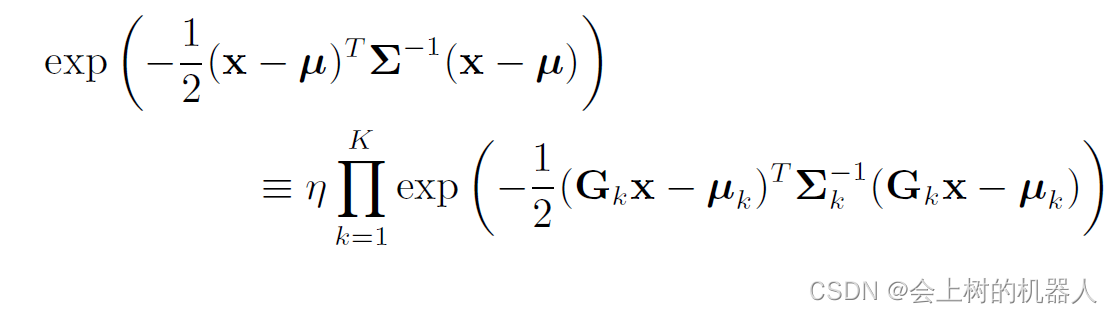
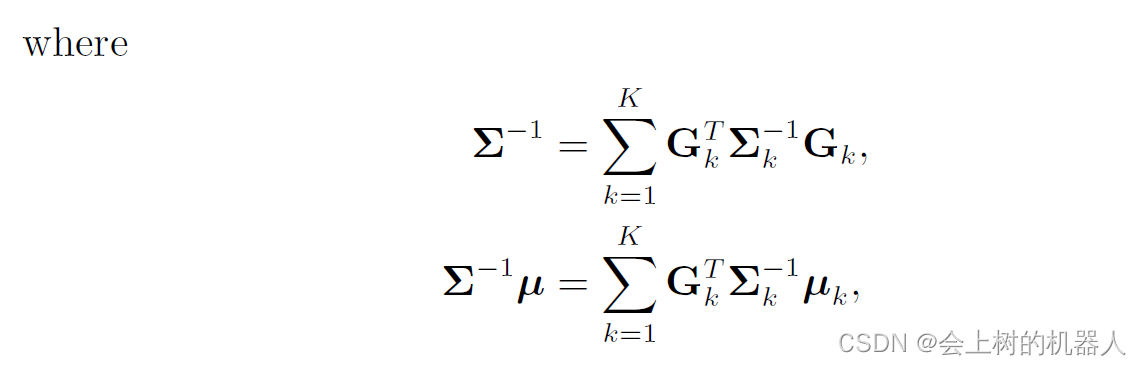
2.2.7 Sherman-Morrison-Woodbury等式
Sherman-Morrison-Woodbury(SMW)恒等式也称为矩阵求逆引理。
对于可逆矩阵,它可以分解为一个下三角-对角-上三角(LDU)形式或上三角-对角-下三角(UDL)形式,如下所示:
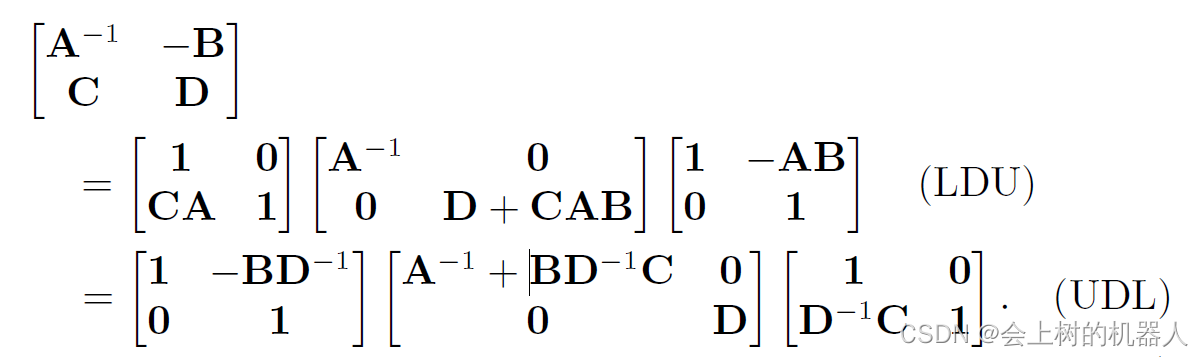
然后对等式两侧求逆。对于LDU,可得:
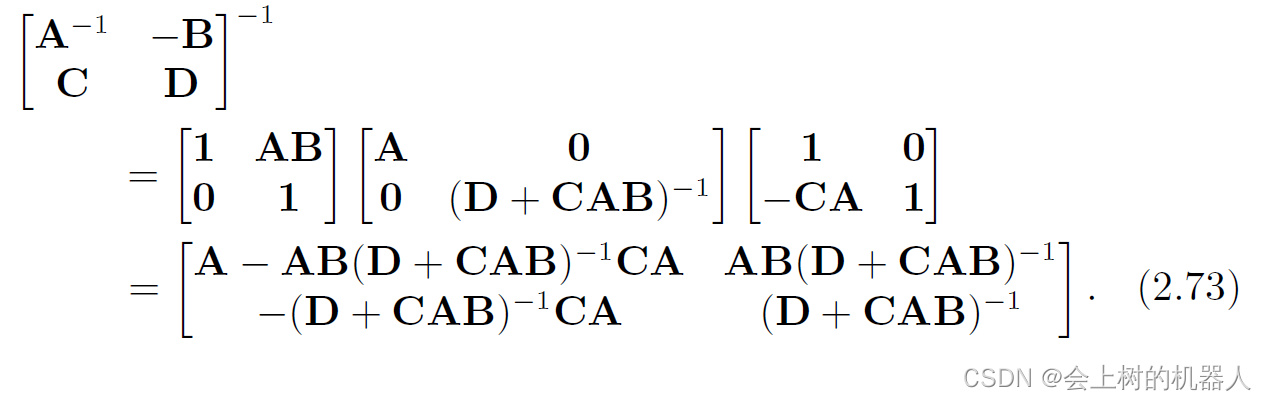
对于UDL,可得:
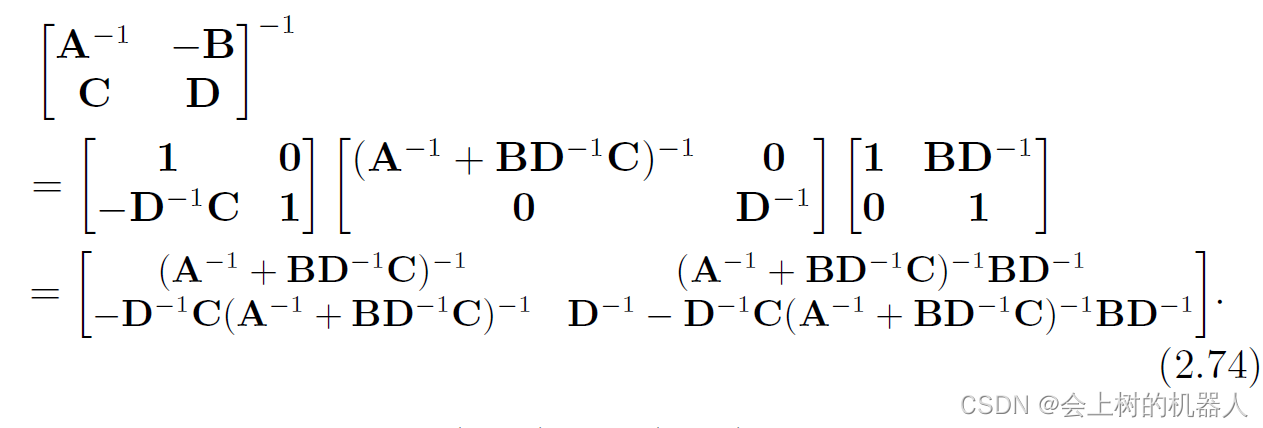 对比式(2.73)和式(2.74)的结果,可以得到如下等式:
对比式(2.73)和式(2.74)的结果,可以得到如下等式:
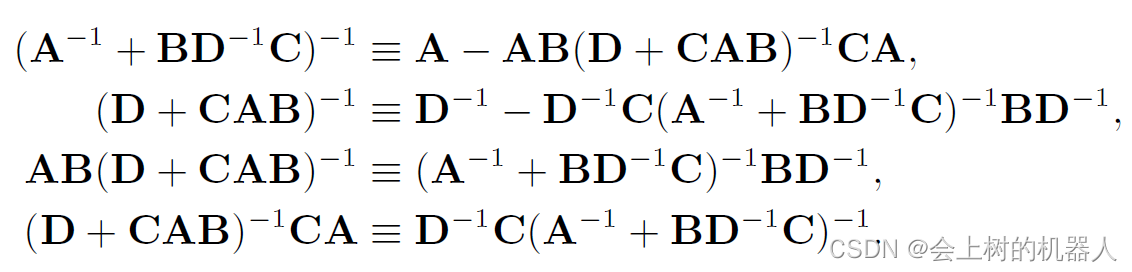
在后面处理高斯概率密度函数的协方差矩阵时,将频繁地用到这些恒等式。
2.2.8 高斯分布随机变量的非线性变换
接下来研究高斯分布经过一个随机非线性变换之后的情况,即计算: p ( y ) = ∫ − ∞ ∞ p ( y ∣ x ) p ( x ) d x p(y)=\int_{-\infty }^{\infty } p(y|x)p(x)dx p(y)=∫−∞∞p(y∣x)p(x)dx其中 p ( y ) = ∫ − ∞ ∞ p ( y ∣ x ) p ( x ) d x p(y)=\int_{-\infty }^{\infty } p(y|x)p(x)dx p(y)=∫−∞∞p(y∣x)p(x)dx p ( x ) = N ( μ x , Σ x x ) p(x)=N(\mu _{x} ,\Sigma _{xx} ) p(x)=N(μx,Σxx)这里g(·)表示 g : x ↦ y g:x\mapsto y g:x↦y,是一个非线性映射。它受高斯噪声影响,其协方差为R。后文需要用到这类随机非线性映射对传感器进行建模。将高斯分布传递进非线性变换中是有必要的,例如,再贝叶斯推断时,贝叶斯公式的分母往往就存在这样的一个非线性变换。
标量情况下的非线性映射
首先看一下简化的情况:x为标量,非线性函数g(·)是确定的(即R=0)。设 x ∈ R 1 x\in \mathbb{R} ^{1} x∈R1为高斯随机变量: x ∼ N ( 0 , σ 2 ) x\sim N(0,\sigma ^{2} ) x∼N(0,σ2)x的PDF为: P ( x ) = 1 2 π σ 2 e x p ( − 1 2 x 2 σ 2 ) P(x)=\frac{1}{\sqrt{2\pi \sigma^{2} } } exp(-\frac{1}{2} \frac{x^{2} }{\sigma^{2}} ) P(x)=2πσ21exp(−21σ2x2)现在考虑非线性映射: y = e x p ( x ) y=exp(x) y=exp(x)它显然是可逆的: x = l n ( y ) x=ln(y) x=ln(y)在无穷小区间上,x和y的关系为: d y = e x p ( x ) d x dy=exp(x)dx dy=exp(x)dx或者 d x = 1 y d y dx=\frac{1}{y} dy dx=y1dy根据全概率公理,有:
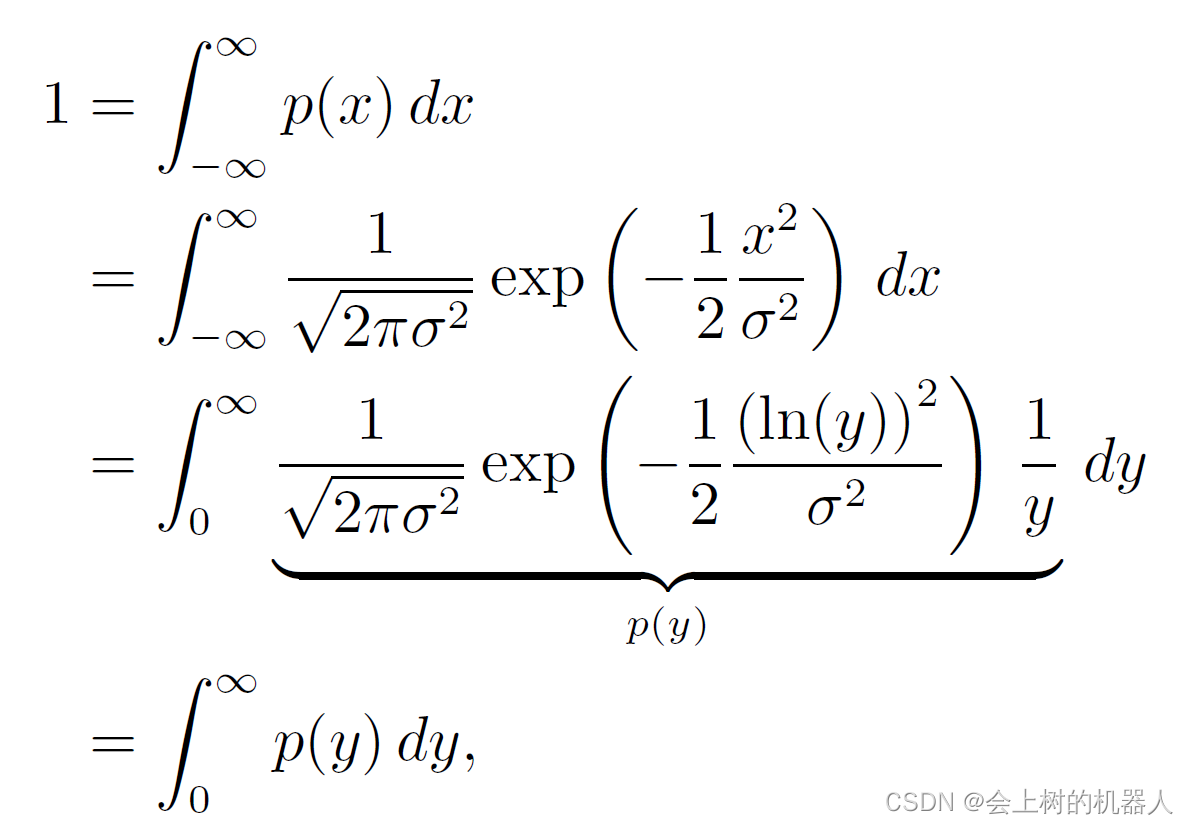
上式为p(y)的确切表达式,当 σ 2 = 1 \sigma ^2=1 σ2=1时,它的图像如下图所示:
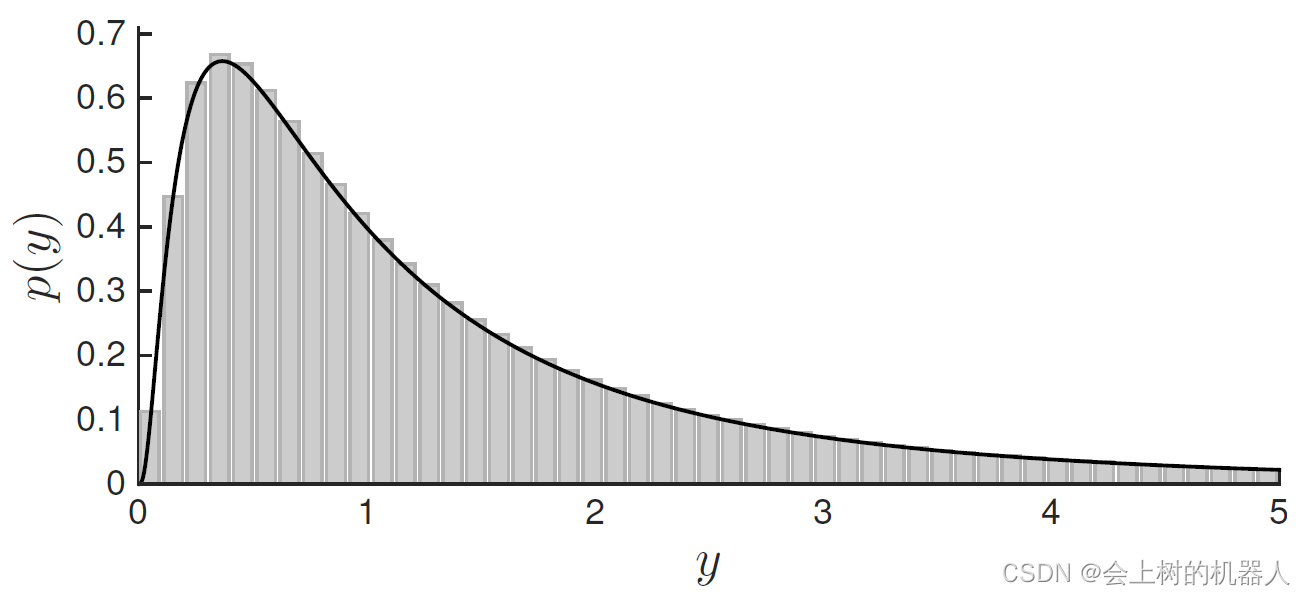
曲线以下的部分从y=0到 ∞ \infty ∞的面积总和为1.通过对x进行大量采样,再经过非线性变换g(·)后,可以得到灰色的直方图,它可以看作是黑色曲线的近似值。可以看到该近似值吻合于真实值,验证了上述变换的正确性。
注意,因为经过了非线性变换,p(y)不再服从高斯分布。
一般情况下的线性化处理
然而并不是对于每一个g(·)都能得到闭式解,而且在多维变量的情况下,计算会变得无比复杂。另外,当非线性变换具有随机性时(R>0),由于存在多余的噪声输入,映射必然是不可逆的,因此需要采用不同的方法来解决这种情况。处理的方法有很多种,本次将介绍最常用的方法,线性化。
对非线性变换进行线性化后,得到: g ( x ) ≈ μ y + G ( x − μ x ) g(x)\approx \mu _{y} +G(x-\mu _{x} ) g(x)≈μy+G(x−μx) G = ∂ g ( x ) ∂ x ∣ x = μ x G=\frac{\partial g(x)}{\partial x} \mid_{ x=\mu _{x} } G=∂x∂g(x)∣x=μx μ y = g ( μ x ) \mu _{y}=g(\mu _{x}) μy=g(μx)其中G是g(·)关于x的雅可比矩阵。在线性化后,就可以得到上述问题的“闭式解”,这个解实际上是上述问题的一个近似解,当这个映射的非线性性质不强的时候,该近似解才成立。
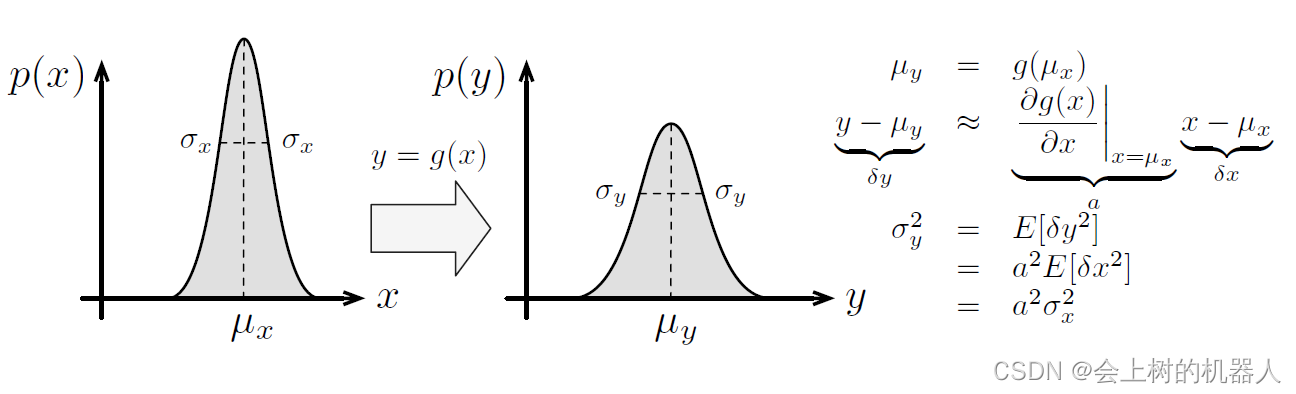 如上图所示,描述了一个一维高斯PDF通过非线性变换g(·)后的结果,其中对g(·)进行了线性化。
如上图所示,描述了一个一维高斯PDF通过非线性变换g(·)后的结果,其中对g(·)进行了线性化。
由该式: p ( y ) = ∫ − ∞ ∞ p ( y ∣ x ) p ( x ) d x p(y)=\int_{-\infty }^{\infty } p(y|x)p(x)dx p(y)=∫−∞∞p(y∣x)p(x)dx可得:
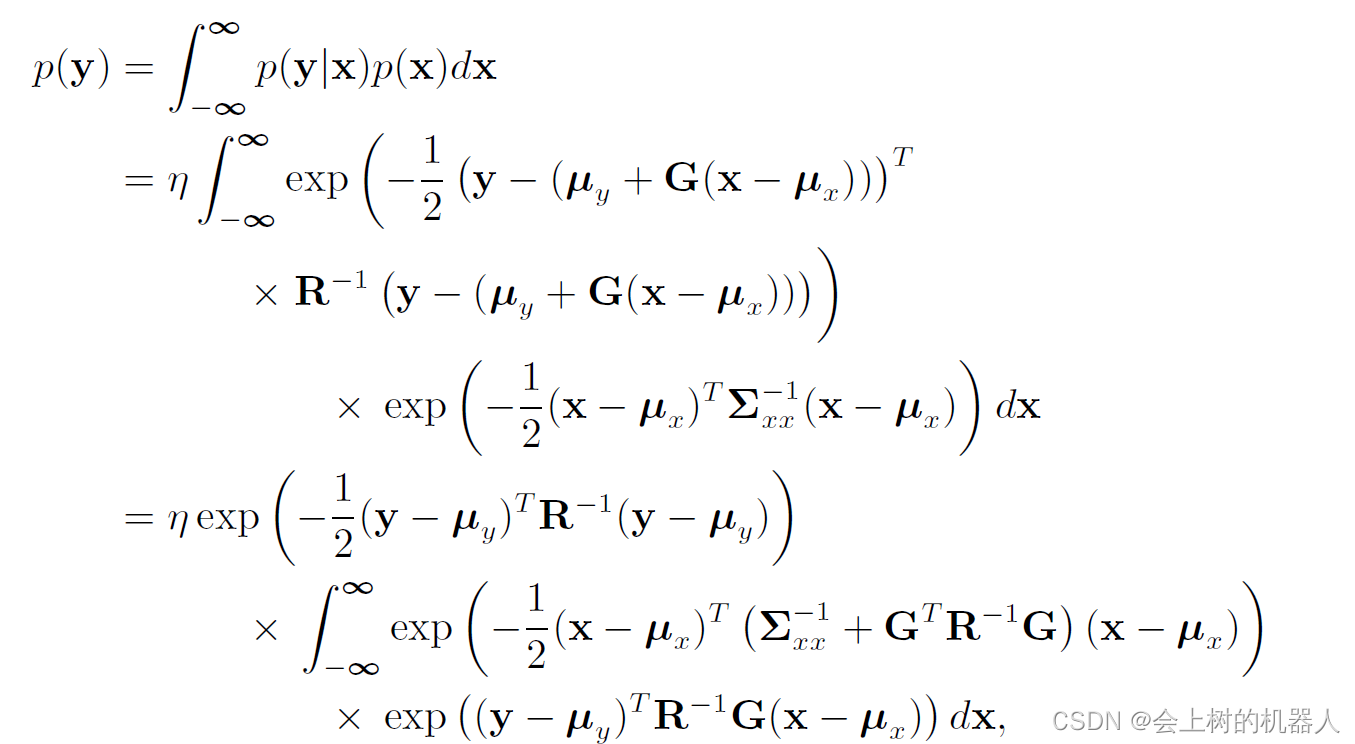
其中 η \eta η是归一化常量,定义矩阵F,使得: F T ( G T R − 1 G + Σ x x − 1 ) = R − 1 G F^{T} (G^{T} R^{-1} G+\Sigma _{xx} ^{-1} )=R^{-1} G FT(GTR−1G+Σxx−1)=R−1G于是需要补全积分里的平方项,即:
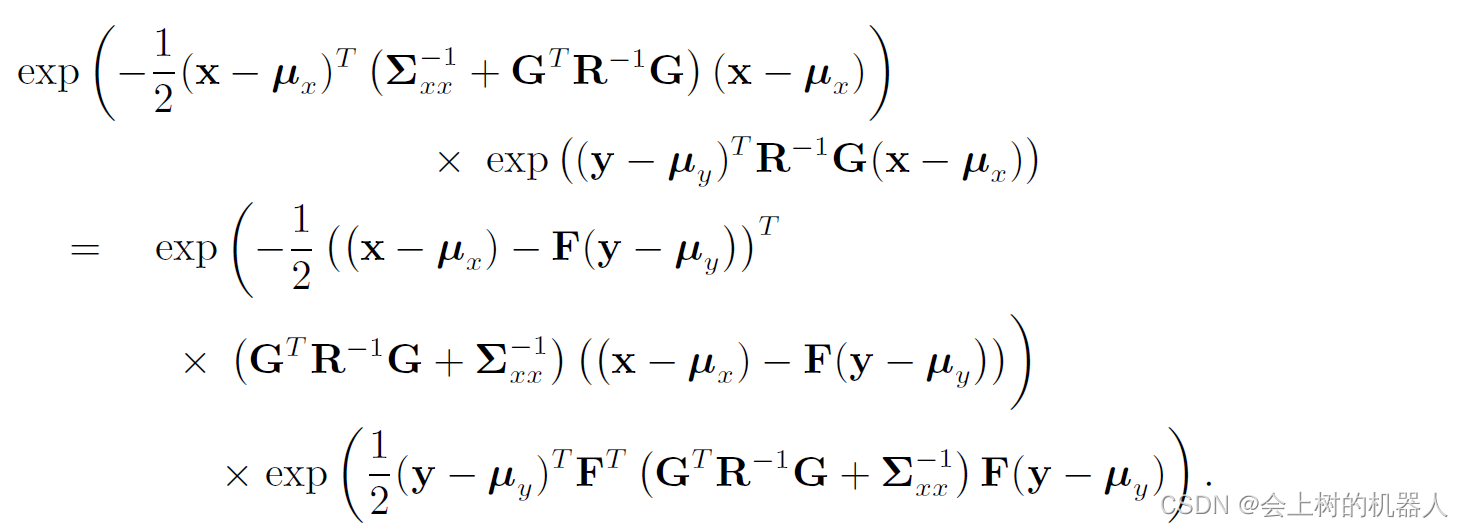
其中第二个因子与x无关,不需要对其进行积分。第一个因子为x的高斯分布,因此对x积分可以得到一个常数,再与常数 η \eta η合并。同样地,对p(y),有:
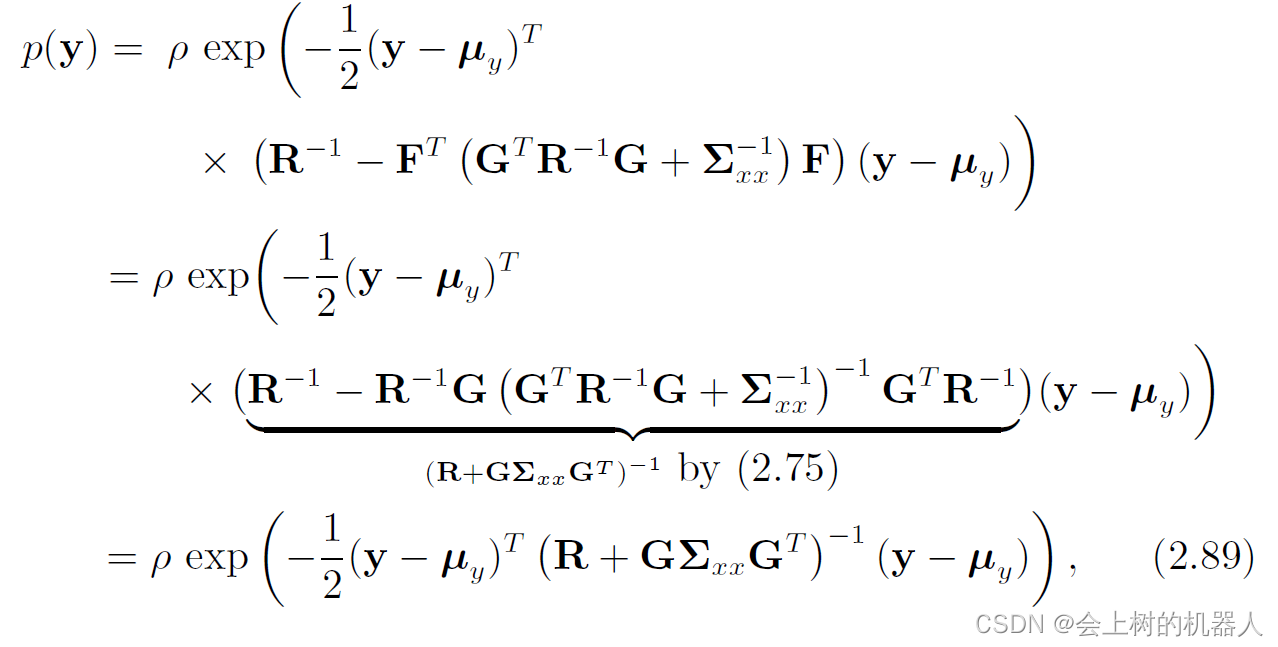
其中 ρ \rho ρ是一个新的归一化常量。该式即y的高斯分布: y ∼ N ( μ y , Σ y y ) = N ( g ( μ x ) , R + G Σ x x G T ) y\sim N(\mu _{y},\Sigma _{yy} )=N(g(\mu _{x} ),R+G\Sigma _{xx} G^{T}) y∼N(μy,Σyy)=N(g(μx),R+GΣxxGT)
2.3 高斯过程
将满足高斯分布的变量 x ∈ R N x\in \mathbb{R} ^{N} x∈RN记为: x ∼ N ( μ , Σ ) x\sim N(\mu ,\Sigma ) x∼N(μ,Σ)并大量使用这类随机变量表达离散时间的状态量。
接着将讨论时间t上的连续的状态量。为此,首先需要引入高斯过程。如下图描述了高斯过程表示的轨迹,其中每个时刻的均值用一个均值函数 σ ( t ) \sigma(t) σ(t)描述,两个不同时刻的方差用一个协方差函数 Σ ( t , t ′ ) \Sigma (t,t') Σ(t,t′)描述。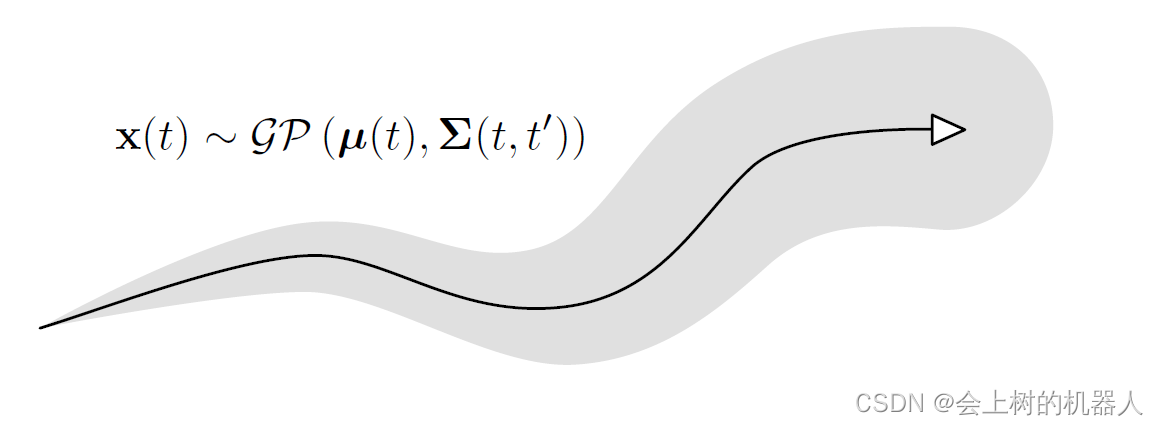
其中黑色的实线为均值函数,阴影区域为协方差函数。
可以认为整个轨迹是一类函数集合中的一个随机变量。一个函数越接近均值函数,轨迹就越相像。协方差函数通过描述两个时刻t,t’的随机变量的相关性来刻画轨迹的平滑程度。我们把这个随机变量函数记为: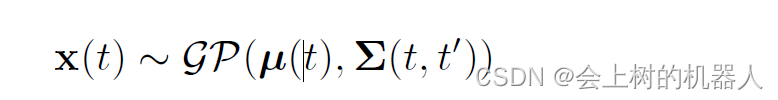 它表明了连续时间轨迹是一个高斯过程。实际上高斯过程不仅限于表达对于时间是一维的情况。
它表明了连续时间轨迹是一个高斯过程。实际上高斯过程不仅限于表达对于时间是一维的情况。
如果只对某个特定时间 τ \tau τ的情况感兴趣,可以写出如下表达式: x ( τ ) ∼ N ( μ ( τ ) , Σ ( τ , τ ) ) x(\tau)\sim N(\mu (\tau ),\Sigma (\tau ,\tau )) x(τ)∼N(μ(τ),Σ(τ,τ))此处 Σ ( τ , τ ) \Sigma (\tau ,\tau ) Σ(τ,τ)就是普通的协方差矩阵。我们可以边缘化所有其他时刻,只留下这个特定时间 τ \tau τ下的 x ( τ ) x(\tau) x(τ),可以把它看作一般的高斯随机变量。
通常高斯过程有不同的表现形式。常用的一个高斯过程是零均值、白噪声的高斯过程。对于零均值白噪声 ω ( τ ) \omega (\tau ) ω(τ),记为: ω ( τ ) ∼ g p ( 0 , Q δ ( t − t ′ ) ) \omega (\tau )\sim \mathcal{g} \mathcal{p} (0,Q\delta (t-t')) ω(τ)∼gp(0,Qδ(t−t′))其中Q是能量谱密度矩阵, δ ( t − t ′ ) \delta (t-t') δ(t−t′)是狄拉克 δ \delta δ 函数。由于它的值只取决于时间差t-t’,因此零均值的白噪声过程实际上是一个平稳噪声过程。
参考资料:
《机器人学中的状态估计》