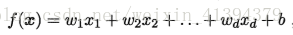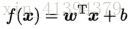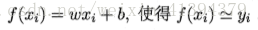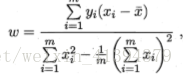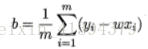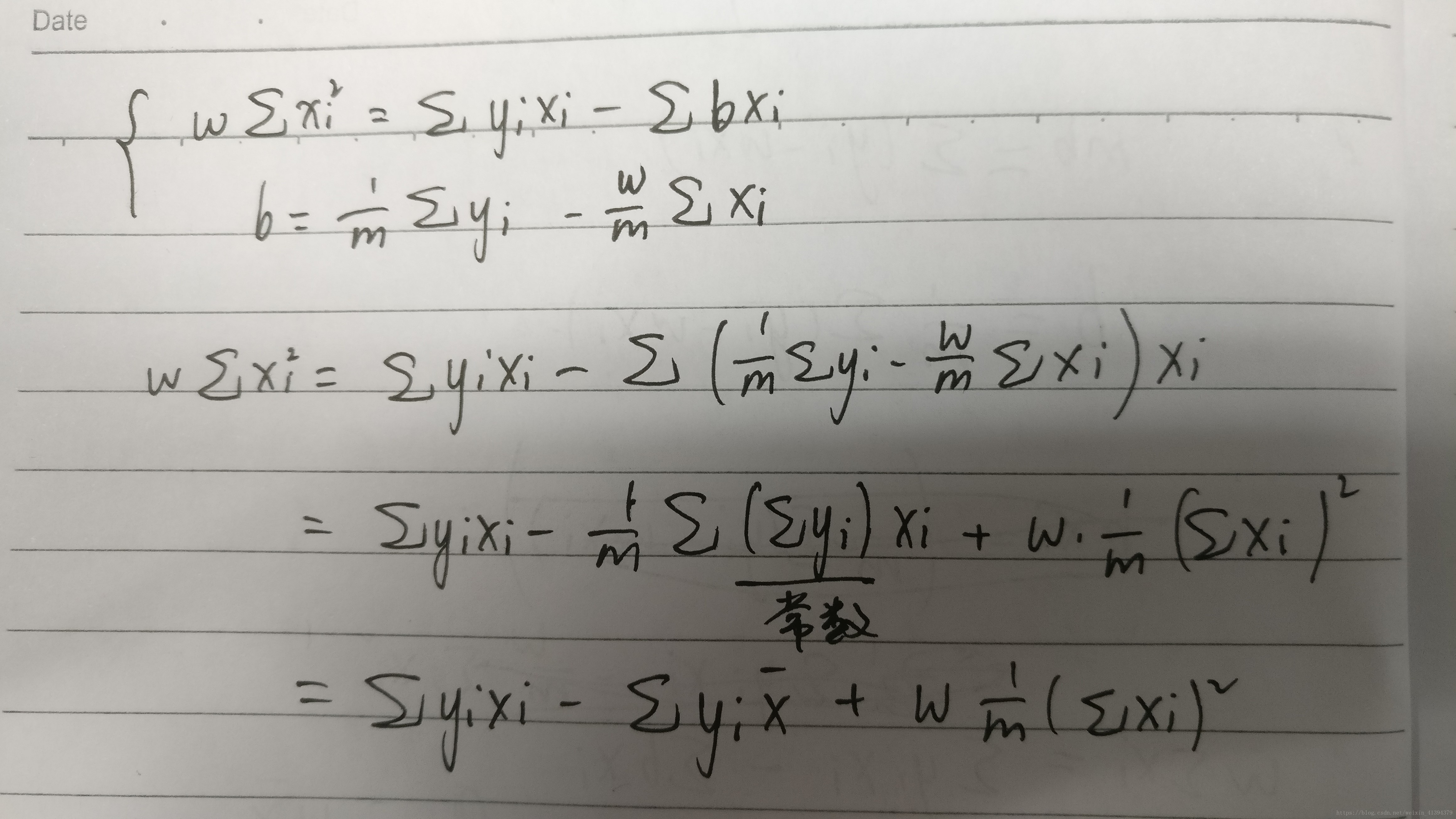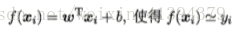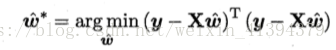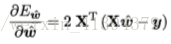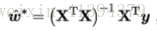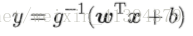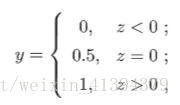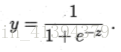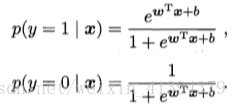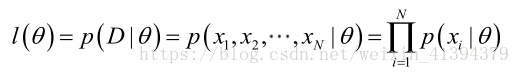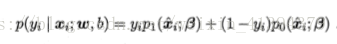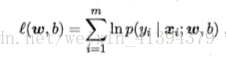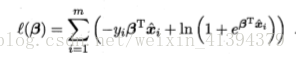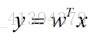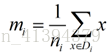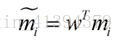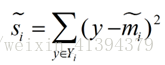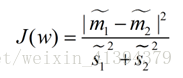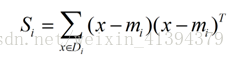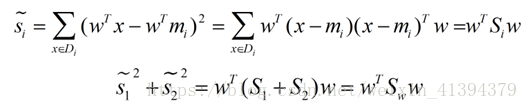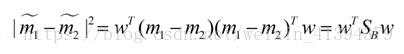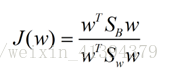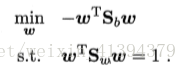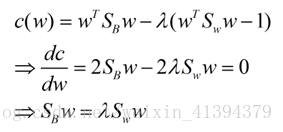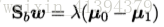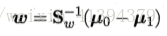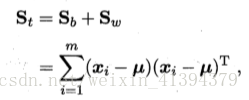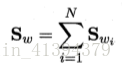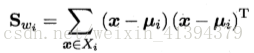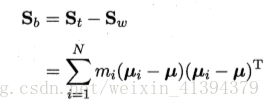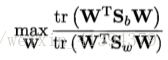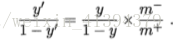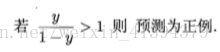机器学习笔记（三） 第三章 线性模型

3.1 基本形式

样本x由d个属性描述 x= (x1; x2;…; xd)， 线性模型试图学得一个通过属性的线性组合来进行预测的函数：

向量形式：

w和b学得之后，模型就得以确定.

3.2 线性回归

线性回归试图学得

为确定w，b，学习到泛化性能最好的模型，因回归问题的性能度量为均方误差，所以我们确定w、b的标准为最小化均方误差（即找到一条拟合直线，是所有样本到这条直线上的欧式距离最小，即拟合效果最好），方法为最小二乘法（由于均方误差E(w,b)为关于w，b的凸函数，极值出现在使w、b导数为零的点）。

求解导数为零的点，得到w，b的最优解的闭式解

推导过程

对于多元线性回归，样本由d个属性描述，我们试图学得模型：

数据集D描述为m×(d+1)大小的矩阵（含有偏置列1,即每个样本多一个属性恒为1），w和b并为一个向量(w;b)，把标记也写成向量形式y=(y1;y2;y3;…;ym):
所以此时均方误差为X(m×2),w^(2×1),y(m×1)
我们需要确定使其最小时的w^:

求导得到

可以根据此式解得w^矩阵，当XTX满秩（可逆）,可得：
然而，现实中往往不是满秩的，此时可解的多个w^，此时一般一如正则化。
广义线性模型，函数g(·)为联系函数（将线性回归模型与其他非线性的真实标记相联系），需要光滑且连续

3.3 对数几率回归

二分类任务（虽然叫回归，但是一种分类学习方法），输出标记y∈{0,1}。而线性回归模型产生的预测值是实值，需将实值z=wTx+b转化为0/1值。
最理想的是单位阶跃函数：

但单位阶跃函数不连续，不能作为联系函数，无法使用广义线性模型求解w，b(非凸函数不能优化)。使用对数几率函数（是一种sigmoid函数）替代阶跃函数，作为g-1(·)：

将z值转化为y，y∈(0,1),将y看做x为正例的可能性，g(y)=ln(y/1-y)即为对真实标记的对数几率预测，不仅预测出类别，且表明了近似概率。
为确定w和b，此时由于假设函数非线性，若直接使用回归问题的均方误差（使用求差的形式 p(y=1 or 0|x)-y），得到的均方误差（代价函数）是非凸的，无法进行优化。
考虑y为类后验概率（p(w|x),除此之外还有几个概念：先验概率p(w)，类条件概率p(x|w)，p(x)=∑p(x|w)p(w)，p(w|x)=p(w)p(x|w)/p(x)），可以得到：

通过极大似然法（给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。）来估计w和b，令每个样本属于其真实标记的概率越大越好。
似然函数 l(θ)=p(D|θ)，可以理解为参数为θ的模型对训练样本预测的结果恰好是数据集D的概率，越大说明拟合程度越好(相当于用求积的形式取代了求差的形式，更上层的意义是因为这是分类问题，而不是回归问题以分类正确概率作为度量，这样得到的函数可以经过对数变化后变为凸函数，可进行优化)：

其中p(xi|θ)（这里用了β，两个地方的图片伤不起。。）：

（这里有两种表示概率的方法，一种如上公式所示，还有一种指数形式 ）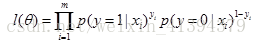
要求得使似然函数最大是参数的取值θ。为便于分析，定义对数似然函数，

最大化上式等价于最小化下式：

再对该函数进行凸优化，这里凸优化只能使用数值优化算法，无解析优化算法，如使用梯度下降法或牛顿法求解，得到迭代形式的解。

3.4 线性判别分析(LDA)

是一种分类方法。线性判别分析又称为Fisher判别分析，是一种最简单的线性分类器。
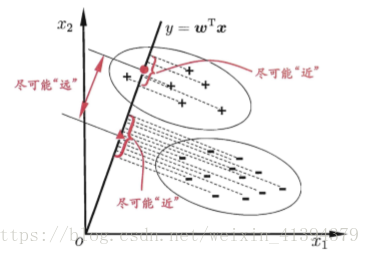
思想：给定一个训练集，将训练集上各样例投影到一条直线上（降维），使相同类别的样例的投影点尽可能近，不同类型的投影点尽可能远。当对新鲜样本进行分类时，也将其向这条直线上投影，再根据投影点位置确定新样本的类别。

假设用来区分二分类的直线（投影函数)为：

LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们需要定义几个关键的值：
类别i的原始中心点为：（Di表示属于类别i的点)

类别i投影后的中心点为：

衡量类别i投影后，类别点之间的分散程度（方差）为：

这里的y=wTx，是每个样本投影后的点，不是样本标签（这里要理解，对一个样本来说(x,y)不是样本坐标，x就表示样本点（坐标），y只是样本属于某一类的一个标签）
最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，越大说明两类越远。我们要使使得类别内的点距离越近越好（集中），类别间的点越远越好，因此需要最大化J(w)，求出最优的w。
下面我们将J(w)中的w提出来：
定义各类内散度矩阵**（协方差矩阵Σ_i：多个变量的方差之和，描述整体误差）：

分母可化为：

定义类间散度矩阵（范数：两点间距离）**：

S_b=(m₁-m₂)(m₁-m₂)^T

分子可化为：

即损失函数：

被称为S_b与S_w的广义瑞利商。LDA的目标即为最大化广义瑞利商。
为确定w，使用拉格朗日乘子法，并且不失一般性的将分母限制为1，只需确定出w的方向，等价于：

使用拉格朗日乘子法：

由于S_bw的方向恒为μ₀-μ₁，有：

即得：


可将LDA推广到多分类任务中
定义全局散度矩阵：

其中 μ 是所有示例的均值向量
类内散度矩阵变为


得到（其中m_i是每类样本的样本数）：

优化目标选用：

W 的闭式解则是 S_w^-1S_b 的 N 一 1 个最大广义特征值所对应的特征向量组成的矩阵.

3.5 多分类学习

多分类学习任务。有些二分类学习方法可直接推广到多分类；而更一般的，我们是基于基本策略，利用二分类学习器解决多分类任务。
考虑N个类别C₁、C₂、…、C_N，基本思路：拆解法，将多分类任务拆解成多个二分类任务。
拆分策略： “一对一” (One vs. One，简称 OvO)、 “一对 其余” (One vs. Rest，简称 OvR)和"多对多" (Many vs. Many，简称 MvM).
OvO:

• 将N个类别两两配对，从而形成C_N²=N(N-1)/2个分类任务,利用选择的两个类训练，最后将新样本同时送给这N(N-1)/2个分类器，把预测的最多的结果作为最终分类结果。
• 存储开销和测试时间开销大，但训练时间开销小

OvR：

• 每次将一类作为正例，剩余的作为反例来训练N个分类器，此时若有一个分类器将测试样本预测为正例，则作为最终预测结果。若有多个分类器预测为正类，选择置信度最大的类别标记作为分类结果。
• 训练时间开销大，存储开销和测试开销小。

MvM:是每次将若干个类作为正类，若干个其他类作为反类。正、反类的构造必须有特殊的设计，不能随意选 取。常用ECOC“纠错输出码”构造。

• 编码：对N个类别进行M次划分，每次将一部分类作为正类，另外作为反类，形成M个二分类训练集，训练出M个分类器
• 解码：M个个分类器对测试样本预测，预测标记组成一个编码，与各个类别各自的编码进行比较，返回其中距离（一般采用欧式距离，海明距离：（编码有几位不同海明距离就是几）不好判断）最小的类别作为预测结果。

编码越长越好，但对有限类别数，码长超过一定范围就失去了意义

扫描二维码关注公众号，回复： 3668456 查看本文章

3.6 类别不平衡

不同类别的训练样本要求数目相当，若差距很大，就是类别不平衡状况。
常遇到，正例较少，反例却多，如OvR,MvM虽然每个类经过多次进行了相同处理，但有时仍不能完全抵消类别不平衡的影响，所以需要了解类别不平衡的处理方法。
再缩放：：满足无偏采样下：训练集中总体类别比例与真实情况下保持一致。


将更改的预测值（带撇的）用下式进行决策。
欠采样：去除一些反例使得正反例数目平衡（随机丢弃反例可能丢失重要信息，采用将反例划分为若干集合供给不同学习器，整体上未丢失重要信息）
过采样：增加一些正例（如采用对当前正例样本插值产生新正例）
阈值移动：将再缩放加入到决策过程