注:本部分博客主要结合周老师的PPT以及查找的资料,尝试去解释Reed-Solomon Codes的数学原理和信息论原理,并讨论Reed-Solomon Codes在QR二维码方面的应用。
Reed-Solomon Codes(RS码),里德·所罗门码,又称纠删码(意思是能容忍丢失的数据),是存储数据时常用的一种可恢复编码,大致原理是将数据设置为n块,RS码将n块数据生成m块校验码,如果数据块与校验码(总共n+m块)中丢失了k块(k<=m)就能通过剩余的数据块与校验块恢复原来的数据块。
这系列将分为“编码原理”与“解码原理”两大块讨论,每块都先解释数学原理,后链接信息论原理,QR二维码将穿插说明。
【编码原理】
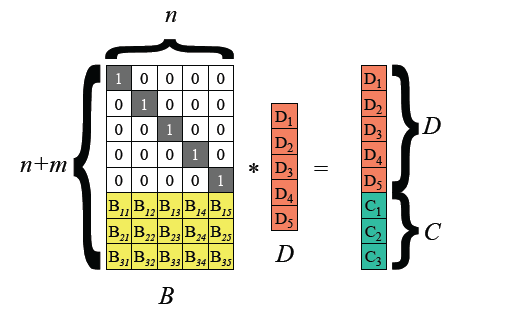
编码过程就是将原始数据变成,以便存储防止丢失的码的过程(对应QR码的格式信息,即掩码+纠错等级)。编码的时候将数据分为字长为w的数据块(QR码一般8 bit为一个word),数据块共有n块,将输入的每个数据作为一个向量存储在矩阵中,设为D=(D1 , D2 .... Dn),编码后也将数据作为向量存储为(D1, D2, D3.....Dn,C1,C2,C3......Cm),即编码后的向量只在原矩阵后缀加了一排向量(C1,C2,C3......Cm),类似图如下:
(图中B中5*5这一块单位矩阵,乘以D矩阵刚好得D矩阵,B中n+1行开始的矩阵乘以D矩阵为C矩阵。)
我们先不讨论为何要将原数据D通过矩阵变换,编码成D+C的具体原因,首先先尝试弄明白其如何用数学模型表达出来以及三个矩阵BCD中里面的内容代表什么。
先结合上图矩阵大致说下数学原理(后面会细说)(周老师的思维太强了,矩阵这一块只有ci几排变量也没有细说,所以。。。我没听懂。。。只能找另外一种方法尝试去理解了。。。):
我们设置m个校验符号,那么就有生成多项式g(x)产生,我们设g(x)=(x-a^0)(x-a^1)·····(x-a^(m-1));设置原输入码D有n个字,设为列表mag_in,则在mag_in后缀加上m个0,若为上图则为mag_in = [d1,d2,d3,d4,d5],变为mag_in=[d1,d2,d3,d4,d5,0,0,0]。然后我们将变化了的mag_in列表变为多项式,通过综合除法(synthetic division),除以生成多项式g(x),得到一个列表为[d1,d2,d3,d4,d5,p1,p2,p3],那么综合除法处理过后的列表d和p代表了什么呢?
其中di对应前面mag_in中的di。如果设g(x)中k个(x-a^任意值)的乘积为mul(k),那么p3就代表了mag_in除以mul(1)的余数,p2就代表了mag_in除以mul(2)的余数,p1就代表了mag_in除以mul(3)的余数......此时是m=3,如果m不确定的话将由这样的规律一直延续下去,应为k<=m,所以p的个数只有m个。这里我们发现p1,p2,p3.....pm,就与上图矩阵c1,c2,c3...cm不谋而合,这也是开始设置mag_in时要在后缀中加上m个【0】的原因,是为了方便储存m个pi,也防止综合除法时将每步算出的余数覆盖上原来的数据di。
该图的大概原理就是酱紫。接下来我们要了解生成多项式g(x),以及它背后的功臣a^0,a^1等等幂指数代表的有限域GF(2^m),明日更。