【python】Reed-solomon codes的二维码应用（二）

（注：本部分博客主要结合周老师的PPT以及查找的资料，尝试去解释Reed-Solomon Codes的数学原理和信息论原理，并讨论Reed-Solomon Codes在QR二维码方面的应用。）

今天我们来讨论下伽罗华域GF（2^m），它其实就可以看作 mod(2^m)，我们接触过微机原理都多多少少了解m位长的二进制数可以表示2^m个数，而一般数据码纠删码都是8bit为一单位，所以他们都属于GF（2^8）中的符号。那么我们用2^8就行了，为什么要用mod（求余）呢？这就是伽罗华域的一个特征了，任何数除以2^m的余数都会小于2^m，所以mod（2^m）的数值一定也属于伽罗华域GF（2^m）。

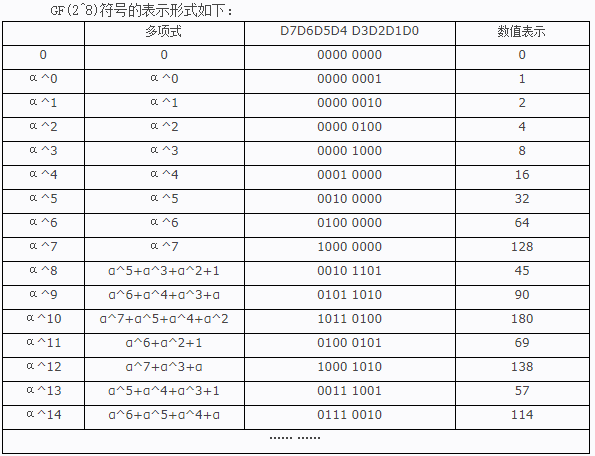
那么伽罗华域的方便之处在哪呢？先上找的图：

先解释一下，第二列和第三列是对应的，当a=2时，第二列就是将第三列中的二进制，转化为十进制的过程，比如0000 0100 = 2^7*0+2^6*0+2^5*0+2^4*0+2^3*0+2^2*1+2^1*0+2^0*0。第一列和（第二列，第三列）是给出的表格，它是由二进制基于对数的乘法算出来的（后面会细说）。最后一列就是第三列的二进制转化的十进制。（这里需要注意一下，第一列的a^k，k的空间大小为254，最后一列的数值取在[0,255)中。）

说到有限域必须解释一下域的概念。域有单位元和逆元的概念，这使它能够加或者乘，两者都是通过矩阵运算可以得到相应的结果，域的加用“^”（类似于XOR异或）表示，乘用“*”表示（但并不是我们平常认识的加与乘运算）。对于加和乘来说他们都有各自的单位矩阵e(加与乘不相等，加的单位矩阵为0，乘的单位矩阵为1），但单位矩阵有什么用呢？比如我们知道倒数，a=1/b，当我们想除以一个数的时候，就乘以这个数的倒数，类似的，已知域中c*d=e（即c和d相乘等于单位矩阵），如果我们想除以c，那么我们可以乘以c的逆元d。

伽罗华域也是如此。

我们要用伽罗华域进行多项式的加减乘除，就必须知道伽罗华域的多项式（第二列）是如何进行四则运算的。

1.对于加法和减法，我们以a^11= x^6+x^2+1，以及a^2= x^2来举个栗子：

1）进行合并同类项时，我们将1*x^2+1*x^2 = (1+1)*x^2=0*x^2=0，可以看出加法是用异或来表示，即1+1 =0，1+0=1，0+0=0。

2）进行减法的时候，减就是加法，即也是异或。

2.对于乘法，我们用0001001 x 00101010 来举栗：（^为异或，*为相乘）

        10001001
 *      00101010
   -------------
       10001001
 ^   10001001
 ^ 10001001
   -------------
   1010001111010

用Python来描述就是：

def poly_mult(x,y):
 z = 0
 i = 0
 while (y>>i) > 0:       #指针从y的最右侧开始右移i位，只要除数内还有1，就继续执行
   if y & (1<<i):         #判断y右移了i位后的右边第一位是否为1，如果为1则将x与z异或
     z ^= x<<i            #将x错位，统一阶位
   i += 1
 return z

（解释一下，这里的>>右移符号位是相对二进制来说的，>>i是指二进制数右移了i位，对于二进制来说，右移i位代表该数除以2^i，具体功能请看函数poly_mult()的注释。）

当然还有更高效的方法，比如俄罗斯农夫法Russian Peasant 算法（战斗种族连农夫这么强的吗。。。）：

def gf_mult_RU(x, y):     
    r = 0    
    while y:           #判断y>0
        if y & 1:          #判断y是否是奇数
            r = r ^ x      #主要是将上一次的x存储起来并异或
            y = y >> 1     #将y除以2，由于它是奇数y基于二进制右移的，右移代表在减去最后一位1后顺便除以2，这就十分666了，为农夫打call     
            x = x << 1      #将x乘以2   
    return r

这样子通过不断地循环：

x*y = (x*2) * (y/2)

x*y = (x*2) * (y-1)/2 + x

最终y<0时，r就是两者的乘积。了解了多项式乘法后当然还有除法啦，主要是十分优雅的高斯消元法，明天更。

【python】Reed-solomon codes的二维码应用（二）

猜你喜欢