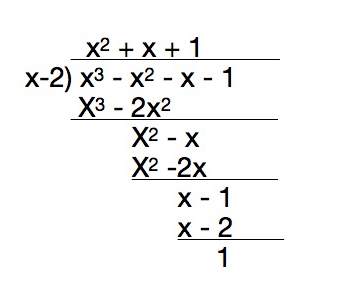【python】Reed-solomon codes的二维码应用（四）

4.除法

对于多项式来说主要运用综合除法(synthetic division)这一高效的算法来实现，在讲综合除法之前先复习一下长除法：

例：f(x) = x³ - x² - x - 1

把f(x)展开基于偏移a的泰勒表达式：c₀ + c₁(x-a) + c₂(x-a)² + c₃(x-a)³

假设偏移值a=2

上述的f(x) 展开= 1 + 7(x-2) + 5(x-2)² + (x-a)³

即c₀= 1, c₁ = 7, c₂ = 5, c₃ = 1

我们可以通过长除法分别计算出c_0,c_1,c_2,c₃

得到余数1即c₀, 再重复两次计算(x2 + x + 1) / (x-2) = (x + 3) … 7, (x + 3) / (x-2) = 1 … 5

所有的系数c₀到c₃全部计数结束

通过综合除法也可以得到相同的结果，但计算方式要比上面简单很多

仍然以上面f(x)为例，通过综合除法求得c_0,c_1,c_2,c₃

第一步把 x³, -x², -x, -1的系数提取出来，把x-a的-a 乘以-1放到最右边

计算步骤如：

第1排第一个数不变往下移到第2排
第2排的第1个数1 * 2 和第1排的第2个数相加得到第2排的第2个数，
第2排的第2个数 1 * 2和第1排第3个数相加得到第2排的第3个数，
第2排的第3个数 1 * 2和第1排第4个数相加得到第2排的第4个数

第2排最后一个数即为余数，余数不参数后继计算。以上为一次综合除法的步骤，第三排的数由第二次综合除法求得。

下面的代码是该算法对GF(2^p)多项式的一个扩展实现：

def gf_poly_div(dividend, divisor):
    '''适用于GF(2^p)域的快速多项式除法.'''
   
    msg_out = list(dividend) # 复制被除数(尾部后缀ecc字节, 用0填充)
    #normalizer = divisor[0] # precomputing for performance
    for i in range(0, len(dividend) - (len(divisor)-1)):
        #msg_out[i] /= normalizer 
        coef = msg_out[i]
        if coef != 0: # 避免log(0)未定义错误.
            for j in range(1, len(divisor)): # 因为多项式的首位都是1, (1^1==0)所以可以跳过
                if divisor[j] != 0: # log(0) is undefined
                    msg_out[i + j] ^= gf_mul(divisor[j], coef) # 等价于数学表达式:msg_out[i + j] += -divisor[j] * coef ,但异或运高效

    # msg_out 包含商和余数, 余数的最高幂次( == length-1)和除数一样, 下面计算分断点.
    separator = -(len(divisor)-1)
    return msg_out[:separator], msg_out[separator:] # 返回商, 余数

【python】Reed-solomon codes的二维码应用（四）

猜你喜欢