今天对RS编码做最后的补充和总结,可以比较完整地回顾和解答我们第一部分提出的问题了!
对于RS的编码矩阵,我们通过综合除法可得列表[Qm,Rm-1,Rm-2,.......R2,R1,R0],但我们还需要将Qm替换成原来的数据[D0,D1.....Dn],即最后生成[D0,D1,D2....Dn,Rm-1,Rm-2,.......R2,R1,R0],这个才是我们最后可以保存的数据,具体代码如下:
def rs_encode_msg(msg_in, nsym):
gen = rs_generator_poly(nsym)
# 用msg_in值初始化 msg_out 并后缀ecc字节, 用0填充.
msg_out = [0] * (len(msg_in) + len(gen)-1)
msg_out[:len(msg_in)] = msg_in
# Synthetic division main loop
for i in range(len(msg_in)):
coef = msg_out[i]
if coef != 0: # 避免log(0) 未定义错误
for j in range(1, len(gen)): # 因为多项式的首位都是1, (1^1==0)所以可以跳过
msg_out[i+j] ^= gf_mul(gen[j], coef) # equivalent to msg_out[i+j] += gf_mul(gen[j], coef)
# 除完之后, msg_out 包含商 msg_out[:len(msg_in)],余数 msg_out[len(msg_in):].
#RS码只用到余数, 所以我们用原信息覆盖商得到完整编码.
msg_out[:len(msg_in)] = msg_in
return msg_out
对应的RS码还是下图:
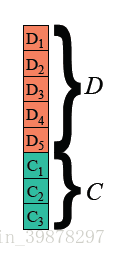
其中矩阵 C就是RS码求得的余数[R2,R1,R0],矩阵D是原数据[D1,D2,D3,D4,D5],现在我们已经从伽罗华域到生成多项式到综合除法再到BCH码了解了许多可以窥见RS编码原理的知识,那么我们现在回到第一部分,回答当时我们忽略的思考,为什么要做成[D0,D1,D2....Dn,Rm-1,Rm-2,.......R2,R1,R0]这个矩阵呢?
我们从上面的代码可得我们在原数据[D1,D2,D3,D4,D5]后缀加上[0,0,0],成为[D1,D2,D3,D4,D5,0,0,0],然后我们通过综合除法得到[Q1,Q2,Q3,Q4,Q5,R2,R1,R0](其中列表[Q1,Q2,Q3,Q4,Q5]代表商的多项式),然后我们会使用这个代码:
#RS码只用到余数, 所以我们用原信息覆盖商得到完整编码.
msg_out[:len(msg_in)] = msg_in
于是我们就把编码变成[D1,D2,D3,D4,D5,R2,R1,R0],那么我们编成这样有什么用呢?
在这里就必须一直结合之前说过的内容啦!还记得我们接触BCH码时怎样求余的吗?
def qr_check_format(fmt):
g = 0x537 # = 0b10100110111 in python 2.6+
for i in range(4,-1,-1):
if fmt & (1 << (i+10)): # 判断是否为1
fmt ^= g << i
return fmt
最后得到的fmt就是输入的原fmt除以生成多项式得到的余数,利用这个代码我们可以将其应用于检查错误,检查错误的代码如下(下面的这个fmt与上面的那个fmt无关,没有衔接):
encoded_format = (format<<10) ^ qr_check_format(format<<10)
我们将除数生成多项式看作G,被除数(fmt<<10)看作F,函数qr_check_format(format<<10)的作用是将F/G,得到商看作Q,余数看作R,这个函数最后输出的是R。所以式子(format<<10) ^ qr_check_format(format<<10)可以翻译为最后的编码encoded_format= F ^ R
我们知道关系式F = Q*G +R,所以对于 F^R = (Q*G +R )^R,由于在伽罗华域中异或^既可以表示加法也可以表示减法,所以我们得到 F^R = (Q*G +R )^R = Q*G +R -R = Q *G
Q是商我们可以忽略它,但是G代表了生成多项式,也就是说最后的编码encoded_format能被生成多项式G整除!
但是我们不是再将RS码吗?为什么说到了这个编码?
这个才是RS编码过程最巧妙!最性感!令人疯狂打call的地方啊啊啊啊啊!
在RS编码过程中,我们之前将原fmt后缀加上列表[0,0,...0],发现这个东西是否似曾相识?!
没错!我们可以充分联想到之前的 encoded_format = (format<<10) ^ qr_check_format(format<<10),这个format<<10是指相对于二进制的左移10位,后面用零填充,这是否与原fmt后缀加上列表[0,0,...0]有异曲同工之妙??!!我们将得到的新fmt用综合除法的到余数[Rm-1,Rm-2,.......R2,R1,R0],最后我们将原fmt覆盖上[Q1,Q2,Q3...Qn,Rm-1,Rm-2,.......R2,R1,R0]的商的部分,得到RS编码[D1,D2,D3...Dn,Rm-1,Rm-2,.......R2,R1,R0]。
再结合解释一下,RS码 = [D1,D2,D3...Dn,Rm-1,Rm-2,.......R2,R1,R0] = [D1,D2,D3...Dn,0,0,...0] ^ [Rm-1,Rm-2,.......R2,R1,R0] = ( fmt+后缀[0,0,..0] ) ^ 求余 ( fmt+后缀[0,0,..0] )
它与上面的encoded_format = (format<<10) ^ qr_check_format(format<<10)一一对应啊!!!为发明这个码的作者疯狂打call把!!!!
最后我们得到的RS码就是Q(x)*G(x),即RS码是可以被生成多项式G(x)整除的!这就是我们为什么要变成这个矩阵的原因了,因为这个特性在后面RS码的译码部分会有很大用处!
RS编码部分完结,明天说RS译码。