考研 | 高等数学 Chapter4 不定积分
文章目录
I. 定义
- 原函数 — If F ′ ( x ) = f ( x ) , F ( x ) 称为 f ( x ) 原函数 F'(x)=f(x), F(x) 称为 f(x) 原函数 F′(x)=f(x),F(x)称为f(x)原函数
- 不定积分 — 设 F ( x ) 为 f ( x ) 的一个原函数 , F ( x ) + C 称为 f ( x ) 的不定积分 F(x) 为 f(x)的一个原函数, F(x)+C 称为f(x)的不定积分 F(x)为f(x)的一个原函数,F(x)+C称为f(x)的不定积分
- Notes:
- 若 f ( x ) ∃ ⇒ ∃ f(x) \exists\ \ \Rightarrow\exists f(x)∃ ⇒∃无数个原函数
- 任意两个原函数之差为常数
- 若 f ( x ) 连续 ⇒ ∃ f(x) 连续\ \ \Rightarrow\ \ \exists f(x)连续 ⇒ ∃原函数
II. 不定积分工具
a. 基本公式
- ∫ k d x = k x + C \int k dx=kx+C ∫kdx=kx+C
- 幂函数
- ∫ x a d x = 1 a + 1 x a + 1 + C ; ( a ≠ 1 ) \int x^a dx=\frac{1}{a+1}x^{a+1}+C;\quad (a \neq 1) ∫xadx=a+11xa+1+C;(a=1)
- ∫ 1 x d x = ln ∣ x ∣ + C \int \frac1x dx=\ln |x|+C ∫x1dx=ln∣x∣+C
- 指数函数
- ∫ a x d x = a x ln a + C ; ( a ≠ 1 ) \int a^x dx=\frac{a^x}{\ln a} + C;\quad (a \neq 1) ∫axdx=lnaax+C;(a=1)
- ∫ 1 x d x = x + C \int 1^x dx=x+C ∫1xdx=x+C
- 三角函数
∫ sin x d x = − cos x + C \int \sin x dx = -\cos x + C ∫sinxdx=−cosx+C ∫ cos x d x = sin x + C \int \cos x dx = \sin x + C ∫cosxdx=sinx+C ∫ tan x d x = − ln ∣ cos x ∣ + C \int \tan x dx = -\ln |\cos x| + C ∫tanxdx=−ln∣cosx∣+C ∫ cot x d x = ln ∣ sin x ∣ + C \int \cot x dx = \ln |\sin x| + C ∫cotxdx=ln∣sinx∣+C ∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int \sec x dx = \ln |\sec x + \tan x| + C ∫secxdx=ln∣secx+tanx∣+C ∫ csc x d x = ln ∣ csc x − cot x ∣ + C \int \csc x dx = \ln |\csc x-\cot x| + C ∫cscxdx=ln∣cscx−cotx∣+C ∫ sec 2 x d x = tan x + C \int \sec ^2x dx = \tan x + C ∫sec2xdx=tanx+C ∫ csc 2 x d x = − cot x + C \int \csc ^2x dx = -\cot x + C ∫csc2xdx=−cotx+C ∫ sec ( tan x ) d x = sec x + C \int \sec (\tan x) dx = \sec x + C ∫sec(tanx)dx=secx+C ∫ csc x cot x d x = − csc x + C \int \csc x\cot x dx = -\csc x + C ∫cscxcotxdx=−cscx+C - 平方和平方差
∫ 1 1 − x 2 d x = arcsin x + C \int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C ∫1−x21dx=arcsinx+C ∫ 1 a 2 − x 2 d x = arcsin x a + C \int \frac{1}{\sqrt{a^2-x^2}} dx = \arcsin \frac xa + C ∫a2−x21dx=arcsinax+C ∫ 1 1 + x 2 d x = arctan x + C \int \frac1{1+x^2} dx = \arctan x + C ∫1+x21dx=arctanx+C ∫ 1 a 2 + x 2 d x = 1 a arctan x a + C \int \frac1{a^2+x^2} dx = \frac1a\arctan \frac xa + C ∫a2+x21dx=a1arctanax+C ∫ 1 x 2 + a 2 d x = ln ( x + x 2 + a 2 ) + C \int \frac1{\sqrt{x^2+a^2}} dx = \ln(x+\sqrt{x^2+a^2}) + C ∫x2+a21dx=ln(x+x2+a2)+C ∫ 1 x 2 − a 2 d x = ln ( x + x 2 − a 2 ) + C \int \frac1{\sqrt{x^2-a^2}} dx = \ln(x+\sqrt{x^2-a^2}) + C ∫x2−a21dx=ln(x+x2−a2)+C ∫ 1 x 2 − a 2 d x = 1 2 a ln ∣ x − a x + a ∣ + C \int \frac1{x^2-a^2} dx = \frac1{2a}\ln|\frac{x-a}{x+a}| + C ∫x2−a21dx=2a1ln∣x+ax−a∣+C ∫ a 2 − x d x = a 2 2 arcsin x a + x 2 a 2 − x 2 + C \int \sqrt{a^2-x} dx = \frac{a^2}{2}\arcsin\frac xa + \frac x2\sqrt{a^2-x^2} + C ∫a2−xdx=2a2arcsinax+2xa2−x2+C
b. 积分法
case1: 第一类换元积分法

case2: 第二类换元积分法
1. 无理变有理

2. 三角代换, 平方和平方差
涉及到:
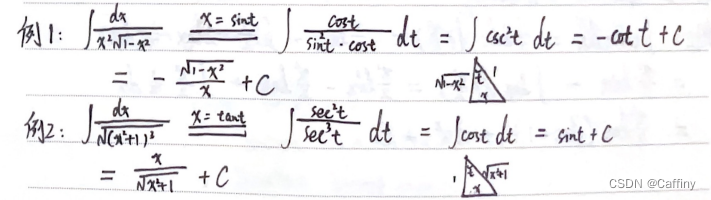
1. a 2 − x 2 ⇒ x = a sin t ⇒ a cos t \sqrt{a^2-x^2}\quad\Rightarrow\quad x=a\sin t \quad\Rightarrow\quad a\cos t a2−x2⇒x=asint⇒acost
2. a 2 + x 2 ⇒ x = a tan t ⇒ a sec t \sqrt{a^2+x^2}\quad\Rightarrow\quad x=a\tan t \quad\Rightarrow\quad a\sec t a2+x2⇒x=atant⇒asect
3. x 2 − a 2 ⇒ x = a sec t ⇒ a tan t \sqrt{x^2-a^2}\quad\Rightarrow\quad x=a\sec t \quad\Rightarrow\quad a\tan t x2−a2⇒x=asect⇒atant
3. 分部积分法
( u v ) ′ = u ′ v + u v ′ ∫ ( u v ) ′ d x = ∫ u ′ v d x + ∫ u v ′ d x u v = ∫ v d u + ∫ u d v ∫ u d v = u v − ∫ v d u \begin{aligned} (uv)'&=u'v+uv' \\ \int (uv)' dx &= \int u'v dx + \int uv'dx \\ uv &= \int v du + \int u dv \\ \int u dv &= uv - \int v du \end{aligned} (uv)′∫(uv)′dxuv∫udv=u′v+uv′=∫u′vdx+∫uv′dx=∫vdu+∫udv=uv−∫vdu
-
∫ 幂 ∗ 指 d x \int 幂*指 dx ∫幂∗指dx, 留幂函数
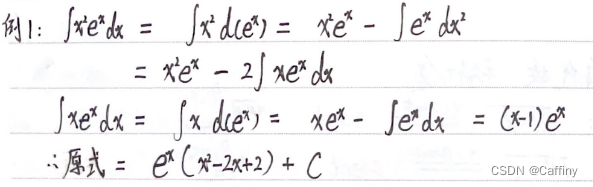
-
∫ 幂 ∗ 对数 d x \int 幂*对数 dx ∫幂∗对数dx, 留对数

-
∫ 幂 ∗ 三角 d x \int 幂*三角 dx ∫幂∗三角dx
Notes:- 三角函数 sin cos \sin\cos sincos必须是一次
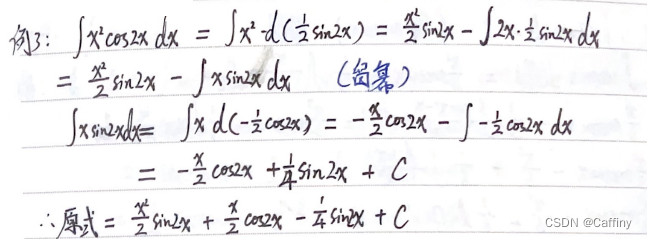
- 如果遇到 sin 2 cos 2 \sin^2\cos^2 sin2cos2用半角公式降次
sin ( 2 x ) = 2 sin x cos x cos ( 2 x ) = cos 2 x + sin 2 x \sin(2x)=2\sin x\cos x \\\cos(2x)=\cos^2 x + \sin^2 x sin(2x)=2sinxcosxcos(2x)=cos2x+sin2x
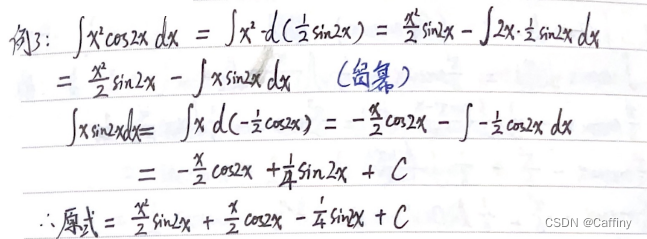
- 如果遇到 tan cot sec cot \tan\cot\sec\cot tancotseccot等可以允许偶数次

- 三角函数 sin cos \sin\cos sincos必须是一次
-
∫ 幂 ∗ 反三角 d x \int 幂*反三角 dx ∫幂∗反三角dx, 留反三角函数

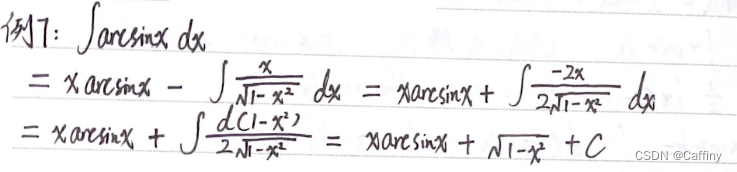
-
∫ e a x ∗ sin b x \int e^{ax}*\sin bx ∫eax∗sinbx 或 ∫ e a x ∗ cos b x \int e^{ax}*\cos bx ∫eax∗cosbx, 留三角函数
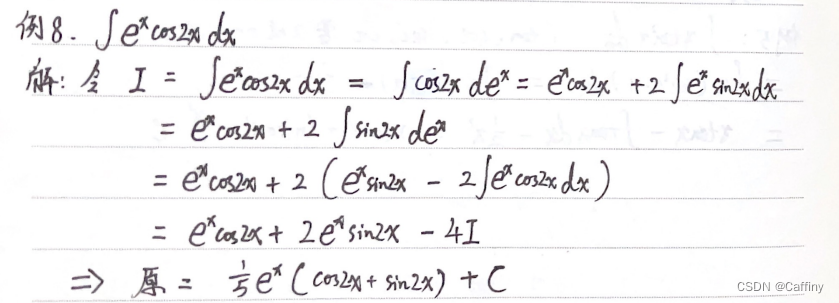
-
∫ sec n x d x \int \sec^nx dx ∫secnxdx 或 ∫ csc n x d x \int \csc^n xdx ∫cscnxdx, 其中 n n n 为奇数
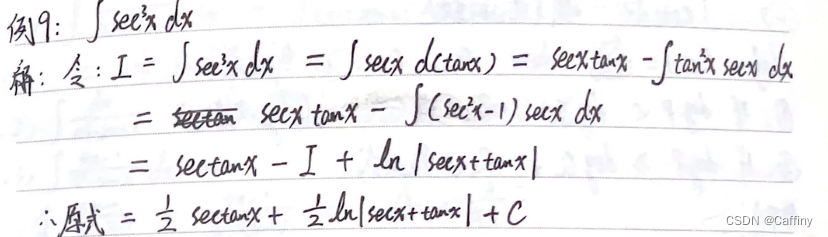
-
∫ sec n x d x \int \sec^nx dx ∫secnxdx 或 ∫ csc n x d x \int \csc^n xdx ∫cscnxdx, 其中 n n n 为偶数
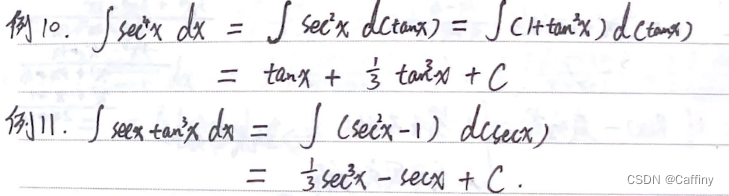
III. 特殊函数的不定积分
a. 有理函数
定义: 被积函数 R ( x ) R(x) R(x) 为有理函数, 其中 R ( x ) = P ( x ) Q ( x ) R(x)=\frac{P(x)}{Q(x)} R(x)=Q(x)P(x), 其中 P ( x ) Q ( x ) P(x)Q(x) P(x)Q(x) 分别为多项式
当 P ( x ) 最大次数 < Q ( x ) 最大次数 P(x)最大次数 < Q(x)最大次数 P(x)最大次数<Q(x)最大次数, R ( x ) R(x) R(x) 为真分式
当 P ( x ) 最大次数 ≥ Q ( x ) 最大次数 P(x)最大次数 \geq Q(x)最大次数 P(x)最大次数≥Q(x)最大次数, R ( x ) R(x) R(x) 为假分式
case1: 假分式
思路: 将假分式转成多项式+真分式

case2: 真分式
思路: 1. 分子不动; 2. 分母因式分解拆成部分和
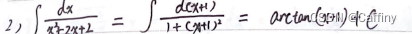
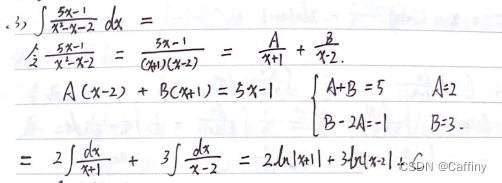
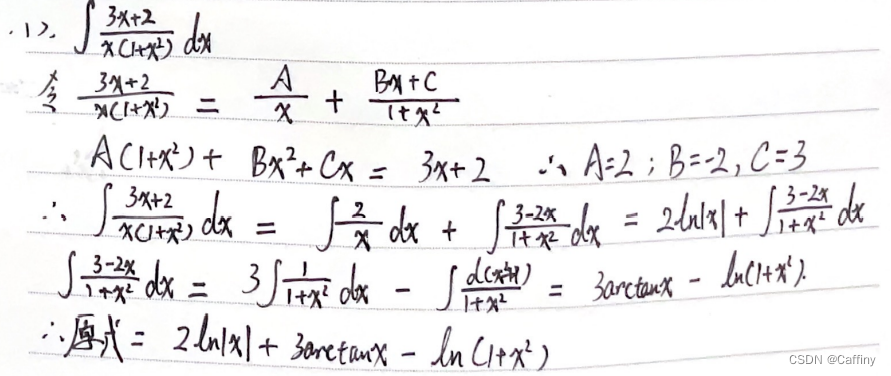
b. 无理函数
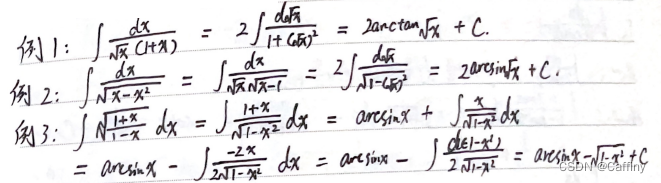
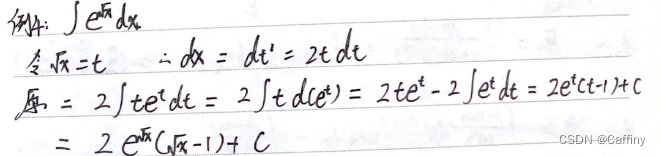
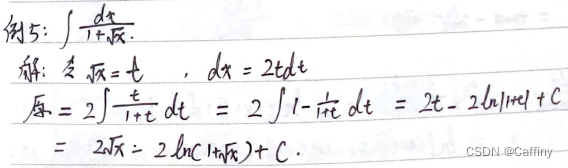
c. 三角有理函数不定积分
