在GAMS101的第二节课的末尾,闫老师在讲解了向量的基本知识之后,引入了矩阵Matrices。
1)矩阵和向量相乘

将向量视为列向量(即的矩阵),矩阵在左边,向量在右边。
举例:在二维平面中,将向量作y轴对称操作。
给定任一一点(x,y),将y轴作为对称轴时,对称的点是(-x,y).
如果此时我们有一矩阵,将这一矩阵乘以向量(x,y),我们会得到
这样,我们就通过矩阵就实现了对向量进行y轴对称反射的操作。
向量的点乘和叉乘,我们也可以用矩阵形式表示

到了第三节课,我们主要就是学习通过矩阵来实现图形的变换。
在图形学中,矩阵广泛用于表示转换。(In Graphics,pervasively used to represent transformations)
2)二维变换
Scale缩放变换
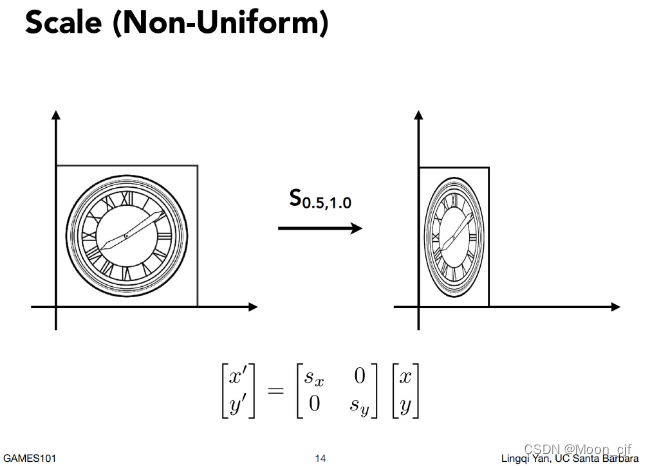
Reflection反射变换
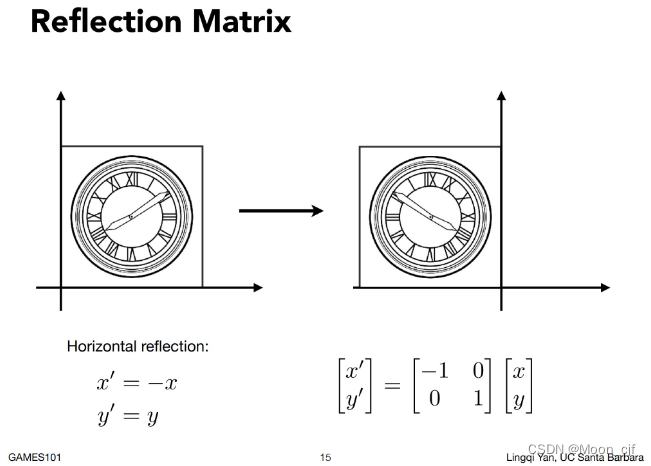
Shear剪切变换
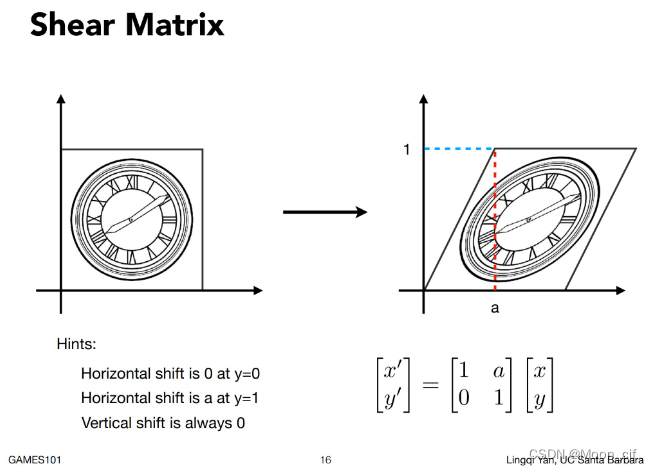
Rotate旋转变换

上述四种变换,我们以Rotate旋转变换来进行讲解。
在二维变换时,假设一个原始点(x,y),在进行某种变换后,变成了(x’,y’),写成表达式为
其中,称为变换矩阵。
在求解变换矩阵时,我们可以选取特殊的点变换前和变换后的值,带入表达式求值即可。
旋转变换,当旋转角度时,我们分别选取两个特殊的点(1,0)和(0,1),这两个点在旋转之后,变换的位置分别变成了
和
,我们带回表达式,可以得到
上述两个表达式,我们依次进行展开,得到如下:
,得到
,得到
和
,得到
,得到
将求得的值再带回表达式,我们得到
这样,我们就得到了旋转的变换矩阵。
缩放、反射、剪切、旋转四种变换,我们可以统一写成如下公式:

我们称之为线性变换(Linear Transforms)。
但是,我们再讨论Translation平移变换,我们会发现
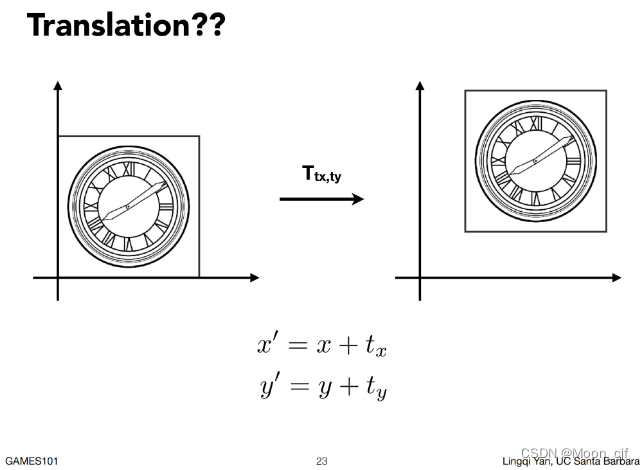
表达式为
其中,表示x和y的平移量。
为了将缩放、反射、剪切、旋转等线性变换与平移变换的非线性变换统一成一种矩阵形式,我们人为的引入了齐次坐标(Homogeneous Coordinates)。

在二维坐标中,我们增加第三个坐标。我们规定:
如果第三个坐标为1,表示一个二维的点;
如果第三个作为为0,表示一个二维向量;
我们用齐次坐标来完成上诉各种变换的统一的矩阵形式。

完成了统一的矩阵形式之后,我们就可以通过研究矩阵来研究变换的特性。
逆变换
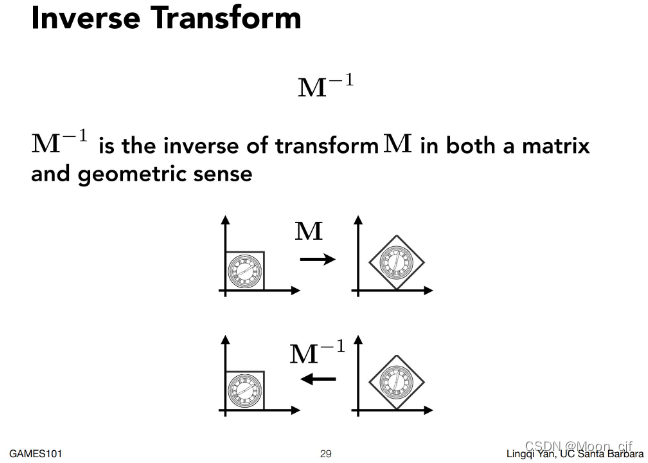
变换的组合

变换的分解

3)三维变换
在二维的基础上,我们拓展到三维。

在三维的齐次坐标上,我们统一三维的矩阵形式。
