【模板题】几种常见的Nim游戏（博弈论）

一、AcWing 891. Nim游戏

【题目描述】
给定$n$堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。

【输入格式】
第一行包含整数$n$。
第二行包含$n$个数字，其中第$i$个数字表示第$i$堆石子的数量。

【输出格式】
如果先手方必胜，则输出Yes。
否则，输出No。

【数据范围】
$1\le n\le 10^5$
$1\le 每堆石子数\le 10^9$

【输入样例】

2
2 3

【输出样例】

Yes

【分析】

---

首先给出结论：若$a_1\wedge a_2\wedge \cdots \wedge a_n=0$（$a_i$表示第$i$堆石子的数量），则先手必败，否则先手必胜。

在讲$Nim$游戏之前，先了解一下什么是公平组合游戏$(ICG)$。若一个游戏满足以下条件，则该游戏称为公平组合游戏：

• 由两名玩家交替行动
• 在游戏进行的任意时刻，可以执行的合法行动与轮到哪位玩家无关
• 不能行动的玩家判负

$Nim$游戏属于公平组合游戏，但常见的棋类游戏，比如围棋就不是公平组合游戏，因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件$2$和$3$。

---

什么是先手必胜状态和先手必败状态？

• 先手必胜状态：先手进行某一个操作，留给后手是一个必败状态时，对于先手来说是一个必胜状态。即先手可以走到某一个必败状态。
• 先手必败状态：先手无论如何操作，留给后手都是一个必胜状态时，对于先手来说是一个必败状态。即先手走不到任何一个必败状态。

---

为什么当$a_1\wedge a_2\wedge \cdots \wedge a_n=0$时先手必败，否则先手必胜？

1. 当到达结束状态时，即无法再进行任何操作，此时$0\wedge 0\wedge \cdots \wedge 0=0$；
2. 如果其中某一个状态$a_1\wedge a_2\wedge \cdots \wedge a_n=x$（$x$不为$0$），那么一定有一种拿法能够使得剩下的数异或值为$0$。证明如下：
   假设$x$的二进制表示里最高的一位$1$在第$k$位，则$a_1\sim a_n$中至少有一个数$a_i$的第$k$位是$1$（如果全为$0$那么$x$的第$k$位一定是$0$），那么显然$a_i\wedge x<a_i$，所以我们可以从中拿走$a_i-(a_i\wedge x)$个石子，那么第$i$堆石子就剩$a_i-(a_i-(a_i\wedge x))=a_i\wedge x$个，即原式变为：$a_1\wedge a_2\wedge \cdots \wedge (a_i\wedge x)\wedge \cdots \wedge a_n$。由于$a_1\wedge a_2\wedge \cdots \wedge a_i\wedge \cdots \wedge a_n=x$，因此上式变为$x\wedge x=0$。
3. 如果其中某一个状态$a_1\wedge a_2\wedge \cdots \wedge a_n=0$，那么不管怎么拿，剩下所有数的异或值一定不为$0$，用反证法证明如下：
   假设第$i$堆拿走一部分石子后剩余石子数为$a_i^{\prime }$，且$a_1\wedge a_2\wedge \cdots \wedge a_i^{\prime }\wedge \cdots \wedge a_n=0$，而由于已知原状态为$a_1\wedge a_2\wedge \cdots \wedge a_i\wedge \cdots \wedge a_n=0$，将两个式子进行异或，由于除了$a_i、a_i^{\prime }$以外其余数都是成对出现，异或值为$0$，因此结果为$a_i\wedge a_i^{\prime }=0$，所以$a_i=a_i^{\prime }$，又由于假设第$i$堆已经拿走一部分石子了，与$a_i=a_i^{\prime }$矛盾，因此假设不成立，原命题成立。

综上，当先手局面为$a_1\wedge a_2\wedge \cdots \wedge a_n=0$时抛给后手的状态一定为$a_1\wedge a_2\wedge \cdots \wedge a_n\ne 0$，当先手局面为$a_1\wedge a_2\wedge \cdots \wedge a_n\ne 0$时抛给后手的状态一定是$a_1\wedge a_2\wedge \cdots \wedge a_n=0$。所以当$a_1\wedge a_2\wedge \cdots \wedge a_n=0$时先手必败，否则先手必胜。

---

【代码】

#include <iostream>
using namespace std;

int main()
{
    
    
	int n, res = 0;
	cin >> n;
	while (n--)
	{
    
    
		int x;
		cin >> x;
		res ^= x;
	}
	if (res) puts("Yes");
	else puts("No");
	return 0;
}

二、AcWing 892. 台阶-Nim游戏

【题目描述】
现在，有一个$n$级台阶的楼梯，每级台阶上都有若干个石子，其中第$i$级台阶上有$a_i$个石子$(i\ge 1)$。
两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。
已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。

【输入格式】
第一行包含整数$n$。
第二行包含$n$个整数，其中第$i$个整数表示第$i$级台阶上的石子数$a_i$。

【输出格式】
如果先手方必胜，则输出Yes。
否则，输出No。

【数据范围】
$1\le n\le 10^5$
$1\le a_i\le 10^9$

【输入样例】

3
2 1 3

【输出样例】

Yes

【分析】

---

结论：当奇数级阶梯的石子数量异或值为$0$，即$a_1\wedge a_3\wedge \cdots \wedge a_{2n-1}=0$时，先手必败，否则先手必胜。证明思路同经典$Nim$游戏相似。

---

【代码】

#include <iostream>
using namespace std;

int main()
{
    
    
    int n, res = 0;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
    
    
        int x;
        cin >> x;
        if (i % 2) res ^= x;
    }
    if (res) puts("Yes");
    else puts("No");
    return 0;
}

三、AcWing 893. 集合-Nim游戏（SG函数）

【题目描述】
给定$n$堆石子以及一个由$k$个不同正整数构成的数字集合$S$。
现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合$S$，最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。

【输入格式】
第一行包含整数$k$，表示数字集合$S$中数字的个数。
第二行包含$k$个整数，其中第$i$个整数表示数字集合$S$中的第$i$个数$s_i$。
第三行包含整数$n$。
第四行包含$n$个整数，其中第$i$个整数表示第$i$堆石子的数量$h_i$。

【输出格式】
如果先手方必胜，则输出Yes。
否则，输出No。

【数据范围】
$1\le n,k\le 100$
$1\le s_i,h_i\le 10000$

【输入样例】

2
2 5
3
2 4 7

【输出样例】

Yes

【分析】

---

（1）Mex运算：
设$S$表示一个非负整数集合，定义$mex(S)$为求出不属于集合$S$的最小非负整数运算，即：
m e x ( S ) = m i n { x } mex(S)=min\left\{x\right\} mex(S)=min{ x}；
例如： S = { 0 , 1 , 2 , 4 } S=\left\{0,1,2,4\right\} S={ 0,1,2,4}，那么$mex(S)=3$。

---

（2）SG函数
在有向图游戏中，对于每个节点$x$，设从$x$出发共有$k$条有向边，分别到达节点$y_1,y_2,\dots ,y_k$，定义$SG(x)$为$x$的后继节点$y_1,y_2,\dots ,y_k$的$SG$函数值构成的集合执行$mex$运算的结果，即：
S G ( x ) = m e x ( { S G ( y 1 ) , S G ( y 2 ) , … , S G ( y k ) } ) SG(x)=mex(\left\{SG(y_1),SG(y_2),\dots ,SG(y_k)\right\}) SG(x)=mex({ SG(y1​),SG(y2​),…,SG(yk​)})
特别地，整个有向图游戏$G$的$SG$函数值被定义为有向图游戏起点$s$的$SG$函数值，即：$SG(G)=SG(s)$。
定义终点的$SG$函数值为$0$。

---

（3）有向图游戏的和
设$G_1,G_2,\dots ,G_m$是$m$个有向图游戏。定义有向图游戏$G，$他的行动规则是任选某个有向图游戏$G_i$，并在$G_i$上行动一步，$G$被称为有向图游戏$G_1,G_2,\dots ,G_m$的和。
有向图游戏的和的$SG$函数值等于它包含的各个子游戏$SG$函数的异或和，即：
$SG(G)=SG(G_1)\wedge SG(G_2)\wedge \cdots \wedge SG(G_m)$。

---

（4）结论

• 对于一个图$G$，如果$SG(G)\ne 0$，则先手必胜，反之必败。
  证明：根据$mex$运算的定义可知，如果$SG(G)\ne 0$，那么其连接的一点必为$0$（如果其后继结点的值均不为$0$，那么该点的$mex$结果必定为$0$），当走到$SG$值为$0$的这一点时，由于$mex$运算，该结点所连接的结点的$SG$值必定不为$0$。又因为终点状态的$SG$值为$0$，所以只要先手的$SG$值不为$0$，便可以一直走向$SG$值为$0$的状态，最终走向终点。
• 对于$n$个图，如果$SG(G_1)\wedge SG(G_2)\wedge \cdots \wedge SG(G_n)\ne 0$，则先手必胜，反之必败。

---

例子：假设有一堆石子，石子数量为$10$，每次可以拿走$2$个或$5$个，那么其有向图如下图所示：

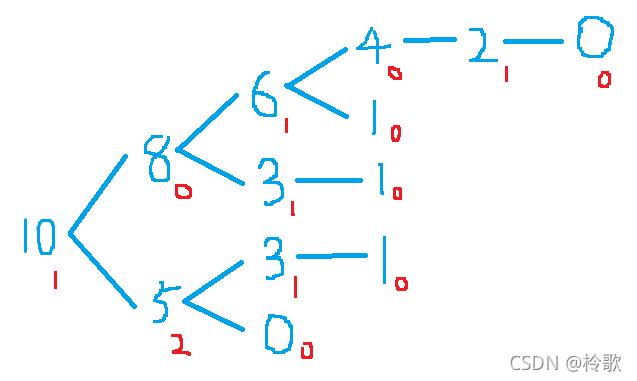
红色标注的数字为该结点的$SG$函数值，由于起点$10$的$SG$函数值不为$0$，因此该游戏局面为先手必胜状态。

---

【代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;

const int N = 110, M = 10010;
int s[N], f[M];
int n, k;

//记忆化搜索保存各结点的SG值
int sg(int x)
{
    
    
	if (~f[x]) return f[x];
	unordered_set<int> st;//保存x能到达的后继结点的SG值
	//枚举x能到达的所有状态
	for (int i = 0; i < k; i++)
		if (s[i] <= x) st.insert(sg(x - s[i]));
	//mex操作，找出x后继结点中未出现过的最小的非负整数
	for (int i = 0; ; i++)
		if (!st.count(i))
			return f[x] = i;
}

int main()
{
    
    
	cin >> k;
	for (int i = 0; i < k; i++) cin >> s[i];
	memset(f, -1, sizeof f);
	int res = 0;
	cin >> n;
	while (n--)
	{
    
    
		int x;
		cin >> x;
		res ^= sg(x);//对每个有向图的起始结点的SG值进行异或运算
	}
	if (res) puts("Yes");
	else puts("No");
	return 0;
}

四、AcWing 894. 拆分-Nim游戏

【题目描述】
给定$n$堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为$0$，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。

【输入格式】
第一行包含整数$n$。
第二行包含$n$个整数，其中第$i$个整数表示第$i$堆石子的数量$a_i$。

【输出格式】
如果先手方必胜，则输出Yes。
否则，输出No。

【数据范围】
$1\le n,a_i\le 100$

【输入样例】

2
2 3

【输出样例】

Yes

【分析】

---

相比于集合$Nim$游戏，这里的每一堆可以变成小于原来那堆的任意大小的两堆。
即$a[i]$可以拆分成$(b[i],b[j])$，为了避免重复规定$b[i]\ge b[j]$，即：$a[i]>b[i]\ge b[j]$。
相当于一个局面拆分成了两个局面，由$SG$函数理论，多个独立局面的$SG$值，等于这些局面$SG$值的异或和。
因此需要存储的状态就是$sg(b[i])\wedge sg(b[j])$。

---

【代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;

const int N = 110;
int f[N];
int n;

int sg(int x)
{
    
    
	if (~f[x]) return f[x];
	unordered_set<int> st;
	//枚举x可变成的所有状态(i, j)，防止重复j只用枚举到i即可
	for (int i = 0; i < x; i++)
		for (int j = 0; j <= i; j++)
			st.insert(sg(i) ^ sg(j));
	//mex操作
	for (int i = 0; ; i++)
		if (!st.count(i))
			return f[x] = i;
}

int main()
{
    
    
	cin >> n;
	memset(f, -1, sizeof f);
	int res = 0;
	while (n--)
	{
    
    
		int x;
		cin >> x;
		res ^= sg(x);
	}
	if (res) puts("Yes");
	else puts("No");
	return 0;
}