无监督学习定义
在聚类问题中,我们给出一个训练集{x1,…,xm},期望将数据分成一些有凝聚力的“簇”。这里的xi通常属于实数;但是数据集并没有标签y给出,所以这就是一个无监督学习问题。
K-means算法
最常用的基于欧式距离的聚类算法,其认为两个目标的距离越近,相似度越大。
K的数量选择最好的办法:手动选择。
牧师-村民模型
K-means 有一个著名的解释:牧师—村民模型:
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
我们可以看到该牧师的目的是为了让每个村民到其最近中心点的距离和最小。
算法原理
该算法的内环重复执行两个步骤:
(i)将每个训练示例x(i)“分配”到最近的聚类质心µj,
(ii)将每个聚类质心µj移动到分配给它的点的平均值。
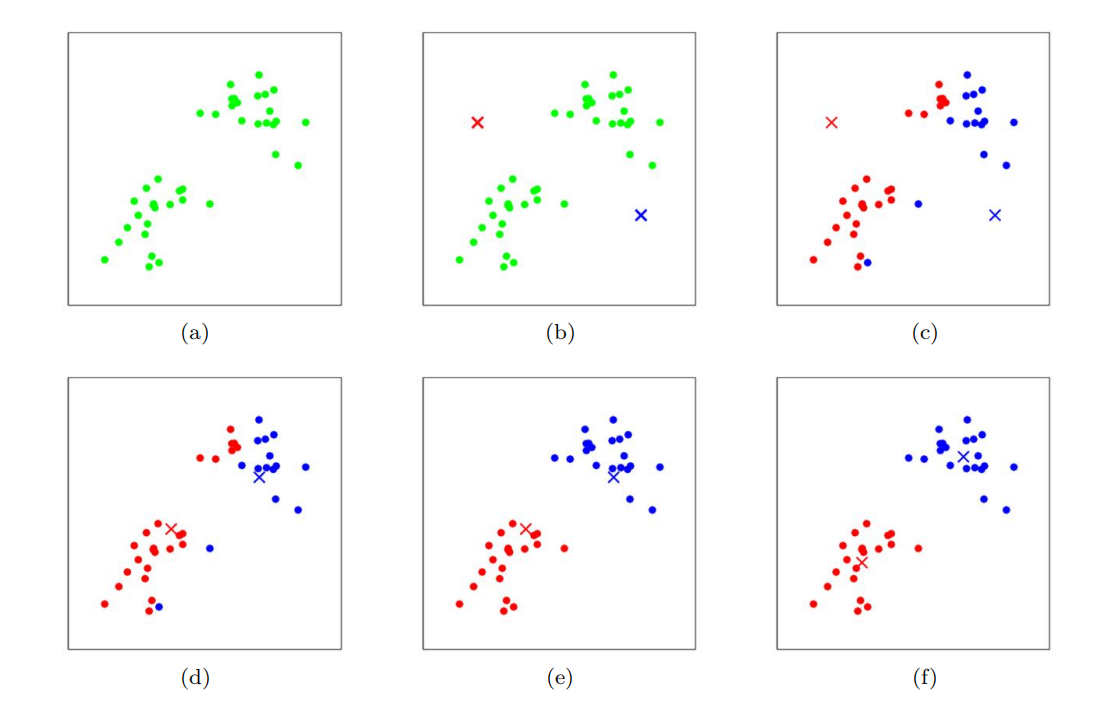
训练例子以点表示,簇质心以叉表示。(a)原始数据集。(b)随机初始聚类质心(在本例中,不选择等于两个训练示例)。(c-f)运行k-means的两次迭代的说明。在每次迭代中,我们将每个训练示例分配给最近的聚类质心(通过“绘制”训练示例与分配给的聚类质心相同的颜色显示);然后我们将每个聚类质心移动到分配给它的点的平均值。(最佳颜色颜色)
缺点
失真函数J是非凸函数,因此在J上的坐标下降不能保证收敛到全局最小值。换句话说,k-means可能容易受到局部最优值的影响。通常k-means可以正常工作,尽管如此,它还是能想出非常好的集群。但是,如果您担心陷入糟糕的局部最小值,一个常见的事情是运行k-均值多次(使用不同的随机初始值µj)。然后,从所有发现的不同的聚类中,选出失真J(c,µ)最低的一个。
算法流程

https://zhuanlan.zhihu.com/p/78798251
周志华《机器学习》
https://wuxian.blog.csdn.net/article/details/80107795
混合高斯算法(*未理解)
GMM模型
高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。

EM算法(Expectation-Maximization algorithm):
EM算法是一种迭代算法,主要有两个步骤。应用于我们的问题,在e步中,它试图“猜测”z(i)的值。在m步中,它根据我们的猜测更新了我们模型的参数。因为在m步中,我们假装第一部分的猜测是正确的,所以最大化就变得容易了。
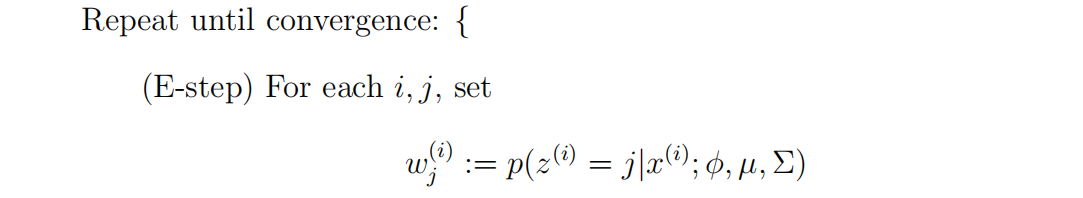

在e步骤中,我们计算我们的参数z(i)的后验概率,给定x(i),并使用我们的参数的当前设置。
李航老师《统计学习方法》
https://blog.csdn.net/xmu_jupiter/article/details/50889023
两算法异同点
GMM:
- 先计算所有数据对每个分模型的响应度
- 根据响应度计算每个分模型的参数
- 迭代
K-means:
- 先计算所有数据对于K个点的距离,取距离最近的点作为自己所属于的类
- 根据上一步的类别划分更新点的位置(点的位置就可以看做是模型参数)
- 迭代
可以看出GMM和K-means还是有很大的相同点的。GMM中数据对高斯分量的响应度就相当于K-means中的距离计算,GMM中的根据响应度计算高斯分量参数就相当于K-means中计算分类点的位置。然后它们都通过不断迭代达到最优。不同的是:GMM模型给出的是每一个观测点由哪个高斯分量生成的概率,而K-means直接给出一个观测点属于哪一类。
https://blog.csdn.net/xmu_jupiter/article/details/50889023
簇
聚类是典型的无监督学习方法,通过无标记的训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。常见的其他无监督学习任务还有密度估计、异常检测等。
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”(cluster)。通过这样的划分每个簇可能对应于一些潜在的概念,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇所对应的概念语义需由使用者来把握和命名。
https://zhuanlan.zhihu.com/p/70756804
高斯函数
正态分布是高斯概率分布。高斯概率分布是反映中心极限定理原理的函数,该定理指出当随机样本足够大时,总体样本将趋向于期望值并且远离期望值的值将不太频繁地出现。
高斯函数广泛应用于统计学领域,用于表述正态分布,在信号处理领域,用于定义高斯滤波器,在图像处理领域,二维高斯核函数常用于高斯模糊Gaussian Blur,在数学领域,主要是用于解决热力方程和扩散方程,以及定义Weiertrass Transform。
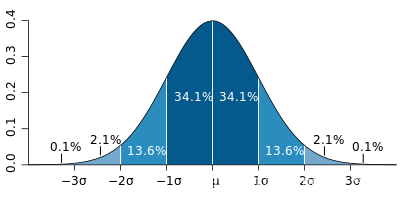
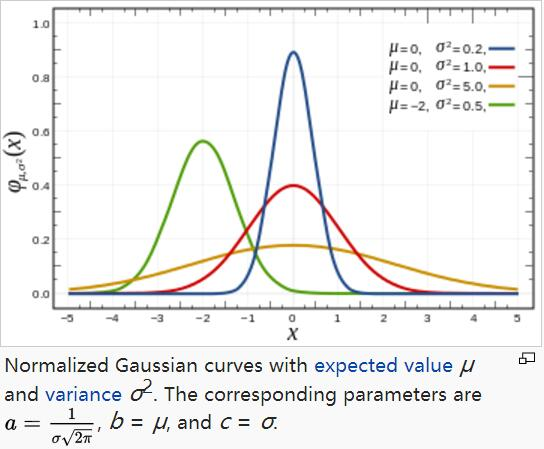
μ指的是期望,决定了正态分布的中心对称轴
σ指的是方差决定了正态分布的胖瘦,方差越大,正态分布相对的胖而矮
方差:(x指的是平均数)
标准差:方差开根号
任何正态分布的概率密度从负无穷到正无穷积分结果都为1
一维高斯函数
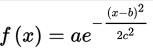
对于任意的实数a,b,c,是以著名数学家Carl Friedrich Gauss的名字命名的。高斯的一维图是特征对称“bell curve”形状,a是曲线尖峰的高度,b是尖峰中心的坐标,c称为标准方差,表征的是bell钟状的宽度。
二维高斯函数
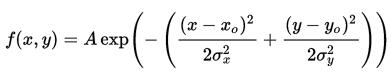
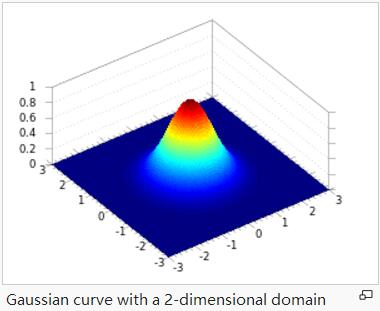
A是幅值,x。y。是中心点坐标,σx σy是方差,图示如下,A = 1, xo = 0, yo = 0, σx = σy = 1
https://blog.csdn.net/qinglongzhan/article/details/82348153
PCA算法(Principal components analysis)
主成分分析(PCA),它也试图识别数据近似所在的子空间。PCA将更直接地做到这一点,并且只需要一个特征向量计算(使用Matlab中的eig函数很容易完成),而不需要求助于EM。
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法(非监督的机器学习方法)。
其最主要的用途在于“降维”,通过析取主成分显出的最大的个别差异,发现更便于人类理解的特征。也可以用来削减回归分析和聚类分析中变量的数目。
为什么要做主成分分析
在很多场景中需要对多变量数据进行观测,在一定程度上增加了数据采集的工作量。更重要的是:多变量之间可能存在相关性,从而增加了问题分析的复杂性。
如果对每个指标进行单独分析,其分析结果往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。
步骤
步骤(1-2)忽略数据的平均值
可以忽略对于已知平均值为零的数据(例如,与语音或其他声学信号对应的时间序列)。
(3-4)重新调整每个坐标
使其具有单位方差,以确保不同的属性都在相同的“尺度”上被处理。例如,如果x1是汽车的最大速度,单位为每里(取高十或低百),x2是座位数量(取2-4左右),那么这种重正化重新调整不同的属性,使它们更具可比性。
如果我们预先知道不同的属性都在相同的尺度上,那么就可以省略步骤(3-4)。
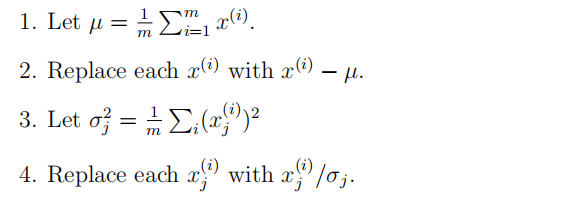
二维降一维
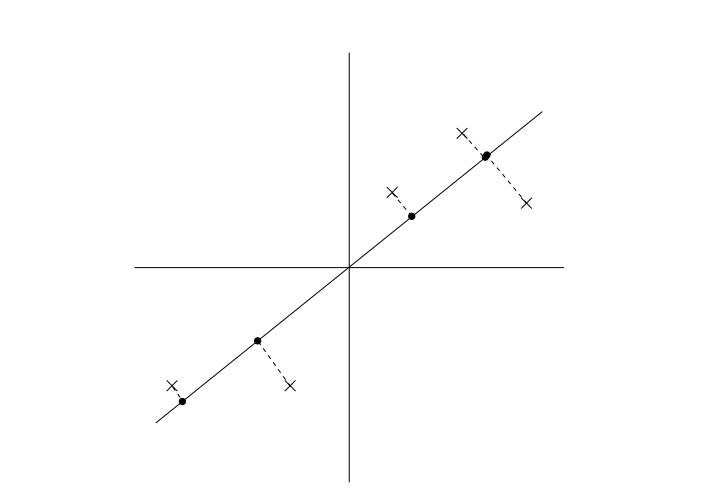
注意:与线性回归损失函数的区别
https://blog.csdn.net/weixin_43312354/article/details/10565330
多维向量降维
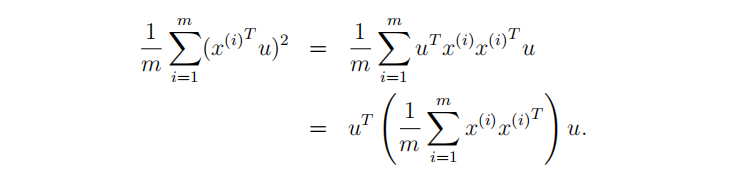
原理:线性代数–取m个n维向量的矩阵左乘其转置矩阵,得到m*m阶矩阵