
梯度下降系列博客:
- 梯度下降系列博客:1、梯度下降算法基础
- 梯度下降系列博客:2、梯度下降算法背后的数学直觉
- 梯度下降系列博客:3、批量梯度下降代码实战
- 梯度下降系列博客:4、小批量梯度下降算法代码实战
- 梯度下降系列博客:5、随机梯度下降算法代码实战
梯度下降系列的动机:
如今,可以使用众多 Python 包中的一个来实现大多数机器学习算法。我们可以在几分钟内使用这些 Python 包快速实现任何机器学习方法。然而,许多学生和专业人士在需要对算法进行更改时会遇到困难。
优化是机器学习的核心——它是使算法的结果以我们希望的方式“好”的重要组成部分。许多机器学习算法使用梯度下降算法找到其参数的最优值。因此,理解梯度下降算法对于理解 AI 如何产生好的结果至关重要。
在本系列的第一部分中,我们将提供有关梯度下降算法的内容、原因和方法的强大背景知识。在第二部分中,我们将为您提供关于梯度下降算法如何找到其参数最佳值的强大数学直觉。在本系列的最后一部分,我们将比较梯度下降算法的变体和它们在 Python 中的详尽代码示例。本系列适用于初学者和专家
什么是梯度下降算法?
维基百科正式定义短语梯度下降如下:
在数学中,梯度下降是一种用于寻找可微函数的局部最小值的一阶迭代优化算法。
梯度下降是一种机器学习算法,它迭代运行以找到其参数的最佳值。该算法在更新参数值时考虑函数的梯度、用户定义的学习率和初始参数值。
梯度下降算法背后的直觉:
让我们用一个比喻来形象化梯度下降的实际效果。假设我们正在爬山,不幸的是,在我们爬到一半的时候开始下雨了。我们的目标是尽快下山寻找避难所。那么,我们这样做的策略是什么?请记住,我们看不到很远,因为正在下雨。在我们周围的各个方向,我们只能感知到附近的动静。
这就是我想到的。我们将扫描我们周围的区域,寻找能够尽快将我们送下山的行动。一旦找到那个方向**_**,我们就会朝那个方向迈出一小步。我们将继续这样做,直到到达山脚。所以,本质上,这就是梯度下降法定位全局最小值(我们正在分析的整个数据集的最低点)的方式。以下是我们如何将这个例子与梯度下降算法联系起来。
当前位置 → → 初始参数
baby step → → → 学习率
方向 → → → 偏导数(梯度)
为什么我们需要梯度下降算法?
在许多机器学习模型中,我们的最终目标是找到最佳参数值,以降低与预测相关的成本。为此,我们首先从这些参数的随机值开始,并尝试找到最佳参数。为了找到最优值,我们使用梯度下降算法。
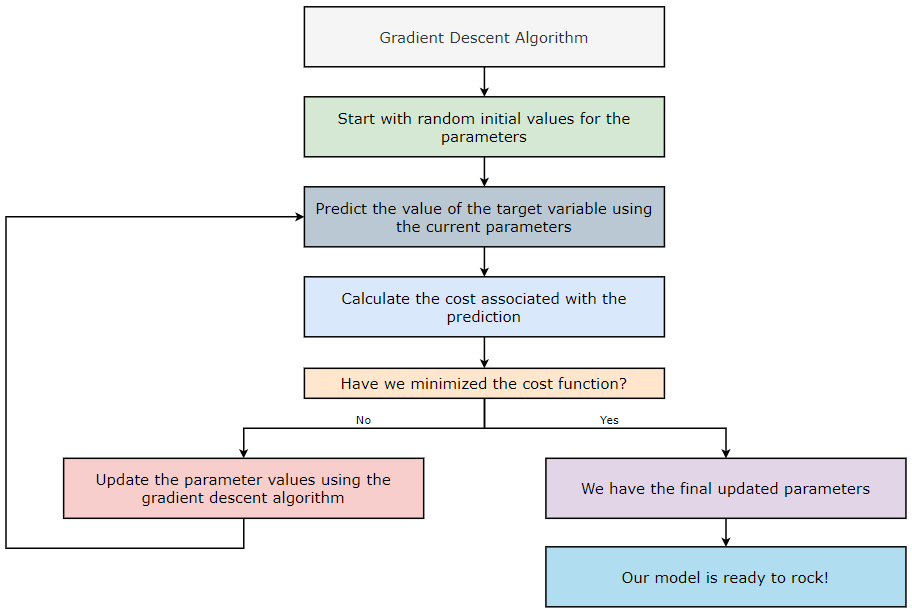
梯度下降算法如何工作?
- 从参数的随机初始值开始。
- 使用当前参数预测目标变量的值。
- 计算与预测相关的成本。
- 我们是否已将成本降至最低?如果是,则转至步骤—6。如果否,则转至步骤—5。
- 使用梯度下降算法更新参数值并返回步骤—2。
- 我们有最终更新的参数。
- 我们的模型已准备就绪(下山)!
梯度下降算法的公式:
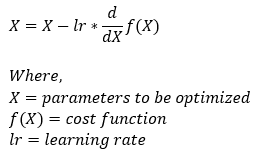
现在,让我们了解上面公式中提到的每个术语背后的含义。让我们首先从了解方向导数开始。
**注意:**我们的最终目标是尽快找到最优参数。所以,我们需要一些东西来帮助我们尽快朝着正确的方向前进。
我们为什么要使用渐变?
**梯度:**梯度不过是一个向量,其条目是函数的偏导数。
假设我们有一个变量_x的函数_f(x)_。在这种情况下,我们将只有一个偏导数。**_下图中显示的偏导数为我们提供了函数在x方向(沿_x轴)上变化(增加或减少)的速度的值。我们可以将偏导数写成梯度形式如下。
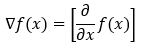
假设我们有一个包含两个变量_x_和_y的函数__f(x, y)。在这种情况下,我们将有两个偏导数。****下图中显示的偏导数为我们提供了函数在x方向和y方向(沿_x 轴和y 轴)上变化(增加或减少)的速度的值。我们可以将偏导数写成梯度形式如下。
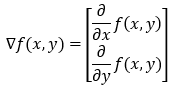
为了概括这一点,我们可以有一个带有**n 个变量的函数,它的梯度将有n 个**元素。
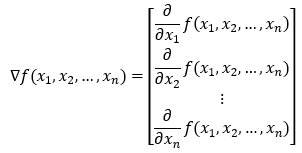
但现在的问题是,如果我们想求除沿轴以外的其他方向的导数怎么办?我们知道我们可以从一个给定的点向无限多个方向行进。现在,要找到任何方向的梯度,我们将使用方向导数的概念。
方向导数简介:
单位向量:单位向量是幅度为 1 的向量。
我们如何找到向量的长度或大小?
考虑以下向量 u。
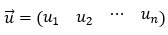
矢量的长度然后计算为其所有分量平方和的平方根。
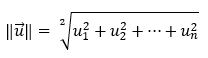
函数**f(x, y)在向量 u(单位向量)方向上的导数由函数梯度与单位向量 u的****点积**给出。在数学上,我们可以用以下形式表示它。
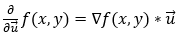
上式给出了_f(x, y)在任何方向上的偏导数。现在,让我们看看如果我们想求沿 x 轴的偏导数,它是如何工作的。首先,如果我们想求 x 方向的偏导数,单位向量 u_将为(1, 0)。现在,让我们计算沿 x轴的偏导数。
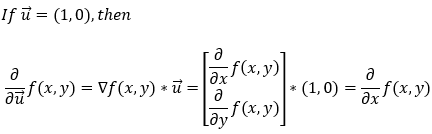
接下来,让我们看看如果我们想求沿 y 轴的偏导数,它是如何工作的。首先,如果我们想求 y 方向的偏导数,单位向量u将为(0, 1)。现在,让我们计算沿 y轴的偏导数。

**注意:**单位向量的长度(量级)必须为1。
现在我们知道如何找到所有方向的偏导数,我们需要找到偏导数给我们带来最大变化的方向,因为在我们的例子中,我们希望尽快找到最优值。
最陡的上升方向是什么?
截至目前,我们知道方向导数如下所示。
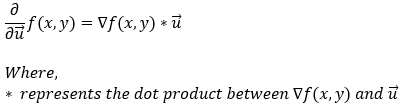
接下来,我们可以将两个向量之间的点积替换为它们之间夹角的余弦值。
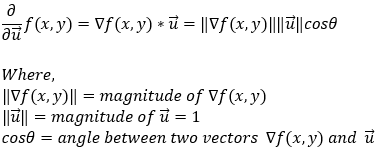
现在,请注意,由于 u 是一个单位向量,因此它的大小始终为 1。
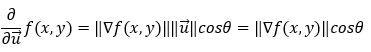
现在,在上面的等式中,我们无法控制梯度的大小。我们只能控制角度**θ。因此,为了最大化函数的偏导数,我们需要最大化cosθ**。现在,我们都知道_cosθ在_θ = 0_ ( cos0 = 1_) 时最大化 (1 )。这意味着当梯度与单位向量之间的夹角为0时,导数的值最大。换句话说,我们可以说当单位向量(方向向量)指向方向时,偏导数的值最大的渐变。
因此,总而言之,我们可以说,在梯度方向上求偏导数可以让我们得到最陡的上升。现在,让我们借助一个例子来理解这一点。
证明最陡上升方向的例子:
求函数**f(x, y) = x² + y²在点(3, 2)**处的梯度。
1. 第 1 步:
我们有两个变量**x 和 y的函数****f(x, y)**。
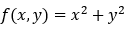
2. 第 2 步:
接下来,我们将找到函数的梯度。由于我们的函数中有两个变量,因此梯度向量将包含两个元素。
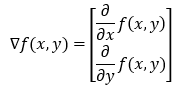
3. 第 3 步:
接下来,我们计算函数**f(x, y) = x² + y²**的梯度。
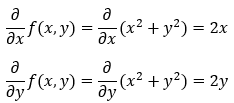
4. 第 4 步:
函数的梯度可以写成如下。
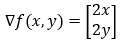
5. 第 5 步:
接下来,我们计算函数在点**(3, 2)**处的梯度。
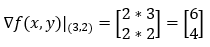
6. 第 6 步:
接下来,我们求函数**f(x, y)沿 x 轴(1, 0)**的偏导数。
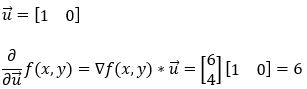
7. 第 7 步:
接下来,我们求函数 f(x, y) 沿 y 轴**(0, 1)**的偏导数。
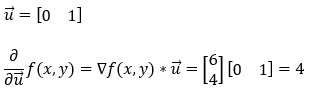
8. 第 8 步:
接下来,我们找到函数**f(x, y)在(1, 1)**方向上的偏导数。请注意,这里我们必须注意单位向量的大小。
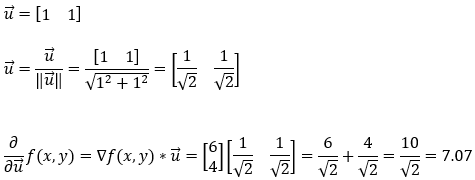
9. 第 9 步:
接下来,我们找到函数**f(x, y)在梯度(3, 2)**方向上的偏导数。请注意,这是梯度向量的方向。此外,在这里我们必须注意单位向量的大小。
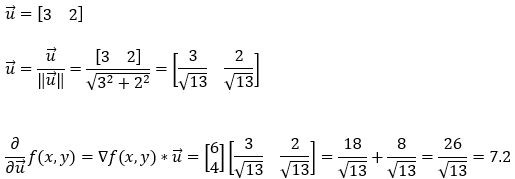
10. 第 10 步:
因此,根据 Step_6 、 Step_7 、 Step_8 、 Step_9 所示的计算,我们可以自信地说最陡**上升**的方向就是梯度的方向。
在梯度下降算法中,我们的目标是尽快找到最优参数。所以,这就是我们在梯度下降算法中使用偏导数的原因。
但是等等……有一个陷阱!
在梯度下降算法中,我们要找到最小点。然而,使用梯度会把我们带到最高点,因为它给了我们最陡峭的上升。那么,我们怎么办呢?
梯度下降算法中(—)号的解释:
现在,我们知道梯度给了我们最陡峭的上升。所以,如果我们沿着最陡峭的上升方向前进,我们将永远不会到达最低点。我们的最终目标是快速找到到达最低点的方法。因此,要朝**最陡下降方向前进,我们将沿着与最陡上升方向完全相反的方向行进。这就是我们使用(—)** 符号的原因。
为什么学习率?
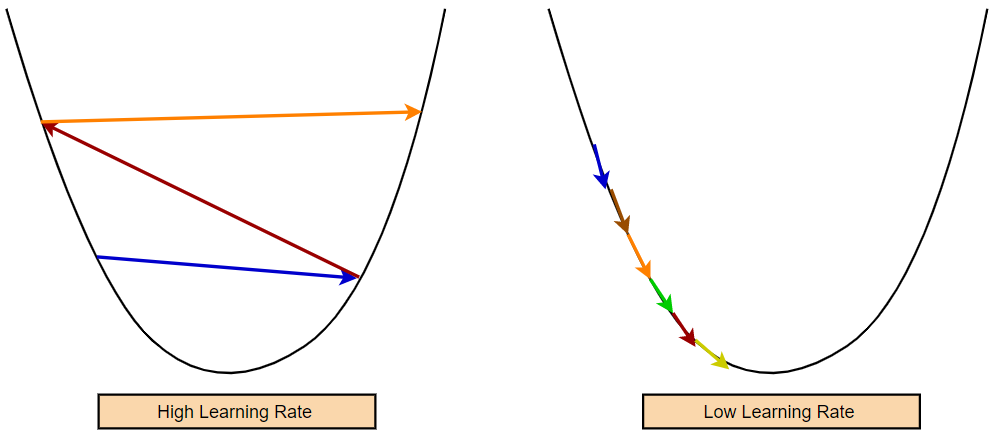
请注意,我们无法控制梯度的大小。有时我们可能会得到非常高的梯度值。因此,如果我们不以某种方式设法减缓变化的速度,我们最终将取得一些非常巨大的进步。重要的是要记住,高学习率可能只会为我们提供次优参数值。相反,较低的学习率可能需要更多的训练时期才能获得最佳值。
梯度下降法有一个超参数来调节我们的模型学习新信息的速度。这个超参数被称为学习率。我们模型的学习率决定了参数值的变化速度。我们必须将学习率设置为最佳值。如果学习率太高,我们的模型可能会迈大步而错过最小值。因此,较高的学习率可能会导致模型不收敛。另一方面,如果学习太小,模型将花费太多时间收敛。
微分的一些基本规则:
1、标量乘法规则:
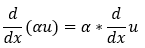
2.求和规则:
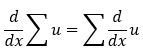
3.电源规则:

4.链式法则:

现在,让我们举几个例子来理解梯度下降算法是如何工作的。
一个变量的梯度下降:
让我们从一个非常简单的成本函数开始。假设我们有一个仅涉及一个参数_(_ θ)的成本函数( J(θ) = θ²) ,我们的目标是找到参数 ( θ ) 的最佳值,使其最小化成本函数_(_ J(θ) = θ² )。
根据我们的成本函数_(_ J(θ) = θ² _),_我们可以清楚地说它在**θ=0 时最小。**然而,当我们处理更复杂的函数时,得出这样的结论并不容易。为此,我们将使用梯度下降算法。让我们看看如何应用梯度下降算法来找到参数 ( θ ) 的最优值。
1. 第 1 步:
我们的成本函数只有一个参数 ( **θ )**由下式给出,
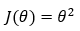
2. 第 2 步:
**我们的最终目标是通过找到参数θ**的最优值来最小化成本函数。
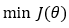
3. 第 3 步:
梯度下降算法的公式如下。

4. 第 4 步:
为了简化计算,我们考虑使用 0.1 的学习率。
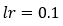
5. 第 5 步:
接下来,我们找到成本函数的偏导数。
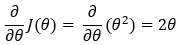
6. 第 6 步:
接下来,我们将Step_5的偏导数代入Step_3给出的公式中。
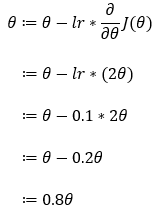
7. 第 7 步:
现在,让我们借助一个例子来了解梯度下降算法是如何工作的。在这里,我们从**θ=5 的值开始,我们将找到θ的最佳值,使成本函数最小化。接下来,我们也将从θ=-5的值开始,检查它是否可以找到成本函数的最优值。请注意,这里我们使用上面推导的梯度下降规则来更新参数θ 的值。**

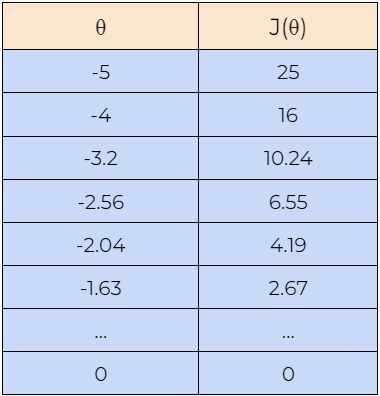
8. 第 8 步:
接下来,我们绘制上表中显示的数据图。我们可以在图中看到,梯度下降算法能够找到**θ**的最优值并最小化代价函数 J(θ)。
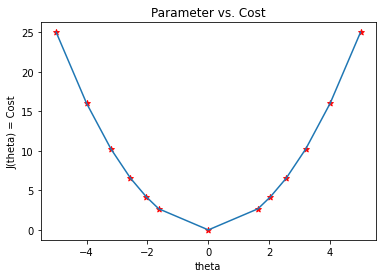
两个变量的梯度下降:
现在,让我们继续研究具有两个变量的成本函数,看看它是如何进行的。
1. 第 1 步:
**我们具有两个参数(θ1 和 θ2)**的成本函数由下式给出,
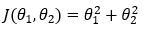
2. 第 2 步:
**我们的最终目标是通过找到参数θ1 和 θ2**的最优值来最小化代价函数。
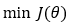
3. 第 3 步:
梯度下降算法的公式如下。

4. 第 4 步:
我们将使用步骤 3中给出的公式来找到参数**θ1 和 θ2**的最佳值。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DzkWuhXO-1675605613062)(null)]](https://img-blog.csdnimg.cn/3a5d7069305d42cc97257a68c4245d64.png)
4. 第 4 步:
接下来,我们找到成本函数关于参数**θ1 和 θ2 的偏导数。**
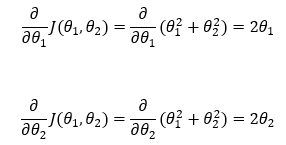
5. 第 5 步:
接下来,我们使用在步骤 — 4中导出的偏导数在步骤 — 3中进行代入。
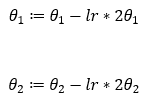
6. 第 6 步:
为了简化计算,我们将使用 0.1 的学习率。
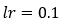
7. 第 7 步:
现在,让我们借助一个例子来了解梯度下降算法是如何工作的。在这里,我们从**θ1=1 和 θ2=1 的值开始,我们将找到θ1 和 θ2的最佳值,使成本函数最小化。接下来,我们还将从θ1=-1 和 θ2=-1**的值开始,检查梯度下降算法是否可以找到成本函数的最优值。
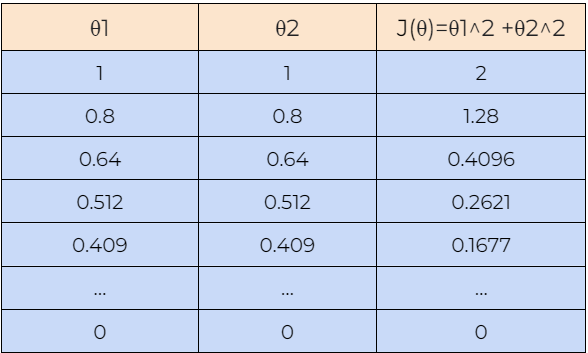
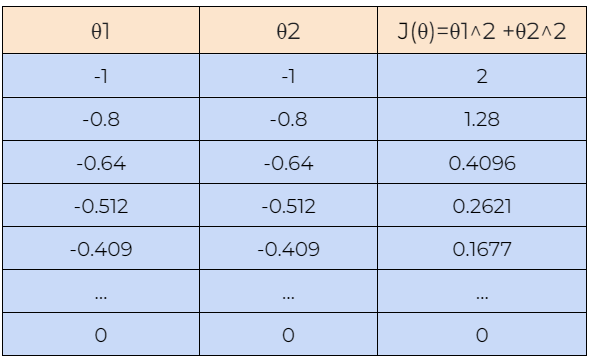
8. 第 8 步:
接下来,我们绘制上表中显示的数据图。我们可以在图中看到,梯度下降算法能够找到 θ1 和 θ2的最优值并最小化代价函数 J(θ)。
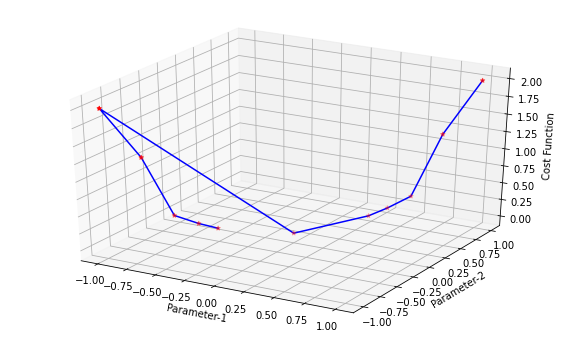
结论:
你有它!我们已经了解了梯度下降算法的基础知识及其在机器学习中的重要作用。随意复习任何第一次传递时可能不清楚的计算或概念。现在您已经成功学会了如何下山,在梯度下降系列的下一部分中了解梯度下降可以帮助解决问题的其他方法。