一、基本概念
梯度下降法,就是利用负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。梯度下降法是2范数下的最速下降法。 最速下降法的一种简单形式是:x(k+1)=x(k)-a*g(k),其中a称为学习速率,可以是较小的常数。g(k)是x(k)的梯度。
二、导数
(1)定义
设有定义域和取值都在实数域中的函数  。若
。若 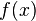 在点
在点 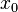 的某个邻域内有定义,则当自变量
的某个邻域内有定义,则当自变量 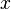 在
在 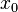 处取得增量
处取得增量 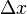 (点
(点  仍在该邻域内)时,相应地函数
仍在该邻域内)时,相应地函数  取得增量
取得增量 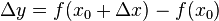 ;如果
;如果 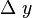 与
与 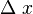 之比当
之比当  时的极限存在,则称函数
时的极限存在,则称函数  在点
在点 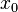 处可导,并称这个极限为函数
处可导,并称这个极限为函数  在点
在点 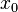 处的导数,记为
处的导数,记为 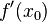 ,即:
,即:
 |
也可记作 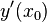 、
、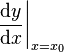 、
、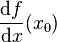 或
或  。
。
对于一般的函数,如果不使用增量的概念,函数 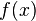 在点
在点  处的导数也可以定义为:当定义域内的变量
处的导数也可以定义为:当定义域内的变量  趋近于
趋近于  时,
时,

的极限。也就是说,
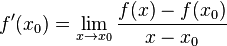
导数反应的变化率
一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数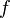 的自变量在一点
的自变量在一点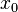 上产生一个增量
上产生一个增量 时,函数输出值的增量与自变量增量
时,函数输出值的增量与自变量增量 的比值在
的比值在 趋于0时的极限如果存在,即为
趋于0时的极限如果存在,即为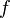 在
在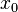 处的导数,记作
处的导数,记作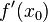 、
、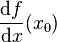 或
或
(2)几何意义:

一个实值函数的图像曲线。函数在一点的导数等于它的图像上这一点处之切线的斜率,导数是函数的局部性质。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。如果函数的自变量和取值都是实数的话,那么函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
具体来说:
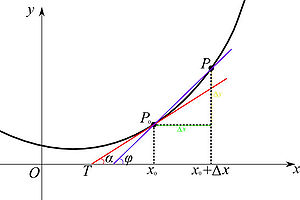
当函数定义域和取值都在实数域中的时候,导数可以表示函数的曲线上的切线斜率。如下图所示,设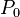 为曲线上的一个定点,
为曲线上的一个定点,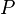 为曲线上的一个动点。当
为曲线上的一个动点。当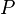 沿曲线逐渐趋向于点
沿曲线逐渐趋向于点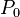 时,并且割线
时,并且割线 的极限位置
的极限位置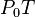 存在,则称
存在,则称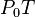 为曲线在
为曲线在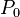 处的切线。
处的切线。
若曲线为一函数 的图像,那么割线
的图像,那么割线 (蓝色)的斜率为:
(蓝色)的斜率为:

当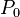 处的切线
处的切线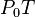 (红色),即
(红色),即 的极限位置存在时,此时
的极限位置存在时,此时 ,
,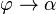 ,则
,则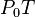 的斜率
的斜率 为:
为:

上式与一般定义中的导数定义完全相同,也就是说 ,因此,导数的几何意义即曲线
,因此,导数的几何意义即曲线 在点
在点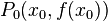 处切线的斜率
处切线的斜率
(3)导函数
导数是一个数,是指函数 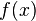 在点
在点  处导函数的函数值,若函数
处导函数的函数值,若函数  在其定义域包含的某区间
在其定义域包含的某区间  内每一个点都可导,那么也可以说函数
内每一个点都可导,那么也可以说函数 在区间
在区间  内可导,这时对于
内可导,这时对于  内每一个确定的
内每一个确定的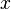 值,都对应着
值,都对应着  的一个确定的导数值,如此一来就构成了一个新的函数
的一个确定的导数值,如此一来就构成了一个新的函数 ,这个函数称作原来函数
,这个函数称作原来函数  的导函数,记作:
的导函数,记作: 、
、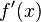 或者
或者 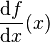 ,通常也可以说导函数为导数
,通常也可以说导函数为导数
梯度
1、相关概念
假如一个空间中的每一点的属性都可以以一个标量来代表的话,那么这个场就是一个标量场。
假如一个空间中的每一点的属性都可以以一个向量来代表的话,那么这个场就是一个向量场
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。
2、计算
一个标量函数 的梯度记为:
的梯度记为:
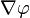 或
或 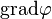
其中 (nabla)表示矢量微分算子。
(nabla)表示矢量微分算子。
在三维情况,该表达式在直角坐标中扩展为
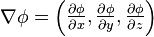
六、梯度下降法
梯度下降法,基于这样的观察:如果实值函数 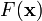 在点
在点 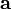 处可微且有定义,那么函数
处可微且有定义,那么函数 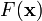 在
在 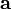 点沿着梯度相反的方向
点沿着梯度相反的方向
 下降最快。
下降最快。
因而,如果
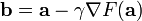
对于 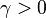 为一个够小数值时成立,那么
为一个够小数值时成立,那么 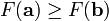 。
。
考虑到这一点,我们可以从函数  的局部极小值的初始估计
的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列 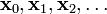 使得
使得

因此可得到
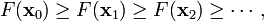
如果顺利的话序列 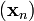 收敛到期望的极值。注意每次迭代步长
收敛到期望的极值。注意每次迭代步长 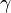 可以改变。
可以改变。