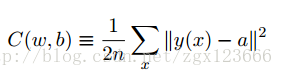前边博文说了关于MNIST手写字体的识别,现在专门记录下使用梯度下降算法进行学习的方法:
我们将⽤符号 x 来表⽰⼀个训练输⼊。为了⽅便,把每个训练输⼊ x 看作⼀个 28 *28 = 784维的向量。每个向量中的项⽬代表图像中单个像素的灰度值。我们⽤ y = y(x) 表⽰对应的期望输出,这⾥ y 是⼀个 10 维的向量。例如,如果有⼀个特定的画成 6 的训练图像,x,那么y(x) = (0,0, 0, 0, 0, 0, 1, 0, 0, 0)T 则是⽹络的期望输出。注意这⾥ T 是转置操作,把⼀个⾏向量转换成⼀个列向量。
我们希望有⼀个算法,能让我们找到权重和偏置,以⾄于⽹络的输出 y(x) 能够拟合所有的训练输⼊ x。为了量化我们如何实现这个⽬标,我们定义⼀个代价函数(也称作损失函数和目标函数):
这⾥ w 表⽰所有的⽹络中权重的集合,b 是所有的偏置,n 是训练输⼊数据的个数,a 是表⽰当输⼊为 x 时输出的向量,求和则是在总的训练输⼊ x 上进⾏的。当然,输出 a 取决于 x, w和 b,但是为了保持符号的简洁性,我没有明确地指出这种依赖关系。符号 ∥v∥ 是指向量 v 的模我们把 C 称为⼆次代价函数;有时也被称为均⽅误差或者 MSE。观察⼆次代价函数的形式我们可以看到 C(w, b) 是⾮负的,因为求和公式中的每⼀项都是⾮负的。此外,代价函数 C(w,b) 的值相当⼩,即 C(w,b) ≈0,精确地说,是当对于所有的训练输⼊ x,y(x) 接近于输出 a 时。因此如果我们的学习算法能找到合适的权重和偏置,使得 C(w,b) ≈ 0,它就能很好地⼯作。相反,当 C(w, b) 很⼤时就不怎么好了,那意味着对于⼤量地输⼊,y(x) 与输出 a 相差很⼤。因此我们的训练算法的⽬的,是最⼩化权重和偏置的代价函数 C(w, b)。换句话说,我们想要找到⼀系列能让代价尽可能⼩的权重和偏置。我们将采⽤称为梯度下降的算法来达到这个⽬的。
为什么要介绍⼆次代价呢?毕竟我们最初感兴趣的内容不是能正确分类的图像数量吗?为什么不试着直接最⼤化这个数量,⽽是去最⼩化⼀个类似⼆次代价的间接评量呢?这么做是因为在神经⽹络中,被正确分类的图像数量所关于权重和偏置的函数并不是⼀个平滑的函数。⼤多数情况下,对权重和偏置做出的微⼩变动完全不会影响被正确分类的图像的数量。这会导致我们很难去解决如何改变权重和偏置来取得改进的性能。⽽⽤⼀个类似⼆次代价的平滑代价函数则能更好地去解决如何⽤权重和偏置中的微⼩的改变来取得更好的效果。这就是为什么我们⾸先专注于最⼩化⼆次代价,只有这样,我们之后才能测试分类精度。
即使已经知道我们需要使⽤⼀个平滑的代价函数,你可能仍然想知道为什么我们在⽅程 C中选择⼆次函数。这是临时想出来的吗?是不是我们选择另⼀个不同的代价函数将会得到完全不同的最⼩化的权重和偏置呢?这种顾虑是合理的,我们后⾯会再次回到这个代价函数,并做⼀些修改。尽管如此,⽅程C中的⼆次代价函数让我们更好地理解神经⽹络中学习算法的基础,所以⽬前我们会⼀直使⽤它
重复⼀下,我们训练神经⽹络的⽬的是找到能最⼩化⼆次代价函数 C(w,b) 的权重和偏置。这是⼀个适定问题,但是现在它有很多让我们分散精⼒的结构 —— 对权重 w 和偏置 b 的解释,晦涩不清的 函数,神经⽹络结构的选择,MNIST 等等。事实证明我们可以忽略结构中⼤部分,把精⼒集中在最⼩化⽅⾯来理解它。现在我们打算忘掉所有关于代价函数的具体形式、神经⽹络的连接等等。现在让我们想象只要最⼩化⼀个给定的多元函数。我们打算使⽤⼀种被称为梯度下降的技术来解决这样的最⼩化问题。然后我们回到在神经⽹络中要最⼩化的特定函数上来。
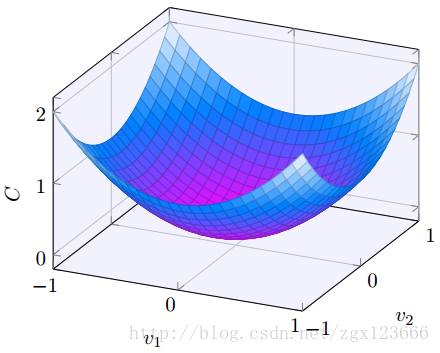
好了,假设我们要最⼩化某些函数,C(v)。它可以是任意的多元实值函数,v = v1,v2,v3...,注意我们⽤ v 代替了 w 和 b 以强调它可能是任意的函数 —— 我们现在先不局限于神经⽹络的环境。为了最⼩化 C(v),想象 C 是⼀个只有两个变量 v1 和 v2 的函数:
我们想要的是找到 C 的全局最⼩值。当然,对于上图的函数,我们⼀眼就能找到最⼩值。那只意味着,也许我展⽰的函数过于简单了!通常函数 C 可能是⼀个复杂的多元函数,看⼀下就能找到最⼩值是不可能的。
⼀种解决这个问题的⽅式是⽤微积分来解析最⼩值。我们可以计算导数去寻找 C 的极值点。运⽓好的话,C 是⼀个只有⼀个或少数⼏个变量的函数。但是变量过多的话那就是噩梦。⽽且神经⽹络中我们经常需要⼤量的变量——最⼤的神经⽹络有依赖数亿权重和偏置的代价函数,极其复杂。⽤微积分来计算最⼩值已经不可⾏了。(确定我们将可以通过有两个变量的函数 C 来理解神经⽹络后,我已经两次提到:“嘿,如果函数有远多于两个变量怎么办?”。对此我只能说很抱歉。请相信我把 C 想象成⼀个⼆元函数是有助于我们的理解的。有时候这种想象的画⾯会遇到障碍,这正是上⾯两个段落在帮助你克服的。善于思考数学通常也涉及到有效地利⽤多种直觉上的想象画⾯,学会什么时候⽤什么画⾯合适。)
好吧,微积分是不能⽤了。幸运的是,有⼀个漂亮的推导法暗⽰有⼀种算法能得到很好的效果。⾸先把我们的函数想象成⼀个⼭⾕。只要瞄⼀眼上⾯的绘图就不难理解。我们想象有⼀个⼩球从⼭⾕的斜坡滚落下来。我们的⽇常经验告诉我们这个球最终会滚到⾕底。也许我们可以⽤这⼀想法来找到函数的最⼩值?我们会为⼀个(假想的)球体随机选择⼀个起始位置,然后模拟球体滚落到⾕底的运动。我们可以通过计算 C 的导数(或者⼆阶导数)来简单模拟——这些导数会告诉我们⼭⾕中局部“形状”的⼀切,由此知道我们的球将怎样滚动。
看到这⾥你可能会以为我们会写下球体的⽜顿运动定理,考虑摩擦⼒、重⼒等影响。实际上,我们不打算真的去实现这个球体滚落的推导 —— 我们是在设计⼀个最⼩化 C 的算法,⽽不是在⽤物理定律做精确的仿真。对球体的⾁眼观察是为了激发我们的想象⽽不是束缚我们的思维。因此与其陷进物理学⾥凌乱的细节,不如我们就这样问⾃⼰:如果我们扮演⼀天的上帝,能够构造⾃⼰的物理定律,能够⽀配球体可以如何滚动,那么我们将会采取什么样的运动学定律来让球体能够总是滚落到⾕底呢?
为了更精确地描述这个问题,让我们思考⼀下,当我们在 v1 和 v2 ⽅向分别将球体移动⼀个很⼩的量,即 ∆v1 和 ∆v2 时,球体将会发⽣什么情况。微积分告诉我们 C 将会有如下变化:
我们要寻找⼀种选择 ∆v1 和 ∆v2 的⽅法使得 ∆C 为负;即,我们选择它们是为了让球体滚落。为了弄明⽩如何选择,需要定义 ∆v 为 v 变化的向量,∆v (∆v1,∆v2)T,T 是转置符号
我们也定义 C 的梯度为偏导数的向量。
我们⽤ ∇C 来表⽰梯度向量,即:
我们⻢上会⽤ ∆v 和梯度 ∇C 来重写 ∆C 的变化。在这之前我想先澄清⼀些令⼈困惑的关于梯度的事情。当第⼀次碰到 ∇C 这个符号,⼈们有时会想知道怎么去理解 ∇ 符号。∇ 究竟是什么意思?事实上你可以把 ∇C 仅仅看做⼀个简单的数学记号 —— 上⾯定义的向量 —— 这样就不必写两个符号了。这样来看,∇ 仅仅是⼀个符号,犹如⻛中摆动的旗帜,告诉你:“嘿,∇C 是
⼀个梯度向量”。也有很多其它的数学上不同视⻆对于 ∇ 的专业解释(⽐如,作为⼀个微分操作),但我们不需要这些观点。
有了这些定义,∆C 的表达式 (7) 可以被重写为:
∆C ≈∇C * ∆v
注意具有这⼀规则的梯度下降并不是模仿实际的物理运动。在现实中⼀个球体有动量,使得