简介
PCA是一种针对连续变量的降维算法,它的根本目的就是选取能够最大化解释数据变异的成分,将数据从高维降到低维,同时保证各个维度之间正交(无相关性)。
一句话解释版本:
PCA是一种降维方法,它能把很多个自变量转换成少许相互不相关的新自变量,从而在保证数据变化被抓取的前提下减少自变量个数并消除自变量间相关性。
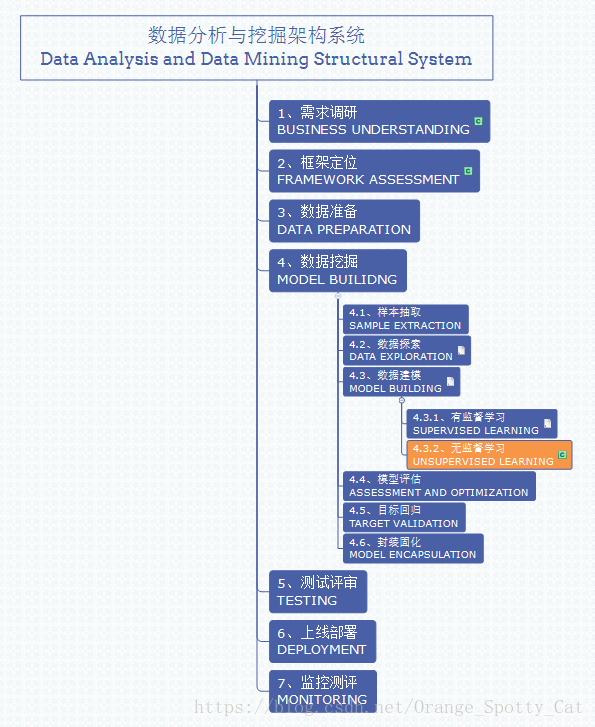
数据分析与挖掘体系位置
主成分分析不是一种预测模型,它是数据降维的方法。此外,PCA并没有一个预测主体,因此属于无监督学习。
在无监督学习中,常见的方法有如下三种:
- 降维分析
- 聚类分析
- 关联分析
本篇主要介绍降维分析中的主成分分析方法,即PCA。
此方法在整个数据分析与挖掘体系中的位置如下图所示。
主成分分析的定义
主成分分析简称PCA,英文全称Principal Component Analysis。它是无监督学习中降维模型中的一类,在实际的数据探索与建模中应用十分广泛。上面的说法较为晦涩,如果把上面的话说的平民化一些,就是:PCA能够从旧的相互可能相关的自变量中衍生出新的互不相关的自变量,从而减少自变量的个数,同时又能保证数据的变化被大幅度的解释。
主成分分析的理解与计算
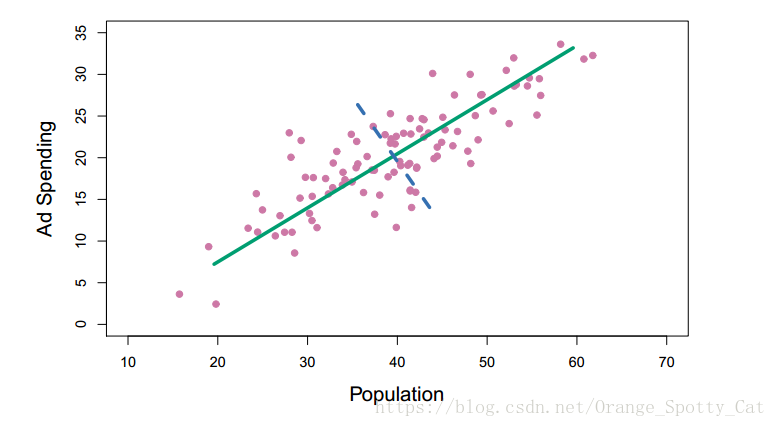
主成分分析的具体方法是对变量的协方差矩阵(Co-variance Matrix)或相关系数矩阵(Correlation Matrix)求取特征值和特征向量。经证明,对应最大特征值的特征向量,其方向正是协方差矩阵变异最大的方向,依次类推,第二大特征值对应的特征向量,是与第一个特征向量正交且能最大程度解释数据剩余变异的方向,而每个特征值则能够衡量各方向上变异的程度。因此,进行主成分分析时,选取最大的几个特征值对应的特征向量,并将数据映射在这几个特征向量组成的参考系中,达到降维的目的(选择的特征向量数量低于原始数据的维数)。上图显示的是人口量(Population)与广告投入金额(Ad Spending)的散点图。图中绿色的线就代表着PCA中的第一个主成分。从图上能明显的看出来,绿色直线所在的区域是粉色点变化性(Variability)是最高的区域(数据最容易在绿线上变动),也就是说,绿色的直线是离图上所有粉色点(Observations)最近的一条线。这说明,如果把图上所有粉色的点投射到线上,计算所有点到绿线的距离后并加总,得到的结果数值是最小的。投射到其他任意直线得到的结果都要比投射在绿线产生的结果大。
因此,这条绿线就是PCA要寻找到的第一个主成分,第一主成分,也被称为第一主成分向量(the First Principal Component Vector)。它代表着那条离所有观测值最近的直线。各个观测值到这条直线的垂直距离平方和是最小的。
通过把人口(pop)与广告投入(Ad)两个变量降低到一条直线代表的数值,我们就实现了数据的降维。从二维到一维。
下面,我们需要用数学的形式将这条绿色的线表示出来,经过计算,绿色线的公式为:
Zi1 = 0.839 × (pop - avg(pop)) + 0.544 × (ad - avg(ad))
其中,φ1 = 0.839 , φ2 = 0.544。φ1 与φ2分别是主成分载荷(Principal Component Loadings),它们定义了绿色线的倾斜度。avg(pop)与avg(ad)分别代表横轴与纵轴上观测值的平均值。
用这种方法,我们就能通过pop与ad的值来直接计算Zi1 的值。Zi1被我们称为主成分分值(Principal Component Score),它可以被看作一个衍生变量值,Z值能够同时最大程度上反应pop与ad的取值情况。这也就是说,第一主成分能在最大程度上抓取所有变量的信息。
举例来说,如果Zi1 = 0.839 × (pop - avg(pop)) + 0.544 × (ad - avg(ad)) < 0,就表示一个低于平均人口并且低于平均广告消费的观测值。每一个pop与ad的值都能计算出一个对应的Zi1 值。由此,我们就实现了数据从二维(pop;ad)到一维(Zi1)的转换。
我们在前面着重讨论了第一主成分,在PCA中,有多少的维度,就可以有多少个主成分。第一主成分能在最大范围内解释数据的变化。那么如果有第二个成分,它与第一主成分正交,那么可以说,第二个成分中肯定含有第一主成分完全没有包含的变化。以此类推,有多少个变量,就最多可以产出多少个成分。
但是PCA的模型限制了第一主成分能最大程度解释观测值的变化,之后是第二、第三,...,以此类推。
主成分分析的应用
PCA主要应用在三个方面:
1.降维并对数据进行描述
以上面的例子解释,我们通过Z的值,可以同时解释人口与广告消费这两个自变量的状态。当实际生活中,数据维度众多时,可以通过一两个结果反映并描述大多数据的情况。
2. 对数据做综合打分
假设我们想用人口与广告消费情况两个因素来解释一个城市的发展程度,并给这个城市一个整体评分时。我们可以直接通过公式计算第一主成分的值,用Z-Score当作城市发展的评分。Z-Score越高,我们的城市发展水平越高。这样我们就避免了需要同时分析多维度数据。
3. 为回归聚类模型引入无相关性自变量
通过PCA分析得到的所有主成分都是相互独立的,这是因为各个主成分之间都符合正交公式。因此,用主成分替代原有的自变量可以在本质上消除自变量之间的相关性。
在线性回归中,重要假设之一就是自变量之间的相互独立性,PCA直接满足了这一假设。
同时,多自变量会引发高维度问题,PCA在保证数据可解释的前提下,又能减少自变量的个数。
主成分分析在R中的实现
主成分分析可以直接用R自带的prcmp()公式计算。
下面是用R实现PCA的实例,注意,PCA适用于数值型连续数据,使用前需要将数据进行标准化处理。
states <- row.names(USArrests) # 引入R自带的数据作为样本数据 states # 进行PCA处理,生成所有主成分结果 # scale = TRUE代表我们要对数据进行标准化处理。这是使用PCA的推荐处理。 # 默认情况下,prcomp()会将自变量标准到均值为0,scale=TRUE条件会将数据被标准化到std=1 pr.out <- prcomp(USArrests, scale = TRUE) # 展示PCA的结果 names(pr.out) summary(pr.out) # 给出principal component loadings pr.out$rotation # 通过散点图展示第一主成分与第二主成分plot the biplot (pr.out , scale =0)