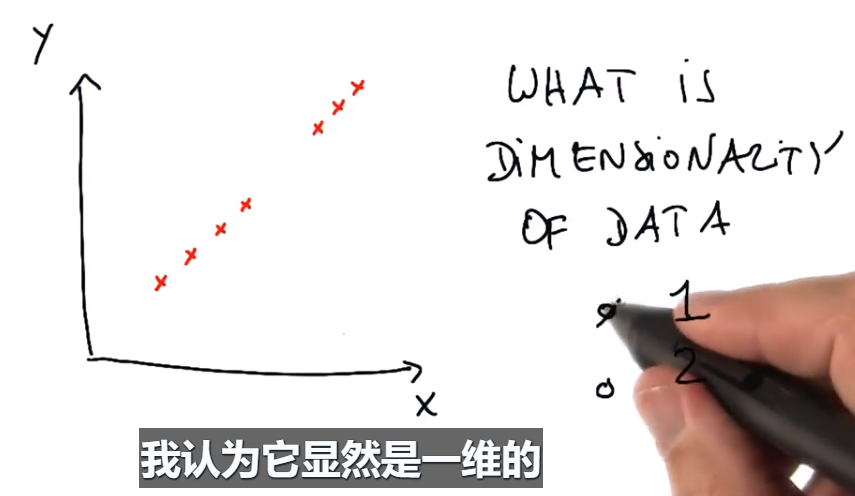
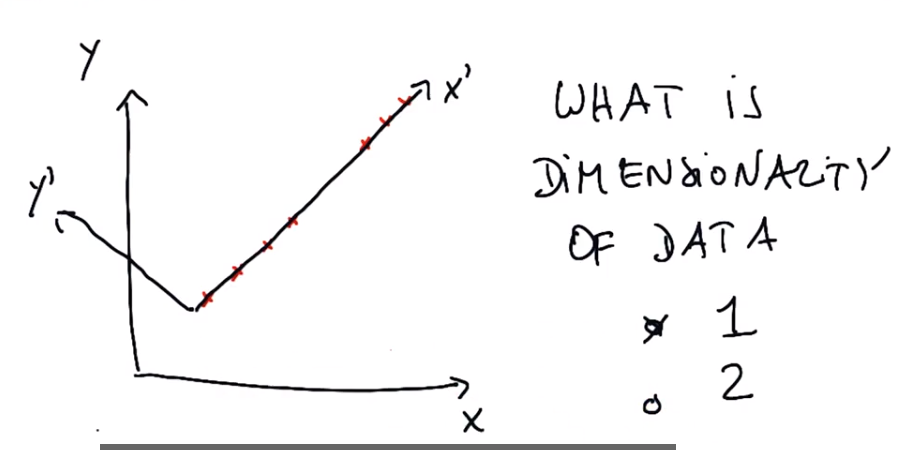
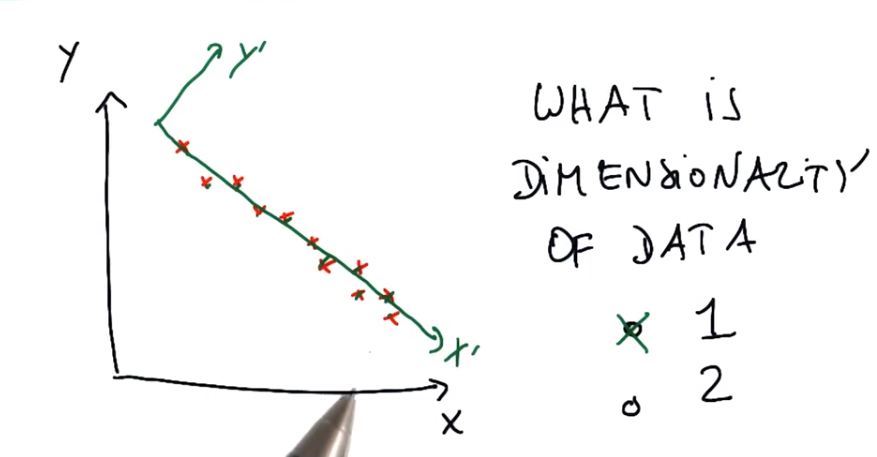
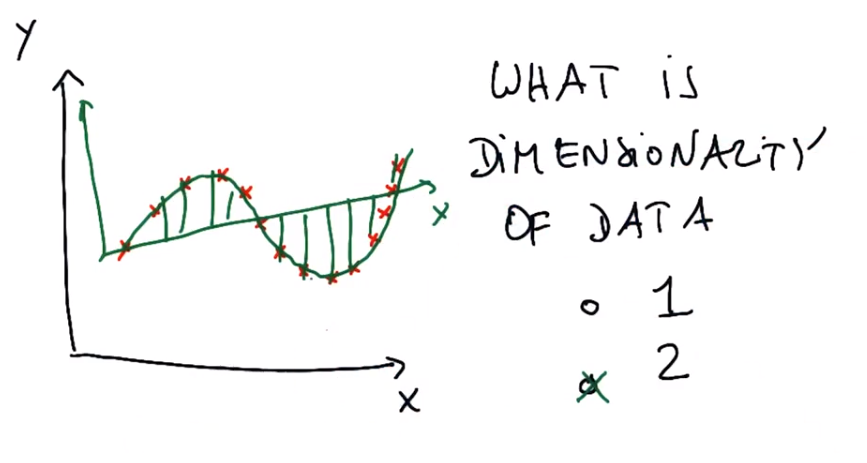
以下数据是一维还是二维
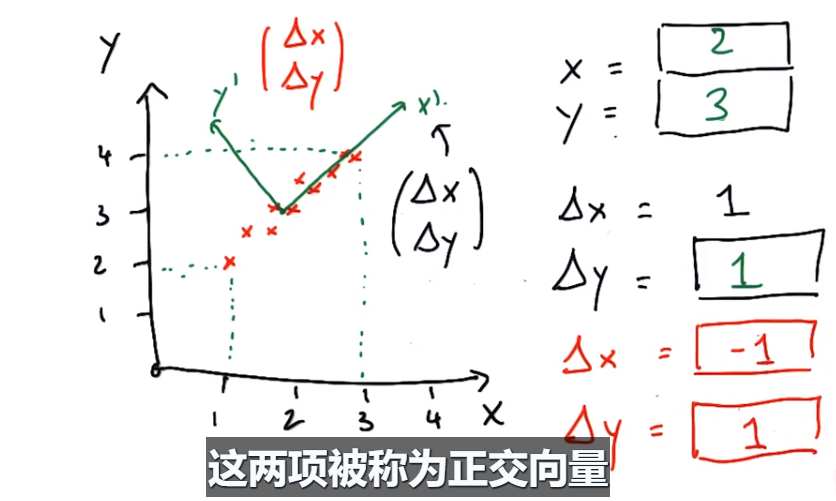
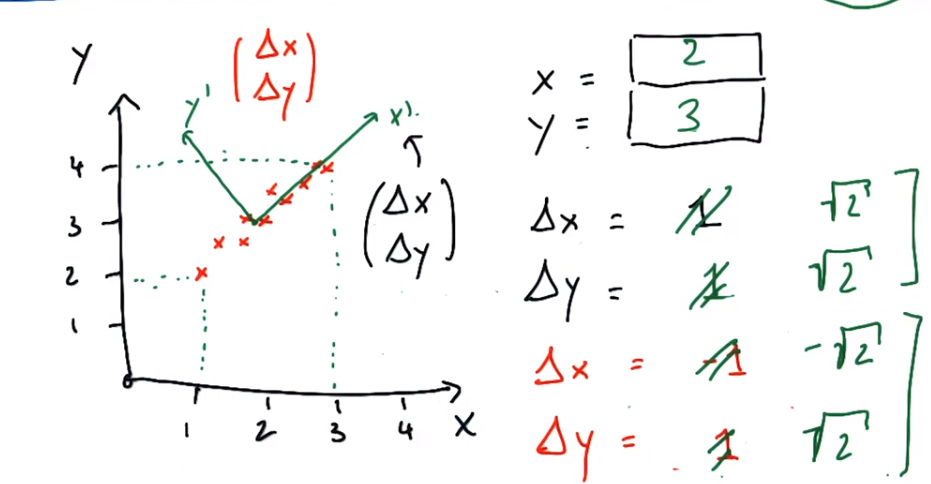
练习1:通过PCA找到新坐标系的中心(2,3),△x=1,沿坐标系x’向右移,则△y=1;△y=1,沿坐标系y’向上移,则△x=-1
向量长度√2,按原坐标系计算
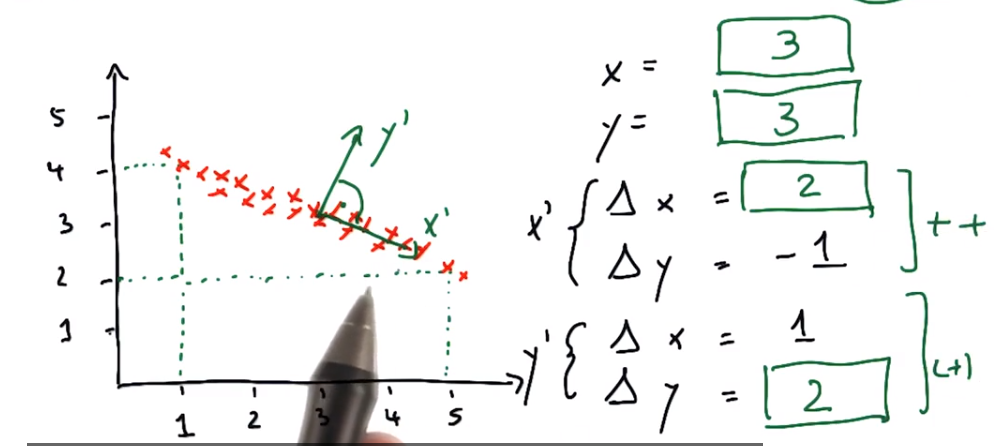
练习2:通过PCA找到新坐标系的中心(3,3),△y=-1,沿坐标系x’移动,则△x=2;△x=1沿坐标系y’移动,则△y=2
x’=0.5a+3.5
x’+△y=0.5(a+△x)+3.5
因为△y=1,则△x=2
y’=2a-3(两直线垂直斜率乘积-1)
y’+△y=2(a+△x)-3
因为△x=1,则△y=2
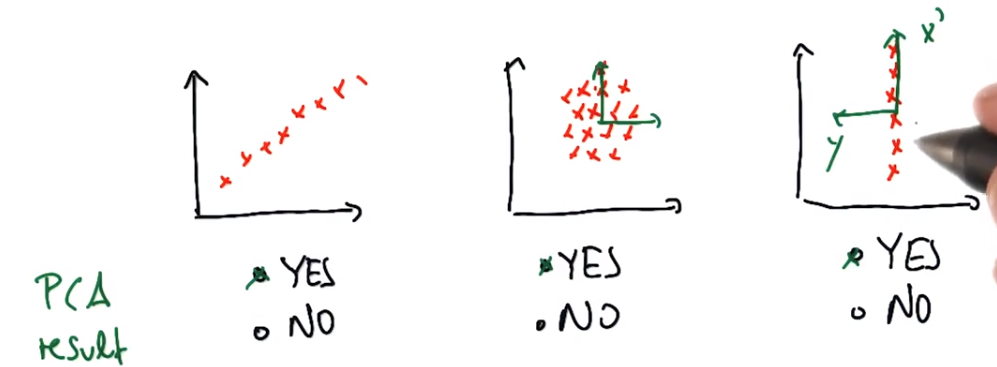
练习:哪些数据可以用于PCA?
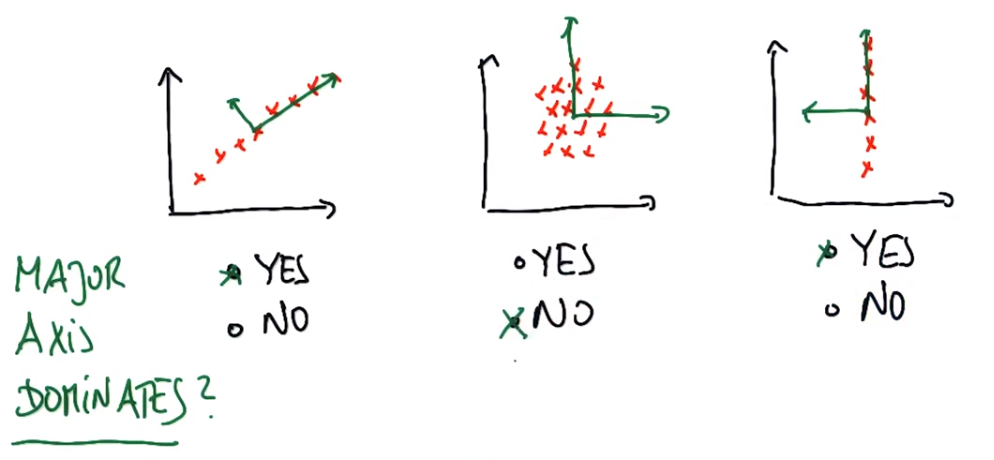
练习:轴何时占主导地位
长轴是否占优势(长轴特征值远远大于短轴特征值)?1和3长轴捕获了全部数据,2中短轴与长轴不断延伸,因此其两个特征值可能具有相同的量级,而我们实际上并没有通过运行pca获得更多信息
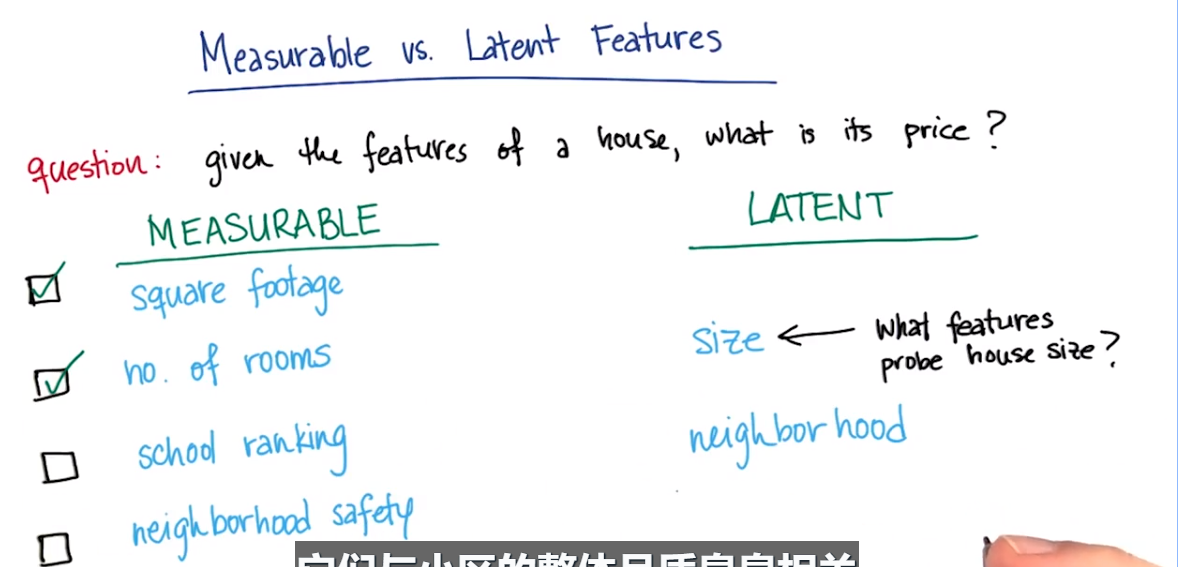
从四个特征到两个
在不知道有多少特征的情况下,选择size和neighborhood特征,用SelectKBest(只保留K个最适合特征)
SelectPercentile(保留的特征的百分比)
复合特征:
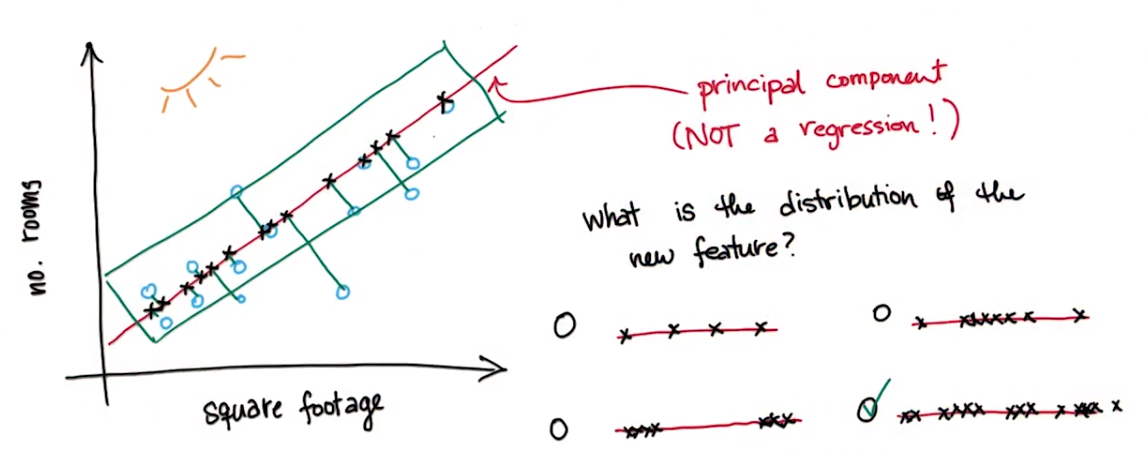
二维特征通过映射成一维
练习:沿着最大方差的维度进行映射时,能够保留原始数据中最多的信息
练习:最大主成分数量=训练点数量和特征数量的最小值
PCA回顾/定义:
1.PCA是将输入特征转换为其主成分的系统化方式,这些主成分之后可供你使用,而非原始输入特征,你将其用作回归或分类任务中的新特征。
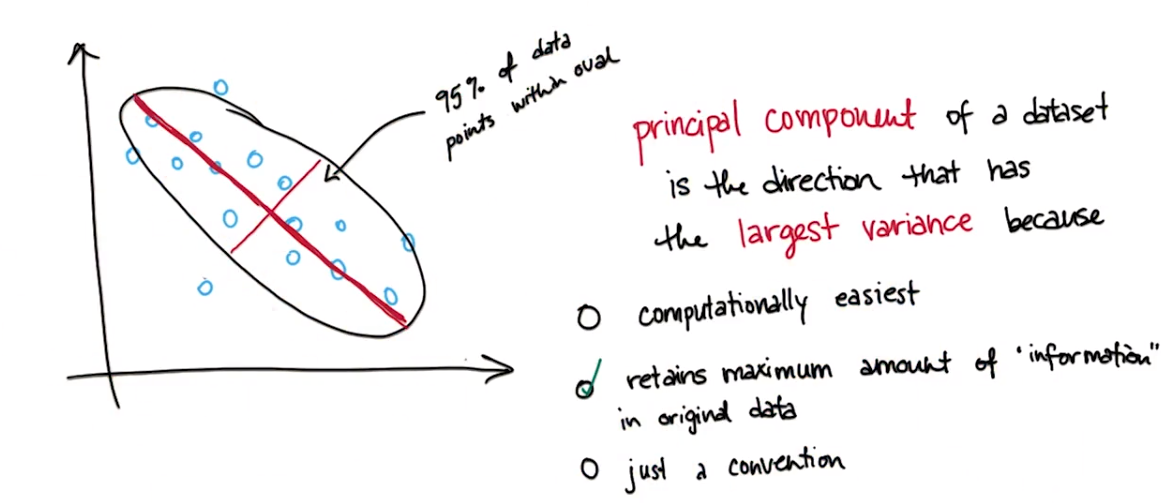
2.主成分的定义是数据中会使方差最大化的方向,它可以在你对这些主成分执行投影或压缩时将出现信息丢失的可能性降至最低,
3.你还可以对主成分划分等级,数据因特定主成分而产生的方差越大,那么该主成分的级别越高,因此产生方差最大的主成分即为第一个主成分,产生方差第二大的则为第二个主成分,以此类推。
4.主成分在某种意义上是相互垂直的,因此从数学角度出发,第二个主成分绝不会与第一个主成分重叠,第三个也不会通过第二个与第一个重叠等,因此,在某种意义上你可以将它们当作单独的特征对待
5.主成分数量有上限=数据集中的输入特征数量
何时使用PCA:
1.如果你想要访问隐藏的特征,而你认为这些特征可能显示在你的数据的图案中,你要尝试做的所有工作可能就是确定是否存在隐藏的特征,换句话说,你只是想知道第一个主成分的大小(示例:是否可以估量出Enron的大亨是谁)
2.降维的三种使用情况
——可视化高维数据(如何在只有两个维度的情况下画出能够表示数据点的三个、四个或更多特征,将其投射到前两个主成分,然后只要标绘并画出散点图)
——怀疑数据中存在噪音的情况,几乎所有数据中都存在噪音,希望第一个或第二个是你最强大的主成分捕获数据中的真正的模式,而较小的主成分只表示这些模式的噪音变体,因此通过抛弃重要性较低的主成分去除这些噪音
——在使用另一个算法前使用PCA进行预处理,即归纳或分类任务,如果你有很高的维数,且算法复杂度很高,那么算法的方差会很高,最终会被数据中的噪音同化(特征脸,将PCA用于人的照片的方法,照片中有许多像素,如果你要识别图片中拍摄的人的身份,运行某种人脸识别或识别照片内容,使用PCA可以将非常搞得输入维数降低至可能 其原来的十分之一,将其填入SVM然后进行真正的识别)
sklearn中的PCA
>>> import numpy as np >>> from sklearn.decomposition import PCA >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> pca = PCA(n_components=2) >>> pca.fit(X) PCA(copy=True, iterated_power='auto', n_components=2, random_state=None, svd_solver='auto', tol=0.0, whiten=False) >>> print(pca.explained_variance_ratio_) [ 0.99244... 0.00755...] >>> print(pca.singular_values_) [ 6.30061... 0.54980...]
PCA迷你项目:
练习:我们提到 PCA 会对主成分进行排序,第一个主成分具有最大方差,第二个主成分 具有第二大方差,依此类推。第一个主成分可以解释多少方差?0.19346534 第二个呢?0.15116844
方差比(是特征值得具体表现形式):
print pca.explained_variance_ratio_#可释方差
练习:现在你将尝试保留不同数量的主成分。在类似这样的多类分类问题中(要应用两个以上标签),准确性这个指标不像在两个类的情形中那么直观。相反,更常用的指标是 F1 分数。
我们将在评估指标课程中学习 F1 分数,但你自己要弄清楚好的分类器的特点是具有高 F1 分数还是低 F1 分数。你将通过改变主成分数量并观察 F1 分数如何相应地变化来确定。
将更多主成分添加为特征以便训练分类器时,你是希望它的性能更好还是更差?
could go either way
While ideally, adding components should provide us additional signal to improve our performance, it is possible that we end up at a complexity where we overfit.
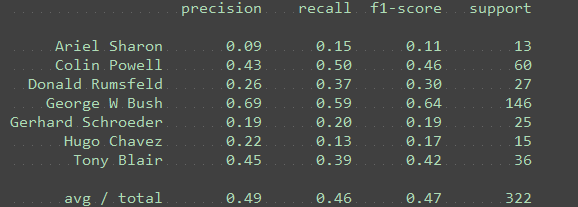
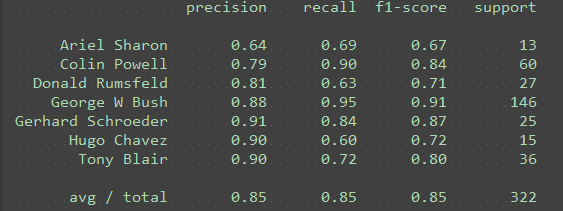
练习:将 n_components 更改为以下值:[10, 15, 25, 50, 100, 250]。对于每个主成分,请注意 Ariel Sharon 的 F1 分数。(对于 10 个主成分,代码中的绘制功能将会失效,但你应该能够看到 F1 分数。)
如果看到较高的 F1 分数,这意味着分类器的表现是更好还是更差? better
n_components =10
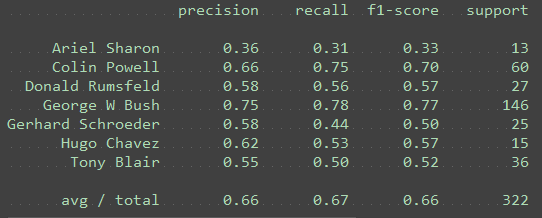
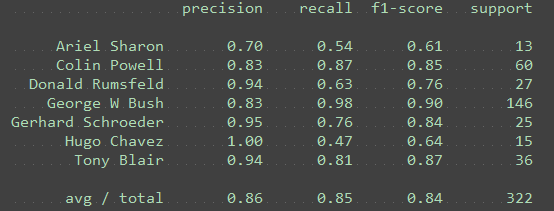
n_components = 15
n_components = 25
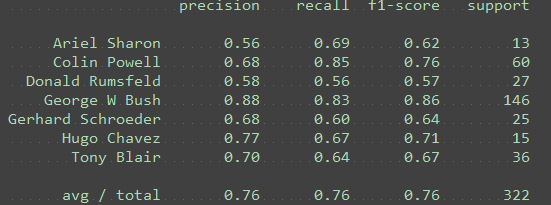
n_components = 50
n_components = 100
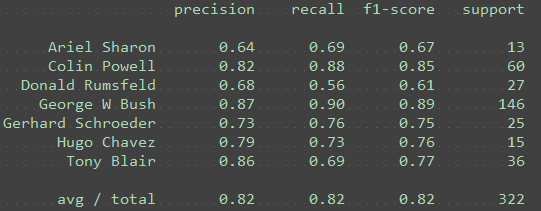
n_components = 150
n_components = 250
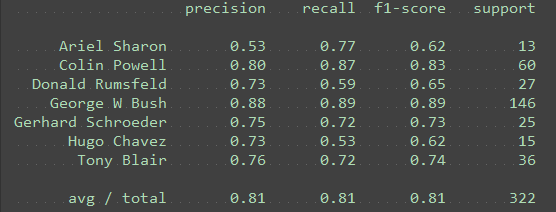
练习:在使用大量主成分时,是否看到过拟合的任何证据?PCA 维度降低是否有助于提高性能?
是,PC 较多时性能会下降,当250个特征的时候明显比100的下降了
练习:选择主成分
主要的方法就是尝试,直到到某一点时增加会导致下降或者不动,那说明到头了
针对不同的主要成分数量进行训练,然后观察,对于每一个可能的主要成分数量,算法的查准率如何,重复几次后发现,在某一个点上会出现收益递减的情况,即在添加更多的主要成分后结果没有太多差异