机器学习十大算法——主成分分析 PCA(principal components analysis)
降维
宇宙,是时间和空间的总和。时间是一维的,而空间的维度,众说纷纭,至今没有定论。弦理论说是9维,霍金所认同M理论则认为是10维。它们解释说人类所能感知的三维以外的维度都被卷曲在了很小的空间尺度内。当然,谈及这些并不是为了推销《三体》系列读物,更不是引导读者探索宇宙真谛,甚至怀疑人生本质,而是为了引出今天机器学习课堂主题——降维。
机器学习中的数据维数与现实世界的空间维度本同末离。在机器学习中,数据通常需要被表示成向量形式以输入模型进行训练。但众所周知,对高维向量进行处理和分析时,会极大消耗系统资源,甚至产生维度灾难。例如在CV(计算机视觉)领域中将一幅100x100的RGB图像提取像素特征,维度将达到30000;在NLP(自然语言处理)领域中建立<文档-词>特征矩阵,也动辄产生几万维的特征向量。因此,进行降维,即用一个低维度的向量表示原始高维度的特征就显得尤为重要。试想,如果宇宙真如M理论所说,每个天体的位置都由一个十维坐标来描述,应该没有一个正常人能想象出其中的空间构造。但当我们把这些星球投影到一个二维平面,整个宇宙便会像上面的银河系一样直观起来。
常见的降维方法主要有主成分分析(PCA)、线性判别分析(LDA)、等距映射(Isomap)、局部线性嵌入(LLE)、拉普拉斯特征映射(LE)、局部保留投影(LPP)等。这些方法又可以按照线性/非线性,监督/非监督,全局/局部,进行不同划分。其中 PCA作为最经典的方法,至今已有100多年的历史,它属于一种线性、非监督、全局的降维算法。我们今天就来回顾一下这经久不衰的百年经典。
主成分分析属于统计学的方法,过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
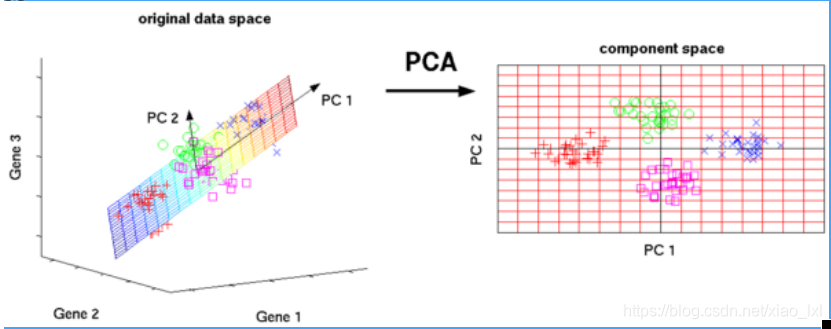
主成分分析的一些实际应用包括数据压缩,简化数据表示,数据可视化等。值得一提的是需要领域知识来判断是否适合使用主成分分析算法。如果数据的噪声太大(即各个成分的方差都很大),就不适合使用主成分分析算法。
PCA 算法
PCA的原理及目标函数
PCA(principal components analysis), 即主成分分析,旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x, y, z这三个轴来表示数据,需要使用三个维度,而实际上这些点只出现在一个二维平面上,如果我们通过坐标系旋转使得数据所在平面与x, y平面重合,那么我们就可以通过x’, y’两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维,而x’, y’两个轴所包含的信息就是我们要找到的主成分。
但在高维空间中,我们往往不能像刚才这样直观地想象出数据的分布形式,也就更难精确地找到主成分对应的轴是哪些。不妨,我们先从最简单的二维数据来看看PCA究竟是如何工作的。
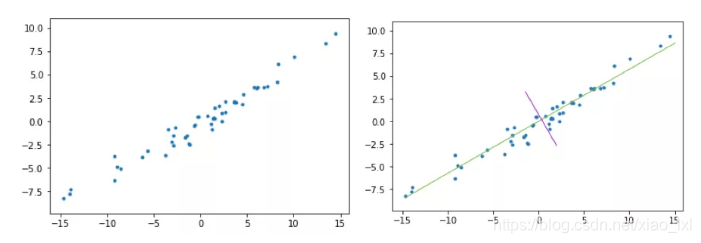
上图(左)是二维空间中经过中心化的一组数据,我们很容易看出主成分所在的轴(以下称为主轴)的大致方向,即右图中绿线所处的轴。因为在绿线所处的轴上,数据分布的更为分散,这也意味着数据在这个方向上方差更大。在信号处理领域中我们认为信号具有较大方差,噪声具有较小方差,信号与噪声之比称为信噪比,信噪比越大意味着数据的质量越好。由此我们不难引出PCA的目标,即最大化投影方差,也就是让数据在主轴上投影的方差最大。


PCA的求解方法
熟悉线性代数的读者马上就会发现,原来,x投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值,最佳投影方向就是最大特征值所对应特征向量。次佳投影方向位于最佳投影方向的正交空间中,是第二大特征值对应的特征向量,以此类推。至此,我们得到了PCA的求解方法:


PCA 最小平方误差理论
问题描述
观察到其实PCA求解的是最佳投影方向,即一条直线,这与数学中线性回归问题的目标不谋而合,能否从回归的角度定义PCA的目标并相应地求解问题呢?
分析
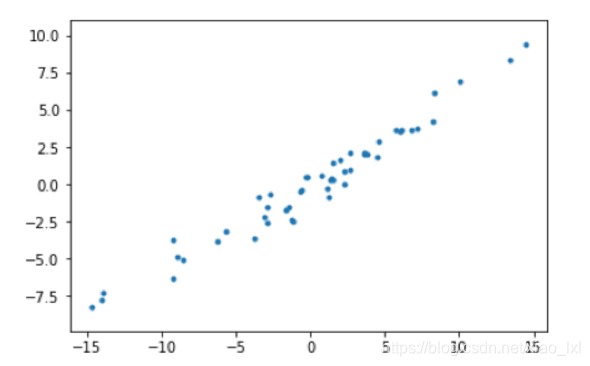
我们还是考虑二维空间这些样本点,最大方差角度求解的是一条直线,使得样本点投影到这条直线上的方差最大。从求解直线的思路出发,很容易联想到数学中的线性回归问题,其目标也是求解一个线性函数使得对应直线能够更好地拟合样本点集合。如果我们从这个角度定义PCA的目标,那么问题就会转化为一个回归问题。
顺着这个思路,在高维空间中,我们实际上是要找到一个d维超平面,使得数据点到这个超平面的距离平方和最小。对于一维的情况,超平面退化为直线,即把样本点投影到最佳直线,最小化的就是所有点到直线的距离平方之和,如下图所示。
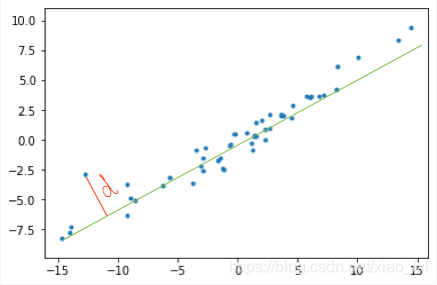



第一项xkTxk与我们选取的W无关,是个常数。我们利用刚才求出的投影向量表示将第二项和第三项分别继续展开
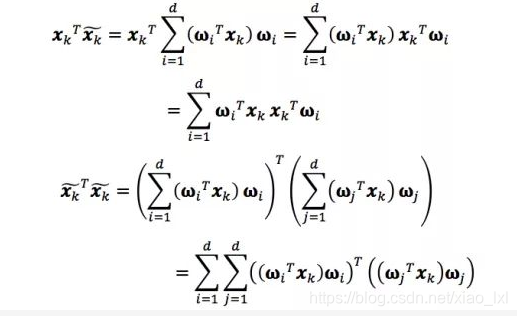
其中ωiTxk和ωjTxk表示投影长度,都是数字。且i≠j时,ωiTωj=0,因此上式的交叉项中只剩下d项。

我们要最小化的式子即对所有的k求和,可以写成

如果我们对W中的d个基ω1, ω2, …, ωd依次求解,就会发现和上一节中方法完全等价。比如当d=1时,我们实际求解的问题是
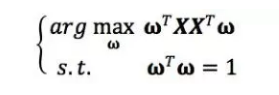
这个最佳直线ω与最大方差法求解的最佳投影方向一致,即协方差矩阵的最大特征值所对应的特征向量,差别仅是协方差矩阵∑的一个倍数,以及一个常数偏差,但这并不影响我们对最大值的优化。