数据压缩_任务二_主成分分析PCA

作业2：
主成分分析：步骤、应用及代码实现

一、 什么是PCA？

1、PCA介绍

在减少需要分析的指标同时，尽量减少原指标包含信息的损失，已达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系，因此有可能用较少的综合指标分别综合各变量中的各类信息。核心要点在于舍弃权重较低的特征或者信息。

2、PCA应用

PCA主要用于数据降维，在一个图像矩阵中，有些元素特征不明显，不能用来做识别，而有些元素特征很明显，表现在方差很大(某个元素的方差可以度量其相对于整个样本的离散性)，这些元素常常作为图像识别的依据。PCA的作用就是去除那些方差较小，特征不明显的维，保留方差较大，有利于识别的维。这样降低了图像矩阵的维数，减小了运算量。
参考文档

3、数据降维

参考《线性代数》：通过数据中心化和旋转坐标系，一般来讲n维空间中的n个点一定能在一个n-1维子空间中分析。

以三维空间举例，尽管上述操作将3维数据降成2维，但数据降维后并没有丢失任何信息，因为这些数据在第3个维度的分量都为0。
此时，假设数据在z’轴有一个微小的抖动，我们仍可以用上述的二维表示这些数据，原因是我们可以认为x’、y’轴的信息是数据的主成分，z’上的抖动可能是噪声。
换言之，本来这组数据是有相关性的，噪声的引入导致了数据的不完全相关，但是这些数据在z’轴的分布与原点构成的夹角非常小，在z’轴上具有很大的相关性，综合考虑，就可以认为数据在x’、y’上的投影构成了数据的主成分。

PCA的思想就是将n维特征映射到k维上（k<n），这k维数全新的正交特征，称为主成分。

需要注意的是：
1、新的k维是重新构造的，而非简单的从n维特征中去除其余n-k维特征。
2、新的k维具体代表的实际意义不知道，仅机器知道。
参考文档

二、 线性代数知识储备

1、 基变换的矩阵表示

一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。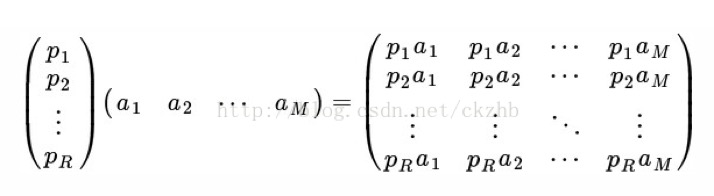
R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。

矩阵相乘找到了一种物理解释：
两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去（结果每一列表示一个维度m）。
更抽象的说，一个矩阵可以表示一种线性变换。

2、 协方差矩阵

-协方差（假设均值为0）：

$Cov\left( a,b\right) =\frac{1}{m} \sum^{m}_{i=1} a_{i}b_{i}$从直观上来看，协方差表示的是两个变量总体误差的期望。

-协方差矩阵：

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。

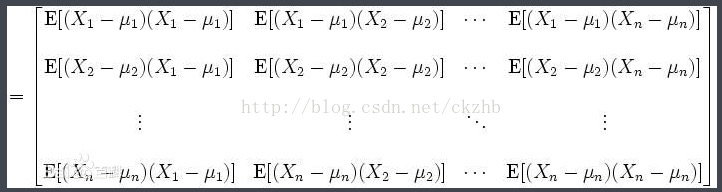
矩阵对角线位置上的值分别是元素的方差，而其他位置上的值是元素间的协方差。

• 在对角线上的元素越大，表明信号越强，变量的重要性越高；元素越小则表明可能是存在的噪音或是次要变量。
• 在非对角线上的元素大小则对应于相关观测变量对之间冗余程度的大小。

设A为原始数据矩阵，M为坐标变换矩阵，K为降维后数据矩阵，有：
$A_{N\times D}\cdot M_{P\times K}=L_{N\times K}$其中，A对应协方差矩阵C，L对应协方差矩阵D，D与C关系推导如下：
$C_{P\times P}=\frac{1}{N} A^{T}\cdot A$ $D=\frac{1}{N} \left( AM\right)^{T} \cdot \left( AM\right) =\frac{1}{N} \cdot M^{T}A^{T}AM$ $=M^{T}\left( \frac{1}{N} A^{T}A\right) M=M^{T}CM$目的：将D化为仅对角线处有值的对角矩阵

自此，求解坐标变换矩阵M的问题可转化为将实对称矩阵A做对角化求解由特征向量构成矩阵的问题。

特征值的大小表示对应特征向量的重要程度。
原数据矩阵A乘以将特征向量按大小从左到右排列则用前k列组成的矩阵M，就得到了我们需要降维后的数据矩阵L。

三、 PCA实现步骤

设有m条n维数据。

1. 将原始数据按列组成m行n列矩阵X。
2. 将X的每一列（代表一个属性字段）进行零均值化，即减去这一列的均值，做数据预处理。
3. 求出协方差矩阵Cov。
4. 求出协方差矩阵的特征值及对应的特征向量。
5. 将特征向量按对应特征值按大小从左到右排列成矩阵，取前k列组成矩阵P。
6. Y=XP即为降维到k维后的数据

四、程序实现

下面给出基于numpy库的Python实现

import numpy as np


def zeroMean(dataMat):
    average = np.mean(dataMat, axis=0)  # 按列求均值
    new_dataMat = dataMat - average
    return new_dataMat


def pca(dataMat, n):
    new_dataMat = zeroMean(dataMat)
    covMat = np.cov(new_dataMat, rowvar=0)  # covMat极为所求的协方差矩阵

    # Compute the eigenvalues and right eigenvectors of a square array.
    # 返回矩阵的特征值和特征向量
    # eigVects 每一列代表一个特征向量
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))

    eigValsSort = np.argsort(eigVals)  # argsort对特征值是从小到大排序,提取其对应索引号

    n_eigValsSort = eigValsSort[-1:-(n + 1):-1]  # 提取最大的n个特征值的下标
    n_eigVects = eigVects[:, n_eigValsSort]
    low_dataMat = new_dataMat * n_eigVects

    return low_dataMat