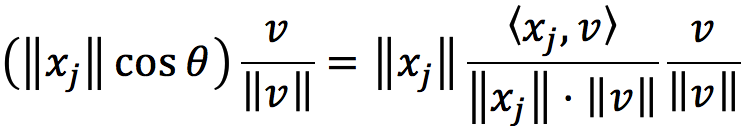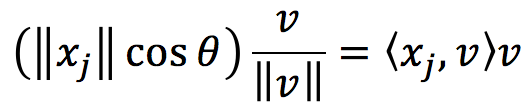基本思想
其基本思想就是设法提取数据的主成分(或者说是主要信息),然后摒弃冗余信息(或次要信息),从而达到压缩的目的。本文将从更深的层次上讨论PCA的原理,以及Kernel化的PCA。
引子
首先我们来考察一下,这里的信息冗余是如何体现的。如下图所示,我们有一组二维数据点,从图上不难发现这组数据的两个维度之间具有很高的相关性。因为这种相关性,我们就可以认为其实有一个维度是冗余的,因为当已知其中一个维度时,便可以据此大致推断出另外一个维度的情况。
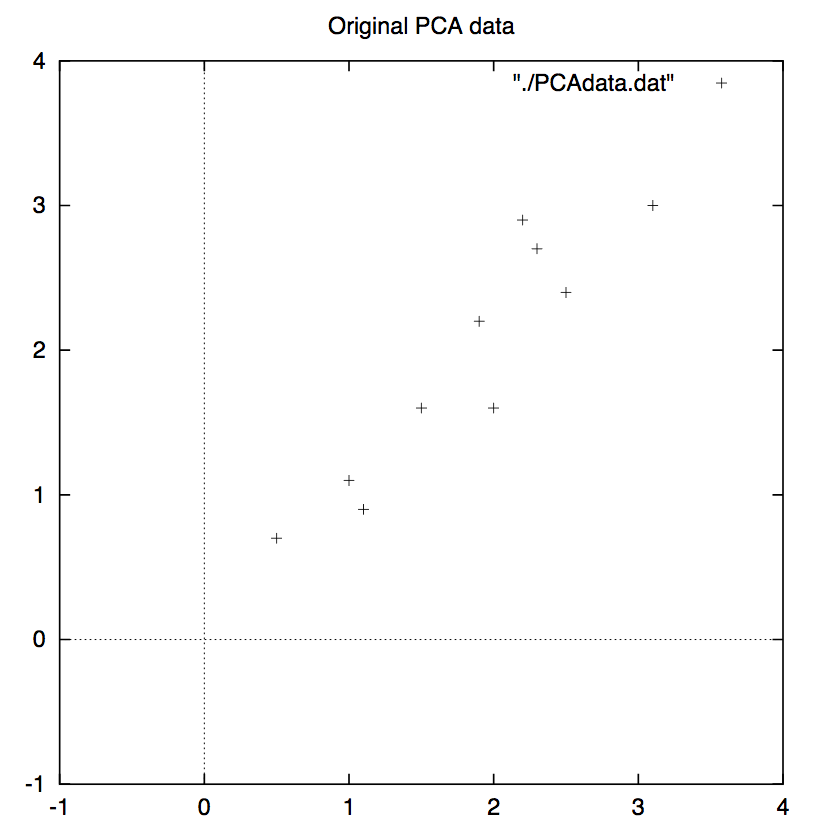
为了剔除信息冗余,我们设想把这些数据转换到另外一个坐标系下(或者说是把原坐标系进行旋转),例如像下图所示情况,当然这里通过平移设法把原数据的均值变成了零。

下图是经过坐标系旋转之后的数据点分布情况。你可以看出,原数据点的两个维度之间的相关性已经被大大削弱(就这个例子而言几乎已经被彻底抹消)。

同时你也会发现在新坐标系中,横轴这个维度x相比于纵轴那个维度y所表现出来的重要性更高,因为从横轴这个维度上更大程度地反应出了数据分布的特点。也就是说,本来需要用两个维度来描述的数据,现在也能够在很大程度地保留数据分布特点的情况下通过一个维度来表达。如果我们仅保留x这个维度,而舍弃y那个维度,其实就起到了数据压缩的效果。而且,舍弃y这个维度之后,我们再把数据集恢复到原坐标系上,你会发现关于数据分布情况的信息确实在很大程度上得以保留了(如下图所示)。
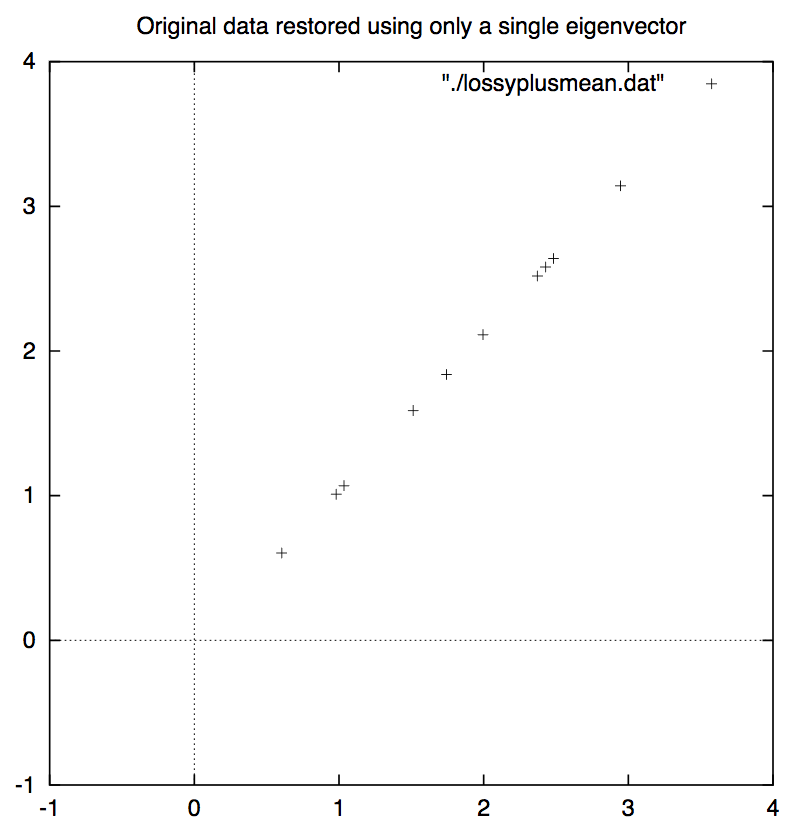
正式推导
上面所描述的也就是PCA要达到的目的。
但是,如何用数学的语言来描述这个目的呢?
或者说,我们要找到一个变换使得坐标系旋转的效果能够实现削弱相关性或将主要信息集中在少数几个维度上这一任务,应该如何确定所需之变换(或者坐标系旋转的角度)呢?
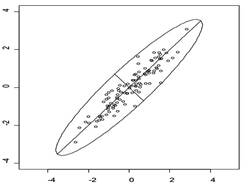
我们还是来看一个例子,假设现在有如下图所示的一些数据,它们形成了一个椭圆形状的点阵,那么这个椭圆有一个长轴和一个短轴。在短轴方向上,数据变化很少;相反,长轴的方向数据分散得更开,对数据点分布情况的解释力也就更强。
那么数学上如何定义数据“分散得更开”这一概念呢?没错,这里就需要用到方差这个概念。如下图所示,现在有5个点,假设有两个坐标轴w和v,它们的原点都位于O。然后,我们分别把这5个点向w和v做投影,投影后的点再计算相对于原点的方差,可知在v轴上的方差要大于w轴上的方差,所以如果把原坐标轴旋转到v轴的方向上,相比于旋转到w轴的方向上,数据点会分散得更开!

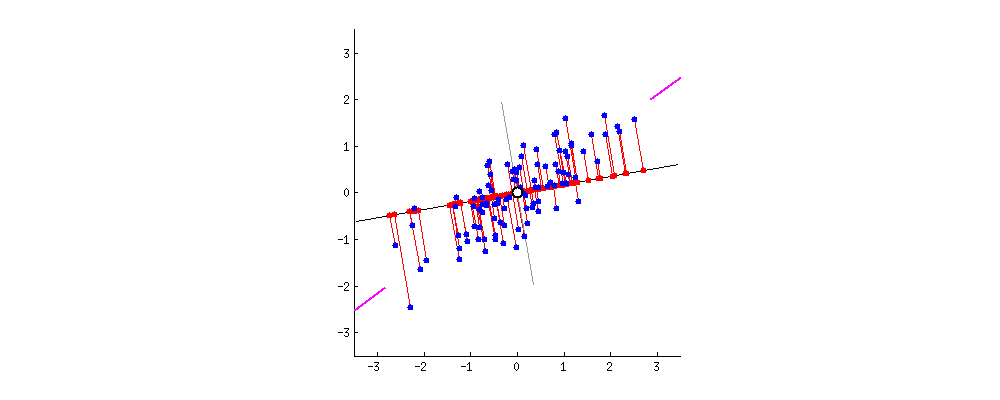
(动图链接:https://blog.csdn.net/baimafujinji/article/details/79376378)
假设训练样本的平均值为零。PCA的目标是在空间中找到一组包含最大方差量的向量。
上图中的一点 xj 向 v 轴做投影,所得之投影向量为
其中θ是向量Oxj与v的夹角。如果这里的向量v是单位向量,则有
这同时表明其系数其实就是内积
所有像素xj在该归一化方向v上的投影是
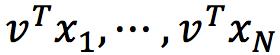
预测的方差是
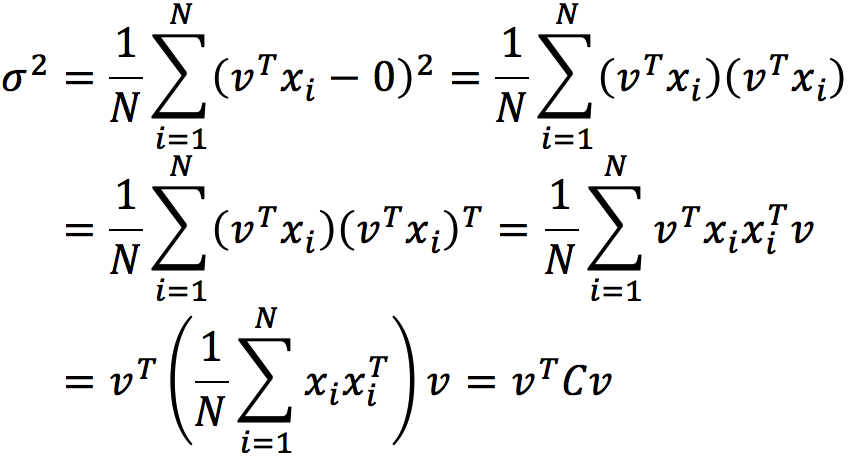
其中,C是协方差矩阵.
因为vTCv 就是 variance,而我们的目标是最大化variance,因此 the first principal vector can be found by the following equation:

鉴于是带等式约束的优化问题,遂采用拉格朗日乘数法,写出拉格朗日乘数式如下:
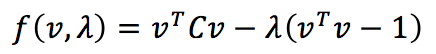
然后将上式对v和λ求导,并令导数等于0,则有

于是我们知道,原来的argmax式子就等价于find the largest eigenvalue of the following eigenvalue problem:
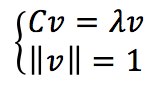
注意我们前面的argmax式子要算的是使得vTCv 达到最大的v,而v可以由上式解出,据此再来计算vTCv ,则有

也就是说我们要做的就是求解Cv=λv,从而得到一个最大的λ,而这个λ对应特征向量v所指示的就是使得variance最大的方向。Projections of the data on the principal axes are called 主成分, also known as PC scores。注意因为v是单位向量,所以点 xj 向 v 轴做投影所得之 PC score 就是 vT·xj。而且这也是最大的主成分方向。如果要再多加的一个方向的话,则继续求一个次大的λ,而这个λ对应特征向量v所指示的就是使得variance第二大的方向,并以此类推。
更进一步,因为C是Covariance matrix,所以它是对称的,对于一个对称矩阵而言,如果它有N个不同的特征值,那么这些特征值对应的特征向量就会彼此正交。如果把Cv=λv,中的向量写成矩阵的形式,也就是采用矩阵对角化(特征值分解)的形式,则有C=VΛVT,其中V是特征向量的矩阵(每列是特征向量),并且Λ是对角矩阵,其特征值λi在对角线上以递减的顺序。 特征向量称为主轴或数据的主方向。
注意到Covariance matrix(这里使用了前面给定的零均值假设)
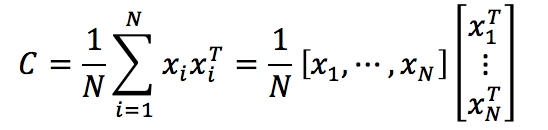
如果令,其中xi 表示一个列向量,则有
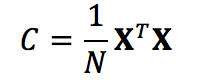
主轴上的数据投影称为主成分,也称为PC得分; 这些可以看作是新的,变换的变量。 第j个主要成分由XV的第j列给出。 新PC空间中第i个数据点的坐标由第i行XV给出。
---------------------
原文:https://blog.csdn.net/baimafujinji/article/details/79376378
---------------------
算法及实例
PCA算法
总结一下PCA的算法步骤:

实例
原始数据集矩阵X:

求均值后:

再求协方差矩阵:

特征值:
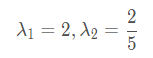
对应的特征向量:

标准化(其实不标准化也一样,只是稍显不专业)

选择较大特征值对应的特征向量:
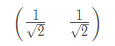
执行PCA变换:Y=PX,得到的Y就是PCA降维后的值数据集矩阵: