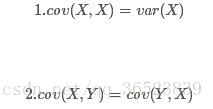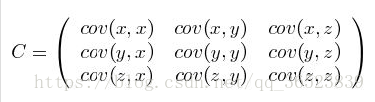本章关于PCA的代码虽少，但涉及到的知识却很多，由于数学知识比较浅薄，所以在看这章时提前查找资料复习了很多的概率论和统计学知识和python基础知识，这里记录的很多都是关于PCA的相关知识或理论（例如：特征向量、协方差矩阵等），由于部分知识涉及较多，讲的有点详细所以文章篇幅较长尽量缩减了，下面进入正文。

通常我们可以很清楚的看到一维数据，或直观的二维图形，但实际中很多的数据远不止1、2、3维，这些数据往往拥有超出显示能力的更多特征。数据显示并非大规模特征下的唯一难题，对数据进行简化还有如下一系列原因：

使得数据集更易使用；
降低很多算法的计算开销；
去除噪声点；
使得结果易懂。

降维技术：

主成分分析（Principal Component Analysis, PCA）。数据从原来的坐标系转化到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。重复选择新坐标轴，最终大部分方差都包含在最前面的几个新坐标轴中。。因此，忽略余下的坐标轴，达到降维的目的。

因子分析（Factor Analysis）。在因子分析中，我们假定在观察数据的生成中有一些观察不到的隐变量（latent variable）。假设观察数据时这些隐变量和某些噪声的线性组合。通过找到隐变量就可以实现数据的降维。

独立主成分分析（Independent Component Analysis, ICA）。ICA假设数据是从N个数据源生成的。假设数据位多个数据源的混合观察结果，这些数据源之间在统计上是相互独立的，而在PCA中假设数据是不相关的。同因子分析一样，如果数据源的数目少于观察数据的数目，则可以实现降维过程。

流行学习（manifold learning）。

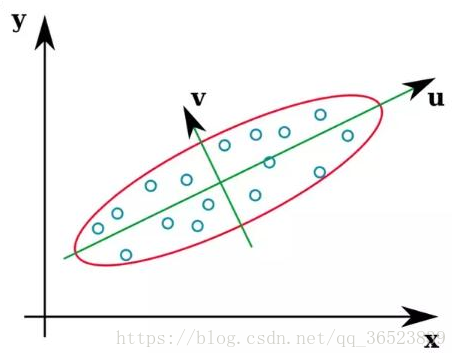
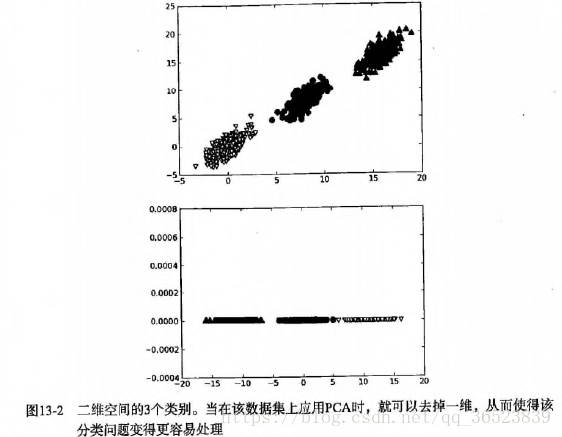
在这些流行的降维技术中，PCA是使用的最广泛的数据压缩算法，它的原理上面已经提到，就是移动坐标轴，而移动是由数据本身决定的（即每次都是寻找数据最大方差方向），降维后我们可以使用更简单的分类器或者得到更好的分类间隔，下图说明：

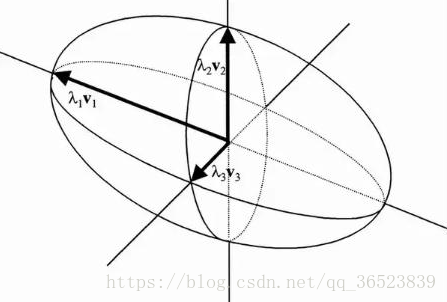
这些样本的协方差矩阵的特征向量是u、v，在第一次移动坐标轴时，先找到了数据的最大方差方向，即此时的u方向，接着第二次移动坐标轴，找到的次大方差方向且与u轴正交的v方向。可以看到第一个特征向量（从数据的平均值）指向欧几里德空间中数据方差最大的方向，第二个特征向量跟第一特征向量是垂直的。在三维空间中，也就是第三特征向量存在时如下：

此时的三个特征向量相互正交，构成了三维空间下的坐标（v1、v2、v3）。

讨论了通过坐标轴旋转的方法，但是这并没有解决降维的问题，如何通过坐标轴的旋转来降维呢？

前面提到的第一个主成分就是从数据差异性最大的（即方差最大）的方向提取出来的，第二个主成分则来自于数据差异性次大的方向，并且与第一个主成分方向正交。通过数据集的协方差矩阵及其特征值分析，我们就可以求得这些主成分的值。

一旦得到了协方差矩阵的特征向量，我们就可以保留最大的N个值。这些特征向量也给出了N个最重要特征的真实结构。我么可以通过将数据乘上这N个特征向量而将它转换到新的空间，以此达到了降维的目的。

补充相关知识：

好了上面已经把PCA降维的原理说了一遍，下面补充相关知识更仔细的解释请参考这里（如果知道了可以跳过）：

方差：

最先提到的一个概念，也是旋转坐标轴的依据。之所以使用方差作为旋转条件是因为：最大方差给出了数据的最重要的信息。

协方差：

用来衡量两个变量的总体误差，方差是协方差的一种特殊情况，即当两个变量相同。可以通俗的理解为：两个变量在变化过程中是否同向变化？还是反方向变化？同向或反向程度如何？取值为负∞到正∞仿照方差的定义，度量各个维度偏离其均值的程度，定义为：

由协方差的定义可以推出两个性质：

协方差矩阵：

协方差只能处理二维问题（即两个特征X、Y），维数多了自然需要计算多个协方差，比如n维的数据集需要计算 $\frac{n!}{(n-2)!*2}$ 个协方差，自然而然我们会想到使用矩阵来组织这些数据，协方差定义：

可见，协方差是一个对称的矩阵，且对角线是各维度上的方差。正是由于协方差矩阵为对称矩阵所以矩阵分解后特征值所对应的特征向量一定无线性关系，且相互之间一定正交，即内积为零。

特征向量：

对协方差矩阵的特征向量最直观的解释之一是它总是指向数据方差最大的方向（上面的u、v）。所以我们需要求得协方差矩阵，然后计算出其特征向量，通过对特征值的排序，选出我们要求的N个特征向量（即N个最重要特征的真实结构），用原数据乘上这N个特征向量而将它转换到新的空间中。（在numpy中linalg的eig方法可以求得特征值、特征向量，对特征值排序后选择最大的特征向量）

将二维特征降转为一维效果如下图（其它维数脑补）：

python代码实现PCA降维处理：

伪代码：

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的N个特征向量
将数据转换到上述N个特征向量构建的新空间中

代码：

样例数据：

from numpy import *
import matplotlib.pyplot as plt

# 加载本地数据
def loadDataSet(fileName,delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [list(map(float,line)) for line in stringArr]  # py3需要注意使用list改变数据类型
    return mat(datArr)  # 转换为二维的数组便于运算

# pca降维函数  （原始数据 压缩维数）  不指定压缩维数默认9999999即维数全部返回
def pca(dataMat,topNfeat=9999999):
    meanVals = mean(dataMat,axis=0)  # 按列求均值
    meanRemoved = dataMat - meanVals             # 去平均值每个值减去该列的平均值（后面有解释为什么要去均值）
    #计算协方差矩阵，除数n-1是为了得到协方差的无偏估计
    #cov(X,0) = cov(X) 除数是n-1(n为样本个数)
    #cov(X,1) 除数是n
    covMat = cov(meanRemoved,rowvar=0)           # 协方差矩阵计算 （rowvar=0 后面有解释这个参数的重要意义）
    eigVals,eigVects = linalg.eig(mat(covMat))   # 分解计算协方差矩阵的（特征值 特征向量）
    eigValInd = argsort(eigVals)                 # 获取从小到大排序特征值的下标 于sort有差别
    eigValInd = eigValInd[:-(topNfeat+1):-1]     # 获得最大的特征值的下标N个 (起始位置:结束位置:步长   步长为负则从右往左取；结束位置步长同时为负则从右排列向左排列)
    redEigVects = eigVects[:,eigValInd]          # 保留N个特征值最大列的特征向量 (即数据方差最大的N个方向)
    lowDDataMat = meanRemoved * redEigVects      # 将数据转换到新空间 （用特征向量*数据集）
    reconMat = (lowDDataMat * redEigVects.T) + meanVals # 利用降维后的矩阵反构出原始矩阵（作用：用作测试，可以和未压缩的原矩阵比较）
    return lowDDataMat,reconMat   # 压缩后的矩阵 反构出的原始矩阵

dataMat = loadDataSet('testSet.txt')
lowDMat,reconMat = pca(dataMat,1)    # 返回了 降维后的数据 反构出的原始数据

# 画图
fig = plt.figure()
ax = fig.add_subplot(111)
# ax.scatter(lowDMat[:,0].flatten().A[0],zeros(len(lowDMat)))   # 降维后的图
ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)
ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=50,c='red')
plt.show()

解释：减去均值后再除以标准差得出的数值就是标准化数据，例如：影响某国居民体重的两个因素是收入和运动量，这两个因素的均值分别是50000元和50小时，标准差是2000元和1小时，那么你就很难比较这两因素的变动对体重的影响，所以就要标准差，减去均值再除以标准差得出的数据就表示“偏离均值多少个标准差”，就能够在回归时比较各自对体重的影响程度！

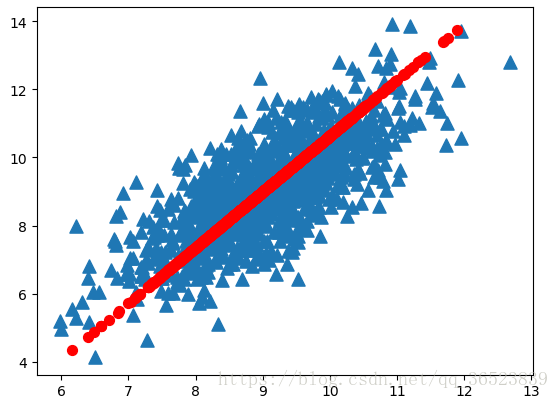
三角形：原始数据圆形：第一主成分

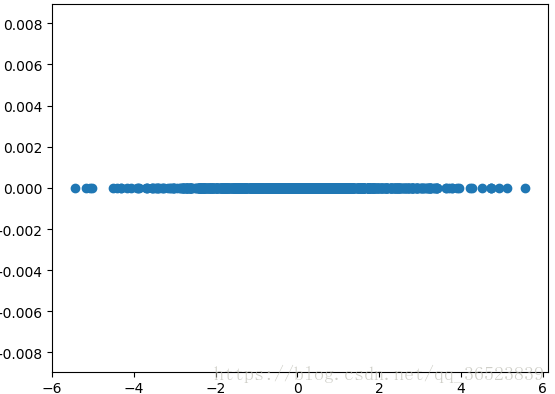
降维数据如下图：

示例：利用PCA对半导体制造数据降维（590维特征）

（调用函数之前需要构造一个函数来处理数据中的空值NaN，这里使用均值代替。我试过pandas数据来处理很方便也很好理解，但是运行速度慢了太多。）

# 示例 半导体数据降维

# 将NaN值置换为平均值
def replaceNanWithMean():
    datMat = loadDataSet('secom.data',' ')  # 解析数据
    numFeat = shape(datMat)[1]      # 获取特征维度
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) # 利用该维度所有非NaN特征求取均值
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal # 将该维度中所有NaN特征全部用均值替换
    return datMat

dataMat = replaceNanWithMean()
meanVals = mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals
covMat = cov(meanRemoved, rowvar=0)
eigVals, eigVects = linalg.eig(mat(covMat))
print(sum(eigVals)*0.9)     # 计算90%的主成分方差总和
print(sum(eigVals[:6]))     # 计算前6个主成分所占的方差
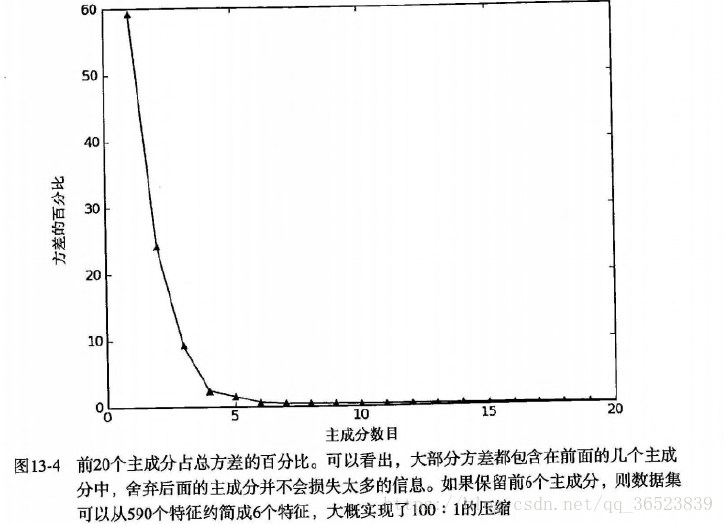
plt.plot(eigVals[:20])      # 对前20个画图观察
plt.show()

特征值中超过20%的值都为0：

sklearn的PCA处理：

同时我们使用sklearn中PCA处理方法来做步骤更为简单的处理，并与上面的结果作比较：

from sklearn.decomposition import PCA
pca = PCA()      # n_components参数选择降维程度
pca = pca.fit(replaceNanWithMean()) # fit_transform()为转换数据
main_var = pca.explained_variance_  # 特征值
print(sum(main_var)*0.9)        #下面与手写代码作比较
print(sum(main_var[:6]))
plt.plot(main_var[:20])
plt.show()

将两种方法作比较：

效果不错，与上面作者提供的代码相差无几,前6个主成分覆盖了96.8%的方差，前20个主成分覆盖了99.3%的方差。如果保留前6个而去除后584个主成分，就可以实现大概100：1的压缩比。有效的主成分数目取决于数据集和具体应用。上面显示我们编写的程序得到主成分的90%为81131452.77696137与sklearn计算得出的81131452.7769614几乎一致。前6个也几乎一样。

以上为全部内容，部分知识为个人理解，如有问题，请指出，在学习过程中参考了一些资料，十分感谢，如果由需要可以前去查看。

主要参考书籍：《机器学习实战》

参考文章：http://www.360doc.com/content/17/0810/21/37752273_678258912.shtml 特征变量解释

参考文章：https://www.cnblogs.com/zy230530/p/7074215.html 部分代码解释

参考文章：https://zhidao.baidu.com/question/1800959389164413707.html 减去标准差解释

参考文章：https://blog.csdn.net/u010454729/article/details/48811029 sklearn部分解释

参考文章：https://blog.csdn.net/qq_36523839/article/details/82259634 协方差矩阵解释

机器学习实战——PCA（主成分分析）

方差：