Perlin Noise是一种Gradient Noise,是基于网格梯度的噪声。你可能会疑惑,为什么它能得到效果很好的噪声效果,现在来探究一下它的本质。
大多数时候我们接触到的是二维的Perlin Noise,也就是下面这种情况:在二维网格中每个节点生成一个梯度向量,然后每个点跟周围的梯度点乘,最后使用平滑函数做插值。

这个流程比较复杂,我们先从相对简单的一维Perlin Noise开始:
一维Perlin Noise
一维Perlin Noise的定义是类似的,在一个一维坐标系中,每个网格点有一个梯度向量(此时为一个值),由于梯度要归一化,所以只有两个值-1或者1。
我们先不考虑两个节点梯度的混合,只考虑一个梯度对附近点的影响。如下图假设0点处的梯度为G0,我们考虑当x在-1和1之间时,G0对最终Noise值的贡献。很容易知道结果为G0*x,因为不管是左侧还是右侧,距离向量都是x(左侧是0-(-x)),也就是说这是一个线性函数,斜率为正负1。

然后我们考虑梯度的混合:

如上图,假设自变量范围是(x1,x2),在本例中x1=0,x2=1。设x1处梯度G=a,x2处梯度=b。t是将(x1,x2)归一化的变量(本例中t=x),根据0点到t点的向量为t,1点到t点的向量为1-t,可以得到插值后的结果P:
这里f代表使用的平滑函数,在t=x且使用线性平滑的情况下有f=t=x,此时P(x)是x的一个二次函数,并且可以化简为:
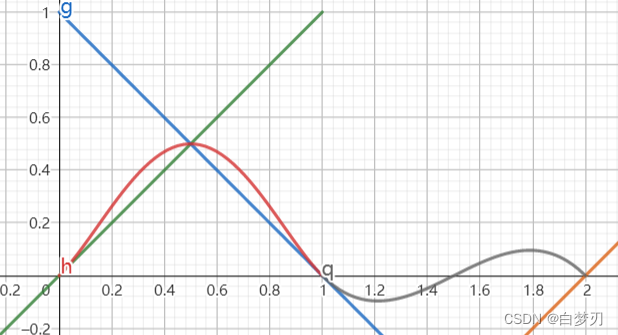
根据上式,不妨设a = 1, b = -1,我们来看看插值后的结果是什么样的

详情点击Calculator Suite - GeoGebra,红色的二次函数就是插值的结果,这里同时列出了0和1两点处的梯度的线性贡献,分别表示为绿色和蓝色线条,二次函数实际上就是对这两个线性函数使用了一次线性混合。
为什么我们一般不用线性平滑呢?这是因为使用线性平滑没法保证边界处导数平滑。为了看到这一点,我们将上述的推导平移到1~2范围内,并假设2点处的梯度为c,经过一番推导可以得到1~2范围内的结果:
假设c=-1,图像如图(注意右下角的灰色线):

这时在t=1处还是平滑的,但是当c=1时就不平滑了,这是因为此时b+c=0,导致f(x)恒为0。

那么在x=1处就会产生不平滑的感觉。消除的办法就是使用高阶平滑函数,关于平滑可以参考我之前的文章像素平滑公式比较_白梦刃的博客-CSDN博客,这里分别给出了使用三阶和五阶多项式平滑的结果:

可以看到,它做的是让t=1处有一个渐变的过渡,同时在右边做了平衡。
实际上,根据之前的P(t)式子可以直接求出P(t)的导数,P(x)的导数和P(t)的导数只差一个常数乘积:
由于平滑函数都假定边界点处的导数为0,即f'(0)=f'(1)=0,容易验证P'(0)=a,P'(1)=b,说明梯度实际上就是给定点的导数。
我们可以总结一下思路,梯度给出网格节点处的导数,生成的结果是对节点处切线函数的混合。
这一点同样可以推广到二维场景,只是表述上有区别。
二维Perline Noise
首先仍然先考虑一个梯度对附近点的影响,假设0点处的梯度G(a,b),参考下图,很显然不论p在哪个区间,原点处梯度的贡献为x*a+y*b。

x*a+y*b实际上是一个空间中的平面函数,这个函数在x轴和y轴上的偏导数分别是a和b,也就是说这个函数以G(a,b)作为它的偏导数,在N维度(N>2)的情况,这其实就是梯度向量,也是Gradient Noise名称的由来。
由于参数太多,不好写出整体的混合式,所以这里直接给出混合后的结果:

曲面就是最终得到的噪声值,在四个角处各有小平面代表那一点的梯度的贡献,可见其与噪声曲面相切。详情参考Calculator Suite - GeoGebra
总结一下思路,梯度给出网格节点处噪声曲面的偏导数(梯度),生成的结果是对节点处切平面的混合。
最后给出结论:
Perline Noise是这样工作的,首先设置好各个网格节点处的导数/梯度,最终生成一个曲线/曲面,其在节点处的导数/梯度和设置的值相同,其他值由各个节点处切线/切平面根据权重插值得到。
局限性
函数值局限性
Perline Noise实际上也有局限性,有一个经常不为人所知的特性就是,Perline Noise实际上在网格点处的值恒为0。
以二维的举例,如下图当p在第一象限接近原点时,按照双线性差值实际上只需要考虑原点处的值,距离向量p(x,y)接近(0,0),这样它与原点梯度G(a,b)的点乘结果自然也接近于0。同理可以推出所有网格点都是一样。

这代表用Perlin Noise生成的噪声,实际上在网格点处都位于中间位置(-1<0<1),这些网格点约束了最终生成的形状,这意味着它生成的图形保持一种均衡性,不会偏移平衡位置太远。
很多时候这是我们想要的,你可以用它生成一个很好的平缓地形平面。但它也带来了限制,比如无法使一个网格内所有点值大于0或者小于0,也无法生成占据很大块区域的高山和峡谷。
解决这个问题需要使用一个基础平面,它具有较大的值域范围,使用它作为基础偏移而Perlin Noise作为细节调整部分。这个基础平面的生成可以使用低频的Value Noise或者Perlin Noise。
二阶导数局限性
Perline Noise除了固定了网格点处的值为0,还固定了二阶导数。参考一维的这个公式,求出其二阶导数:
如果使用三阶平滑公式,则P''(0)=-6b,P''(1)=-6a,这导致网格点左右导数不平滑。 如果使用五阶平滑公式,则P''(0)=P''(1)=0,导数平滑,但固定了网格点处的二阶导数恒为0。
理论上如果我们知道网格点处的二阶导数,那么可以用跟之前Value Noise类似的方法来做更高级的平滑。像素平滑公式比较_白梦刃的博客-CSDN博客
但实际上我们没有办法求出二阶导数,之前的方法是用数值微分方法求的导数。但是Perlin Noise没有办法使用因为它在网格点处的值恒为0。
但在有一种情况下可以使用,就是我们在Perlin Noise底部增加一个基础Offset,比如说由Value Noise生成,这样每个网格点上有不同的基础值,可以通过数值微分计算出二阶导数,效果会比直接相加要好。