这篇文章,同一个人(团队?)写的,遗憾的是,没怎么看懂。怎么说呢,里面的关于对偶的性质实在不知道从何入手,但想来还是得记一笔。
引
这篇文章,讨论的是这样的一个问题,有一个矩阵\(M \in \mathbb{R}^{n_1 \times n_2}\),但是因为种种原因,我们只能知晓其中的一部分元素即\(P_{\Omega}(M)\),那么问题来了,有没有办法能够恢复\(M\)呢,或者说在什么条件下我们能恢复\(M\)呢(实际上,这个问题好像是作者前一篇论文已经给出了答案)?然后,又有新的困难,因为我们的观测是有误差的,也就是说我们观测到的实际上不是\(P_{\Omega}(M)\),而是\(P_{\Omega}(M+Z)\)。
作者总拿Netflix举例子,类似地,我们可以用网易云来举例子(虽然估计网易云的推荐方法和这个并没有啥大关系)。
我们可以这么想,\(M\)的每一行是一个用户,每一列是一首歌,其中的每一个元素是该用户给这首歌打的分(当然,这个分可能是通过一些操作的判断的,比如收藏,评论,下载,是否跳过等等)。显然,一个用户不可能听过里面的所有的歌,一首歌也没法让所有人都听(打分),所以,我们所见识到的是\(P_{\Omega}(M)\),一个稀疏的矩阵。然而,推荐歌曲,关注的就是那些用户没有听过的但可能被打高分的歌,所以我们要做的就是利用\(P_{\Omega}(M)\)恢复出\(M\)。听起来的确蛮好玩的。
然后问题是,恢复需要什么前提。很显然,如果一首歌没有被人听过,或者该用户没有听过任何歌,肯定没法把分数恢复出来,因为这跟瞎猜没分别,所以,假设就是\(M\)低秩,但是每行每列不能全为零。
和之前一样,作者采用不连贯条件来描述:

恢复1
本来,是应该求解下述问题的:
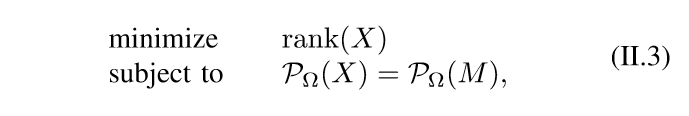
但是,这个问题很难求解(NP-hard)。
然后\(\mathrm{rank}\)的凸放松是\(\|\cdot\|_*\)核范数,所以:
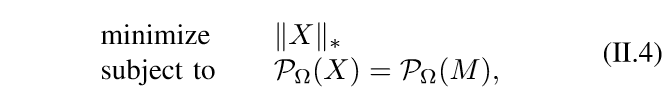
核范数与SDP
然后,作者指出,核范数可以通过对偶,转换成一个半正定规范问题(看这篇论文最大的收获吧)。
\[ \|X\|_* \le y \Leftrightarrow 存在对称矩阵W_1,W_2 使得 M:= \left [ \begin{array}{cc} W_1 & X \\ X^T & W_2 \end{array} \right ] \succeq 0, \mathrm{Tr} W_1 + \mathrm{Tr} W_2 \le 2y \]
先来前推后,只要构造出这么一个\(W_1\)就可以了。假设\(X = U\Sigma V^T, \Sigma \in \mathbb{R}^{r \times r}\),\(W_1 = U\Sigma U^T,W_2=V\Sigma V^T\)。那么,\(\mathrm{Tr} W_1 + \mathrm{Tr} W_2 \le 2y\)容易证明,第一个条件这么来玩:
\[ [z_1^T, z_2^T] \left [ \begin{array}{cc} W_1 & X \\ X^T & W_2 \end{array} \right ] \left [ \begin{array}{c} z_1\\ z_2 \end{array} \right ] \]
再令\(a = U^Tz_1, b = V^Tz_2\),可得:
\[ [z_1^T, z_2^T] \left [ \begin{array}{cc} W_1 & X \\ X^T & W_2 \end{array} \right ] \left [ \begin{array}{c} z_1\\ z_2 \end{array} \right ] = (a+b)^T \Sigma (a+b) \ge 0 \]
对于任意的\(z_1, z_2\)成立,所以半正定条件也得证了。
好了,现在来反推:
\(\|X\|_* = \sup \{\mathrm{Tr}(X^TW)|\|W\|\le 1\}\),其中\(\|\cdot\|\)表示谱范数。
注意\(\|A\|_* \le \mathrm{Tr}(A)\),当\(A\)为半正定矩阵的时候。
所以
\[ \|M\|_* \le \mathrm{Tr}(M)=\mathrm{Tr}(W_1+W_2)\le 2y \]
又\(\|M\|_* = \sup \{\mathrm{Tr}(M^TW)|\|W\|\le 1\}\),所以
\[ \mathrm{Tr}(M^TW) \le 2y \]
又
\[ N := \left [ \begin{array}{cc} U^T & 0 \\ 0 & V^T \end{array} \right ] M \left [ \begin{array}{cc} 0 & I_{n_1 \times n_1} \\ I_{n_2 \times n_2} & 0 \end{array} \right ] \left [ \begin{array}{cc} V & 0\\ 0 & U \end{array} \right ] = \left [ \begin{array}{cc} \Sigma & U^TW_1U \\ V^TW_2V & \Sigma \end{array} \right ] \]
令
\[ W = \left [ \begin{array}{cc} 0 & I_{n_1 \times n_1} \\ I_{n_2 \times n_2} & 0 \end{array} \right ] \left [ \begin{array}{cc} V & 0\\ 0 & U \end{array} \right ] \left [ \begin{array}{cc} U^T & 0 \\ 0 & V^T \end{array} \right ] = \left [ \begin{array}{cc} 0 & UV^T \\ VU^T & 0 \end{array} \right ] \]
容易证明\(\|W\| \le 1\),所以\(\mathrm{Tr}(N) = \mathrm{Tr}(M^TW)=2\|X\|_*\le 2y\),故\(\|X\|_* \le y\)得证。但愿没出错。。。
然后,论文就给出了第一个定理,关于恢复的:

这个结果貌似是之前的工作,,满足一定条件,\(M\)就会有很大概率被恢复。
然后呢,论文又提了以下加强版的不连贯条件:

然后有相应的定理2:

然后跳过。
稳定恢复
用户的评分是不一定正确,不同的场合,不同的天气可能就会给出不同的分数,如果是机器推断的分数那就更是如此了。所以,我们观测的部分数据实际上不一定是\(P_\Omega (M)\),而是\(P_\Omega (Y) = P_\Omega (M+Z)\),其中\(Z\)是类似噪声的存在。
假设,\(\|P_{\Omega}(Z)\|_F \le \delta\),求解下列问题:
\[ \begin{array}{cc} \min & \|X\|_* \\ s.t. & \|P_{\Omega}(X-Y)\|_F \le \delta \end{array} \]
这个问题同样可以作为SDP求解,假设其解为\(\hat{M}\)。有如下定理:

但是问题是,我们从何知道\(\delta\)呢?而在实际操作的时候,作者是求解下述问题:
\[ \min \quad \frac{1}{2} \|P_{\Omega} (X-Y)\|_F^2 + \mu \|X\|_* \]
作者说,这个问题是上面那个问题的对偶结果,饶了我吧,有点像,但是整不出来。然后,不同的情况,作者也给出了\(\mu\)的一些选择。
作者还拿上面的结果和下面的神谕问题进行了比较:
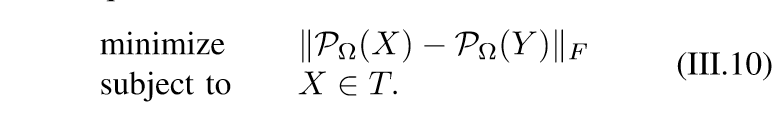
这个神谕,就是指,我们已经知道\(X \in T\)里面了,然后用了对偶还是共轭算子?晕了已经。就这样吧,再看我就得吐了。