信号与系统2022春季作业-第14次作业

 

  ◎ 本文网络下载链接： 信号与系统2022春季作业-第14次作业 : https://zhuoqing.blog.csdn.net/article/details/125103375

§01 基础作业

---

1.1 离散傅里叶变换

1.1.1 数据采样参数

  利用 FFT 处理器来计算采集数据的频谱。 要求频谱分析指标：
  （1） 频率间的分辨率 $f_1\le 10Hz$ ；
  （2） 信号频谱中最高频率 $f_{MAX}\ge 5kHz$ ；
  （3） 为了适应 FFT 算法， 采样数据点数 $N$ 需要为 2 的整数次幂；

  根据上述数据频谱分析指标要求， 试确定：
  （1） 数据采样时间间隔 $T_s$ ；
  （2） 采样数据点数 $N$ ；

1.1.2 频谱分析计算量

  已知序列 $x\left[n\right]$ 数据程度为 240； $h\left[n\right]$ 数据长度为 14。
  （1） 直接使用（线）卷积计算 $x\left[n\right]\ast h\left[n\right]$ ， 给出实数乘法次数和实数加法次数；
  （2） 利用 基-2 快速傅里叶变换（即基于 2 分法设计快速傅里叶变换）完成 $x\left[n\right],h\left[n\right]$ 之间的线卷积， 所需要的实数乘法次数和加法次数；
  （3） 比较以上结果， 并得到你的结论。

1.1.3 数据频谱分析时间

• 本题为思考题

  序列 $x\left[n\right]$ 的长度为 4906。 已知一款单片机每次完成单精度实数乘法和加法所需要的时间为 $20\mu s$ 和 $2.5\mu s$ 。请分析直接计算 D F T { x [ n ] } DFT\left\{ {x\left[ n \right]} \right\} DFT{ x[n]} 和 F F T { x [ n ] } FFT\left\{ {x\left[ n \right]} \right\} FFT{ x[n]} 个需要多少时间？

1.1.4 对比线卷积与圆卷积

  已知 $x\left[n\right],h\left[n\right]$ 的长度分别为 10,25。 它们的（线）卷积为 $$y_1\left[n\right]=x\left[n\right]\ast h\left[n\right]$$

  下面利用 DFT 求它们之间长度为 25 的 圆卷积 $y_2\left[n\right]$ 。先计算两个序列的DFT： X [ k ] = D F T { x [ n ] } X\left[ k \right] = DFT\left\{ {x\left[ n \right]} \right\} X[k]=DFT{ x[n]} ， H [ k ] = D F T { h [ n ] } H\left[ k \right] = DFT\left\{ {h\left[ n \right]} \right\} H[k]=DFT{ h[n]} ；再将两个序列的 DFT 相乘， $Y\left[k\right]=X\left[k\right]\cdot H\left[k\right]$ ；最后通过 DFT 反变换 y 2 [ n ] = D F T − 1 { Y [ k ] } y_2 \left[ n \right] = DFT^{ - 1} \left\{ {Y\left[ k \right]} \right\} y2​[n]=DFT−1{ Y[k]} 。

  试分析一下， 在 $y_1\left[n\right],y_2\left[n\right]$ 两个序列中， 相同取值的数据由多少个？

1.1.5 求两个序列反变换

• 本题问思考题

  已知 $x\left[n\right],y\left[n\right]$ 为 $N$ 点的实数序列， 它们的离散傅里叶变换为 X [ k ] = D F T { x [ n ] } ,    Y [ k ] = D F T { y [ n ] } X\left[ k \right] = DFT\left\{ {x\left[ n \right]} \right\},\,\,Y\left[ k \right] = DFT\left\{ {y\left[ n \right]} \right\} X[k]=DFT{ x[n]},Y[k]=DFT{ y[n]} 设计一个从 $X\left[k\right],Y\left[k\right]$ 求 $x\left[n\right],y\left[n\right]$ 的 $N$ 点的离散傅里叶反变换的算法， 为了提高运算效率，要求改运算能够一次完成。

提示： 下面给出利用DFT同时完成两个实数序列的DFT计算过程。 仿照这个过程，大家设计同时求两个实数序列反变换过程。
$x_1\left[k\right],x_2\left[k\right]$ 是实序列，将其构成复序列 $y\left[k\right]=x_1\left[k\right]+j\cdot x_2\left[k\right]$ D F T { x 1 [ k ] + j ⋅ x 2 [ k ] } = Y R [ m ] + j ⋅ Y I [ m ] DFT\left\{ {x_1 \left[ k \right] + j \cdot x_2 \left[ k \right]} \right\} = Y_R \left[ m \right] + j \cdot Y_I \left[ m \right] DFT{ x1​[k]+j⋅x2​[k]}=YR​[m]+j⋅YI​[m] D F T { x 1 [ k ] − j ⋅ x 2 [ k ] } = Y R [ ( − m ) N ] − j ⋅ Y I [ ( − m ) N ] DFT\left\{ {x_1 \left[ k \right] - j \cdot x_2 \left[ k \right]} \right\} = Y_R \left[ {\left( { - m} \right)_N } \right] - j \cdot Y_I \left[ {\left( { - m} \right)_N } \right] DFT{ x1​[k]−j⋅x2​[k]}=YR​[(−m)N​]−j⋅YI​[(−m)N​] 那么 D F T { x 1 [ k ] } = 1 2 { Y R [ m ] + Y R [ ( − m ) N ] + j ⋅ ( Y I [ m ] − Y I [ ( − m ) N ] ) } DFT\left\{ {x_1 \left[ k \right]} \right\} = {1 \over 2}\left\{ {Y_R \left[ m \right] + Y_R \left[ {\left( { - m} \right)_N } \right] + j \cdot \left( {Y_I \left[ m \right] - Y_I \left[ {\left( { - m} \right)_N } \right]} \right)} \right\} DFT{ x1​[k]}=21​{ YR​[m]+YR​[(−m)N​]+j⋅(YI​[m]−YI​[(−m)N​])} D F T { x 2 [ k ] } = 1 2 j { Y R [ m ] − Y R [ ( − m ) N ] + j ⋅ ( Y I [ m ] + Y i [ ( − m ) N ] ) } DFT\left\{ {x_2 \left[ k \right]} \right\} = {1 \over {2j}}\left\{ {Y_R \left[ m \right] - Y_R \left[ {\left( { - m} \right)_N } \right] + j \cdot \left( {Y_I \left[ m \right] + Y_i \left[ {\left( { - m} \right)_N } \right]} \right)} \right\} DFT{ x2​[k]}=2j1​{ YR​[m]−YR​[(−m)N​]+j⋅(YI​[m]+Yi​[(−m)N​])}

1.2 滤波器设计

1.2.1 物理可实现性

  设滤波器的频率特性对应的幅度平方函数表达式为：

  （1） $${\left|H\left(j\Omega \right)\right|}^2=\frac{1}{{\Omega }^4+{\Omega }^2+1}$$
  （2） $${\left|H\left(j\Omega \right)\right|}^2=\frac{100-{\Omega }^4}{{\Omega }^4+20{\Omega }^2+10}$$

  请问，上述系统中是否是物理可实现？

提示： 请参考佩里（Paley）-维纳（Wiener）准则中的两个条件。

1.2.2 滤波器结构图

  根据一下数字滤波器的系统函数，绘制出滤波器的结构图。

$$\left(1\right)H_1\left(z\right)=\frac{1}{1-a{z}^{-1}};\left(2\right)H_2\left(z\right)={\left(1-z^{-1}\right)}^3;$$$$\left(3\right)H_3\left(z\right)=\frac{1-z^{-1}}{1-a{z}^{-1}};\left(4\right)H_4\left(z\right)=\frac{{\left(1-z^{-1}\right)}^2}{1-\left(a_1+a_2\right)z^{-1}+a_3{z}^{-2}}$$$$\left(5\right)H_5\left(z\right)=\frac{0.28z^2+0.192z+0.05}{z^3+0.65z^2+0.55z+0.03}$$

• 思考题
    对于上面 $H_5\left(z\right)$ 对应的 IIR 数字滤波器，给出它的 直接 II 型， 级联型，并联型的滤波器结构图。

提示： 可以使用 MATLAB 辅助进行因式分解。

1.2.3 滤波器转换

  已知模拟滤波器的传递函数为：
  （1） $$H\left(s\right)=\frac{5}{\left(s+2\right)\left(s+3\right)}$$
  （2） $$H\left(s\right)=\frac{3s+2}{2s^2+3s+1}$$

  设采样周期 $T=0.5s$ ，用以下方法将其转换为数字滤波器：
  （1） 脉冲响应不变法；
  （2） 双线性变换法；

§02 实验作业

---

2.1 设计FIR滤波器

  使用窗函数法设计一个线性相位 FIR 低通滤波器， 要求的技术指标为：
  （1） 通带内在 ${\Omega }_p=30\pi rad/s$ 处衰减 ${\delta }_p\ge -3dB$ ；
  （2） 阻带内在 ${\Omega }_s=46\pi rad/s$ 处商检 ${\delta }_s\le -40dB$ ；
  （3） 采样周期 $T=0.01s$ 。

2.2 匹配滤波器

2.2.1 声音信标

  在全国大学生智能车竞赛竞赛中， 声音信标发送出频率线性变化的 Chirp 声音信号， 接受信号通过对比调频无线接收机得到的声音信号与麦克风测量的声音信号，获得信标相对于麦克风的声音延迟，进而可以获得信标的方位。

  下图是在 室外声音信标可行性分析中给出的发送Chirp信号与麦克风接收到的信号。

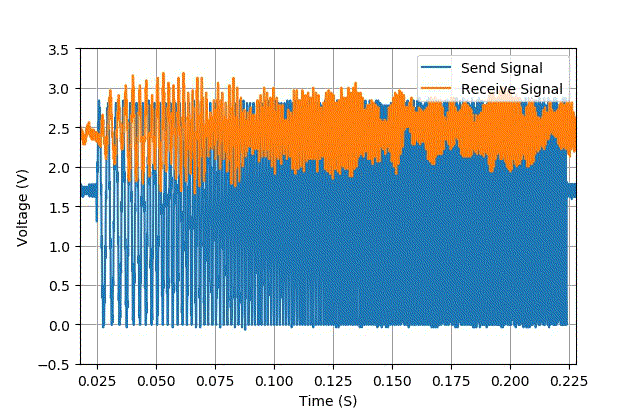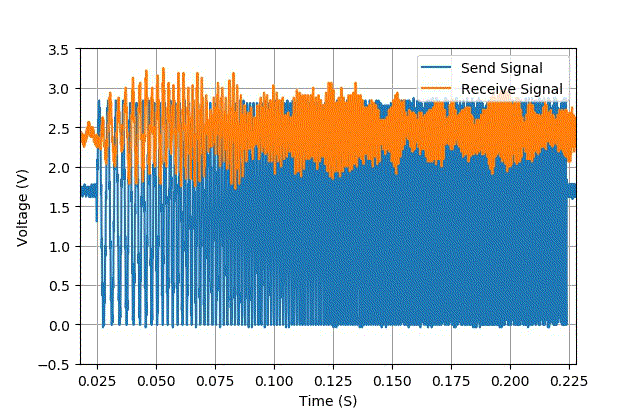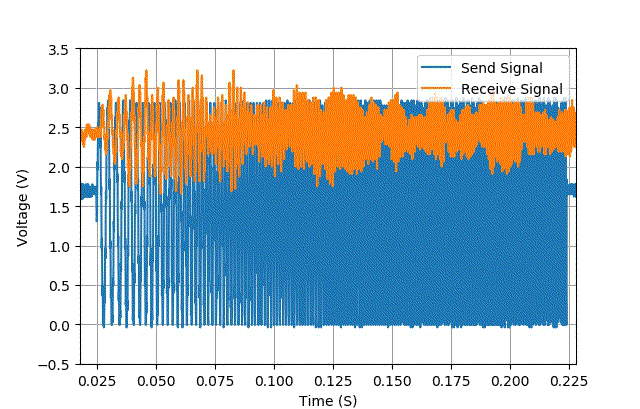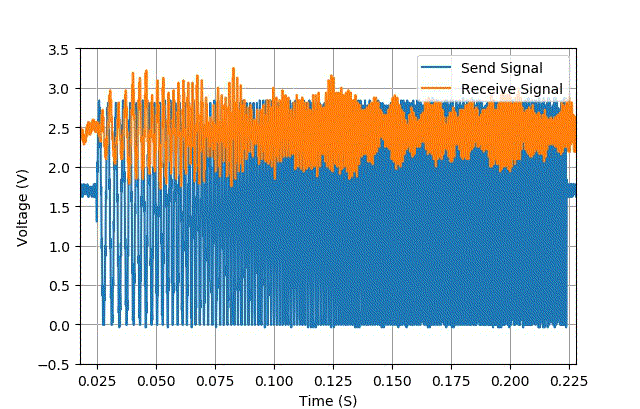
▲ 图2.2.1 . 发送的Chirp信号与接收到的Chirp信号

2.2.2 实验要求

  在 Chirp信号公式与对离散生成算法之间的差异 给出了生成 Chirp 信号生成的方法，请按照如下指标生成 Chirp 信号数据：

• 采样频率： $f_s=10kHz$ ；
• 起始频率： $f_{start}=250Hz$ ；
• 停止视频： $f_{stop}=2000Hz$ ；
• 采集数据长度： $N=2048$ ；

  对数据添加 $\left[-1,1\right]$ 之间的均匀分布的随机噪声， 形成两个带有噪声的 Chirp 信号。 计算它们之间的互相关信号。

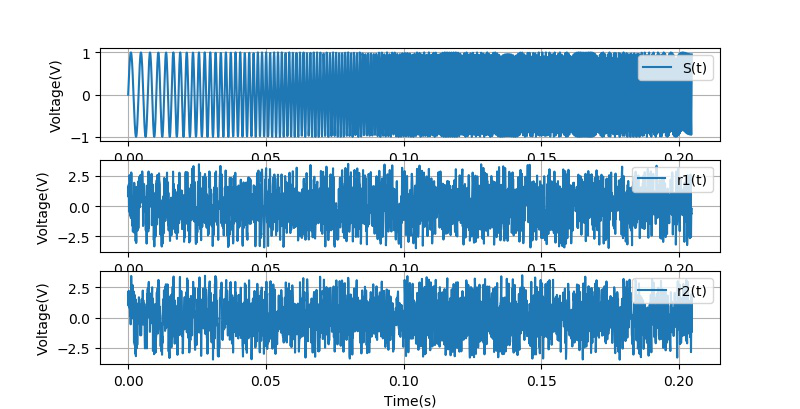
▲ 图2.2.2 . Chirp 信号与对应的两个增加有随机信号Chirp信号

  下面是两个带有很大噪声的 Chirp 信号之间互相关的结果。

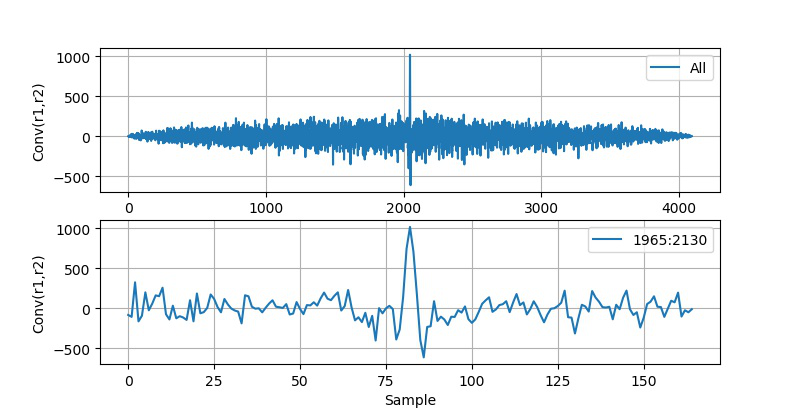
▲ 图2.2.3 .两个叠加有随机噪声的Chirp信号互相关结果 上：全部的互相关结果；下：将互相关结果中心展开

---

■ 相关文献链接:

• 室外声音信标可行性分析
• Chirp信号公式与对离散生成算法之间的差异

● 相关图表链接:

• 图2.2.1 . 发送的Chirp信号与接收到的Chirp信号
• 图2.2.2 . Chirp 信号与对应的两个增加有随机信号Chirp信号