立体视觉入门指南（1）：坐标系与相机参数

亲爱的同学们，我们的世界是3D世界，我们的双眼能够观测三维信息，帮助我们感知距离，导航避障，从而翱翔于天地之间。而当今世界是智能化的世界，我们的科学家们探索各种机器智能技术，让机器能够拥有人类的三维感知能力，并希望在速度和精度上超越人类，比如自动驾驶导航中的定位导航，无人机的自动避障，测量仪中的三维扫描等，都是高智机器智能技术在3D视觉上的具体实现。

立体视觉是三维重建领域的重要方向，它模拟人眼结构用双相机模拟双目，以透视投影、三角测量为基础，通过逻辑复杂的同名点搜索算法，恢复场景中的三维信息。它的应用十分之广泛，自动驾驶、导航避障、文物重建、人脸识别等诸多高科技应用都有它关键的身影。

本课程将带大家由浅入深的了解立体视觉的理论与实践知识。我们会从坐标系讲到相机标定，从被动式立体讲到主动式立体，甚至可能从深度恢复讲到网格构建与处理，感兴趣的同学们，来和我一起探索立体视觉的魅力吧！

本课程是电子资源，所以行文并不会有太多条条框框的约束，但会以逻辑清晰、浅显易懂为目标，水平有限，若有不足之处，还请不吝赐教！
个人微信：EthanYs6，加我申请进技术交流群 StereoV3D，一起技术畅聊。
CSDN搜索 ：Ethan Li 李迎松，查看网页版课程。
随课代码，将上传至github上，地址：StereoV3DCode：https://github.com/ethan-li-coding/StereoV3DCode

针孔模型Pinhole mode

在科学研究中，一个现象内部的过程总是复杂而难以清晰看透，而聪明的学者们总会用最简单的模型去做初始描述，提出一个相对简单的模型。成像过程亦不例外，他们将三维世界中的坐标点映射到二维图像平面的过程用一个几何模型进行描述，这个模型有很多种，其中最简单的称为针孔模型。

针孔成像的原理大家都学过，现实世界中源于某个物体的光线穿过针孔，会在底板上投影成一幅倒立的图像。如图1所示：

图1 针孔模型1

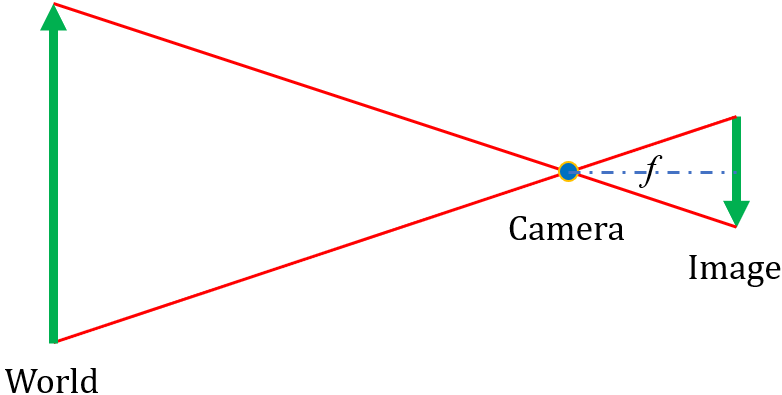
将针孔模型对应到成像过程中，现实世界的物体即为三维空间的成像目标，针孔为摄像机中心，倒影成像平面则为二维影像平面。如图二（左）所示，我们用简单的线条来绘制这样的关系，摄像机中心到成像平面之间的距离我们称之为焦距$f$。但是倒立的成像总感觉别扭，因此转换一下，将成像平面拿到相机前方来，保持焦距为$f$，由成像过程可知，图像此时不再是倒立的了，解放了大家的脖子，见图2（右）所示。

图2 针孔模型2

从针孔模型中，我们可以找到一个特征，那就是现实世界的任一点、其在成像平面上的投影点、相机中心在一条直线上，这种特征称为中心投影或者透视投影，也是做成像分析的基础。透视投影将三维空间投影到二维平面上，是一种降秩空间透射变换（三维空间降成了二维空间）。

坐标系简介

通过针孔模型，我们了解了成像过程，似乎非常简单，但它此时只是一张图片，给你感官上的理解，要基于它完成复杂的3D测量，必须借用那一连串噼里啪啦让人又爱又恨的数学公式，而公式建立的基础，就是一个个坐标系，具体来说，是一个个笛卡尔坐标系。如果你不知道什么是笛卡尔坐标系，我想你也不会点开我的博客看到这里，所以介绍就此略过。

我认为你们已经掌握了一个前提知识：立体视觉的三个关键坐标系是影像坐标系、相机坐标系、世界坐标系。如果没有，那我就强塞给你这个概念。

影像坐标系

影像坐标系是一个二维坐标系，是在影像内建立的坐标系，描述像素点在影像中的位置，分为以像素为单位的$(u,v)$坐标系以及以物理尺寸为单位的$(x,y)$坐标系。在计算机视觉中，$(u,v)$坐标系以左上角位置为原点，$u$轴和$v$轴分别平行于图像平面的两条垂直边（$u$轴朝右，$v$轴朝下），如图3左所示；$(x,y)$坐标系以像主点$(u_0,v_0)$为原点，$x$轴和$y$轴分别与$u$轴和$v$轴平行且方向一致，如图3右所示。

图3 影像坐标系

上面提到像主点，特别说明一下，它是摄影中心到成像平面的垂点，它是一个非常重要的点位。

如果我们知道像素到物理尺寸的转换关系，即一个像素的物理尺寸，也就是像元尺寸为$dx\ast dy$（$x$方向尺寸为$dx$，$y$方向尺寸为$dy$），就可以在两类坐标系之间相互转换：
$$\begin{array}{rl}u-u_0& =x/d_x\\ v-v_0& =y/d_y\end{array}$$

为了便于矩阵运算，我们会写成矩阵形式：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{d_x}& 0& u_0\\ 0& \frac{1}{d_y}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

公式两边的三维矢量是一种齐次表达方式，即把第三维设置为1来用三维矢量表示二维矢量，这样做的好处是可以用矩阵运算的方式完成三维到二维的变换。为什么要做这个转换呢？是因为$xy$坐标系和相机坐标系的紧密联系，同学们往后看。

相机坐标系

相机坐标系是一个三维空间坐标系，是非常关键的一个坐标系，它承担着建立影像坐标系和世界坐标系之间联系的重任。所以前人们在建立相机坐标系时，有一个很关键的考量是如何能更好的把影像坐标系和世界坐标系之间联系起来。

两个三维坐标系（相机和世界）之间的转换用旋转和平移就可以方便表达，重点是三维的相机坐标系和二维的影像坐标系之间如何更好转换。方案是这样的：相机坐标系的原点在相机中心，$XY$轴和影像$xy$坐标系的$xy$轴平行，$Z$轴垂直于像平面且朝向像平面，$Z$轴和像平面的交点正是影像$xy$坐标系的原点（像主点）。如图4所示。

图4 相机坐标系

在此方案下，像平面上的所有像素点在相机坐标系下的$Z$坐标等于焦距$f$，$XY$坐标和影像$xy$坐标系下的值相等，即若像素点$p$在影像$xy$坐标系下的坐标为$(x,y)$，则其在相机坐标系下的坐标为$(x,y,f)$。

根据中心投影的特征，假设像素点$p$是空间点$P$的投影点，那么如何建立两兄弟之间的坐标关系呢？

图5 相机坐标系2

我们假设像素$p$对应的空间点在相机坐标系下的坐标为$(X_c,Y_c,Z_c)$（下标c是camera的意思）。若两点位于从坐标系原点发出的同一条直线上，那么他们的坐标有什么关系？答案是等比例关系。即
$$\frac{x}{X_c}=\frac{y}{Y_c}=\frac{f}{Z_c}$$

为了便于矩阵运算，我们会写成矩阵形式：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{f}{Z_c}& 0& 0\\ 0& \frac{f}{Z_c}& 0\\ 0& 0& \frac{1}{Z_c}\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

还记得上一节，我们把$xy$坐标系转换成$uv$坐标系，结合上式，便可以把相机坐标系转换成$uv$坐标系，即
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{d_x}& 0& u_0\\ 0& \frac{1}{d_y}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\frac{f}{Z_c}& 0& 0\\ 0& \frac{f}{Z_c}& 0\\ 0& 0& \frac{1}{Z_c}\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\frac{1}{Z_c}\left[\begin{array}{ccc}\frac{f}{d_x}& 0& u_0\\ 0& \frac{f}{d_y}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

通常把$Z_c$称为尺度因子$\lambda$，把中间的3x3矩阵叫做内参矩阵$K$，显然内参矩阵$K$描述的是相机坐标系到$uv$坐标系的转换关系。简单的表达式如下
$$\lambda p=K{P}_c$$

内参矩阵

内参矩阵$K$是相机的关键参数之一，$\frac{f}{d_x}$和$\frac{f}{d_y}$实际是将以物理尺寸为单位的焦距$f$转换成像素为单位的焦距值，记$f_x=\frac{f}{d_x}$，$f_y=\frac{f}{d_y}$，$f_x$和$f_y$分别是焦距在两个像元方向上的像素单位值。最终得到内参的矩阵表达：
$$K=\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]$$

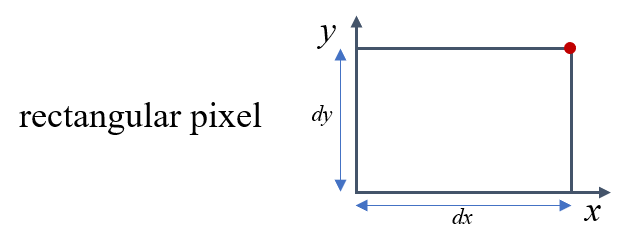
额外需要了解的一点是，由于制造工艺的偏差，像素不是绝对的矩形（图6左），而是一个平行四边形（图6右）。

图6 倾斜像素

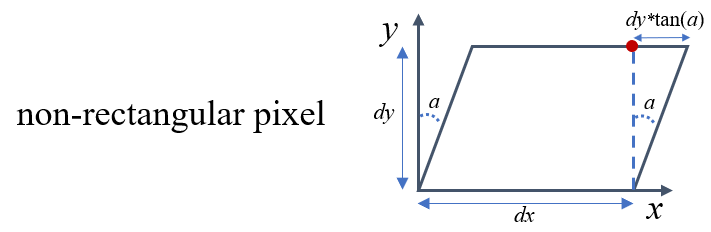
这时候像素的纵向边界和$y$轴并不平行而是倾斜一定的角度，于是在$K$矩阵中引入一个倾斜因子$s$（实际上可以推导$s=f_{x}tan(a)$，这里就不展开了，感兴趣的可以查资料自己推导下），此时$K$矩阵表示为
$$K=\left[\begin{array}{ccc}{f}_x& s& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]$$

最后相机坐标到$uv$坐标的转换公式为：
$$\lambda \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& s& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

世界坐标系

世界坐标系是一个固定的三维坐标系，是一个绝对坐标系，它旨在将空间中的所有点都统一到同一个坐标系下表达，在不同的应用场景中，世界坐标系的定义并不一样，比如大地测量中，将水准原点当做世界坐标系的原点；在相机标定中，将标定板的某个角点作为世界坐标系。

图7 世界坐标系

世界坐标系和相机坐标系都是三维坐标系，它们之间可以用旋转平移来做转换

图8 坐标系之间的旋转平移

假设空间点P在世界坐标系中的坐标为$(X_w,Y_w,Z_w)$，则可以通过一个3x3的单位正交旋转矩阵 $R$ 和3x1的平移矢量 $t$ 来转换成相机坐标系坐标$(X_c,Y_c,Z_c)$：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R_{3\times 3}\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+t_{3\times 1}$$

或者写成另一种形式：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{cc}{R}_{3\times 3}& t_{3\times 1}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

我们把旋转矩阵 $R$ 和平移矢量 $t$ 称为相机的外参矩阵。

外参矩阵

外参矩阵也是相机的关键参数之一，由一个3x3的单位正交旋转矩阵 $R$ 和3x1的平移矢量 $t$ 组成，它们描述的是世界坐标系到相机坐标系之间的转换关系。需要提一点的是，在不同学科中外参矩阵会有一些定义区别，比如在摄影测量学科中，将相机坐标系转换到世界坐标系的旋转矩阵 $R$ 以及摄影中心在世界坐标系中的位置 $C$ 作为外参。它们目的一致，都是为了描述相机和世界坐标系之间的转换关系。

同样用一个简单表达式来描述世界坐标系到相机坐标系的变换：
$$P_c=\left[\begin{array}{cc}R& t\end{array}\right]\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$

投影矩阵

虽然我们花很多篇幅介绍了相机坐标系，但是在实践过程中，最直接接触的却是影像$uv$坐标系和世界坐标系，在影像三维重建中，通常前者是输入，后者是输出，所以将世界坐标系转换成$uv$坐标系是很关键的转换。

上文已经得到了世界到相机，相机到$uv$的转换公式，因此世界到$uv$并没有什么难度：
$$\lambda \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& s& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}{R}_{3\times 3}& t_{3\times 1}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

世界坐标系到影像坐标系的转换实际上表达的是透视投影中空间点到像点的投影关系，所以把该转换矩阵叫做投影矩阵$M$，通过矩阵运算可知投影矩阵是一个3x4的矩阵，它是内参矩阵和外参矩阵的乘积。

同样用一个简单表达式来表达这种转换：
$$\lambda p=K\left[\begin{array}{cc}R& t\end{array}\right]\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]=M\left[\begin{array}{c}{P}_w\\ 1\end{array}\right],M=K\left[\begin{array}{cc}R& t\end{array}\right]$$

总结

本节我们通过针孔模型引入以透视投影为基本原理的相机成像模型，并对一切公式推导的源头：三大坐标系（影像/相机/世界） 做了详细的介绍，在深入了解坐标系的过程中，几类关键的相机参数（内参/外参）也缓缓而出。用图示加公式推导，让大家直观且有逻辑性的掌握这方面的知识，希望能够给入门的同学一些帮助，下一节我们再见。

练习作业

这里为大家准备了一些练习题，可以通过实践加深理解：

练习：写一个Camera类（基于Eigen库 ），用内参矩阵K、旋转矩阵R、平移矩阵t（或相机中心C）来构造
实现接口：

1. 世界坐标系到相机坐标系的转换 W2C
2. 相机坐标系到世界坐标系的转换 C2W
3. 相机坐标系到图像坐标系的转换 C2I
4. 世界坐标系到图像坐标系的转换 W2I
5. 有深度作为参数，图像坐标系到相机坐标系的转换I2C
6. 有深度作为参数，图像坐标系到世界坐标系的转换I2W

参考答案地址：https://github.com/ethan-li-coding/StereoV3DCode