前言

二维图像能提供丰富的环境信息或空间信息，这些信息涵盖（1）图像上每一点的亮度与物体某个表面点的反射光的强度的关系（2）图像点在图像平面上的位置与 $a .$ 相机与空间物体的相对方位的关系； $b .$ 相机的内部结构关系¹。利用这些信息，可实现诸如测距，测量，识别，地图构建，定位，相机运动和姿态估计等方面的工作。

为了描述相机的几何成像关系，需要进行数学建模，这些几何模型参数就是相机参数，包括内参和外参，而求解参数的过程就称为相机标定。本文所介绍的相机模型是计算机视觉中广泛使用的针孔模型（The basic pinhole model）。这种模型在数学上是三维空间到二维平面（image plane or focal plane）的中心投影，由一个 $3\times4$ 投影矩阵 $P = K [R ∣ t]$ ²来描述， $K$ 为相机内参（internal camera parameters）， $[R ∣ t]$ 为外参（external parameters）。

我们通过描述四个坐标系的相互转换关系，可以拆分和剖析投影矩阵 $P$ 。

四个坐标系

下图表示四个坐标系的相互关系³。
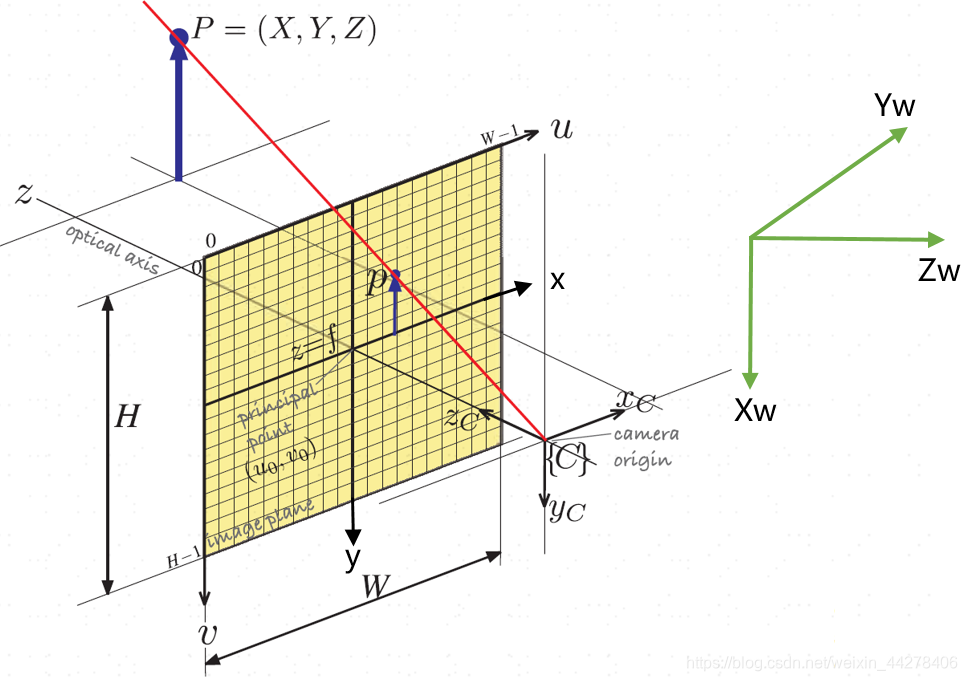
在这里插入图片描述

图像像素坐标系：表示三维空间物体在图像平面上的投影，像素是离散化的，其坐标原点在CCD图像平面的左上角， $u$ 轴平行于CCD平面水平向右， $v$ 轴垂直于 $u$ 轴向下，坐标使用 $(u, v)$ 来表示。图像宽度 $W$ ，高度 $H$
图像物理坐标系：坐标原点在CCD图像平面的中心， $x, y$ 轴分别平行于图像像素坐标系的 $(u, v)$ 轴，坐标用 $(x, y)$ 表示。
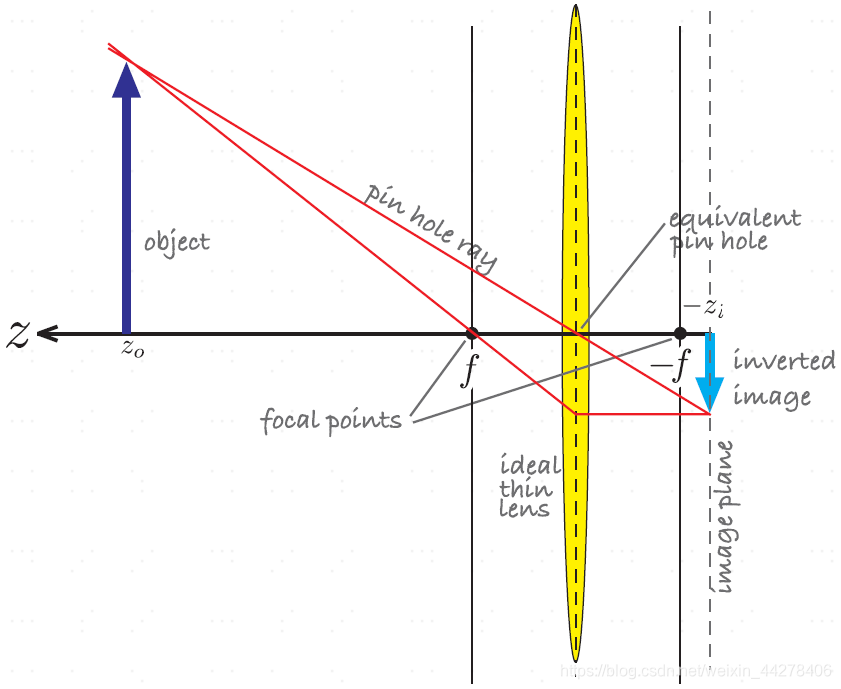
相机坐标系：以相机的光心为坐标系原点， $X_c,Y_c$ 轴平行于图像坐标系的 $x, y$ 轴，相机的光轴为 $Z_c$ 轴，坐标系满足右手法则。相机的光心可理解为相机透镜的几何中心，如下图所示³。
世界坐标系：用于表示空间物体的绝对坐标，使用 $X_w,Y_w,Z_w)$ 表示，世界坐标系可通过旋转和平移得到相机坐标系。

世界坐标系-相机坐标系

刚体变换只改变物体的空间位置(平移)和朝向(旋转)，而不改变其形状的变换，可用两个变量来描述：正交单位旋转矩阵 $R$ ，三维平移矢量 $t$ 。世界坐标系到相机坐标系的转换关系也是如此，如下图所示²。
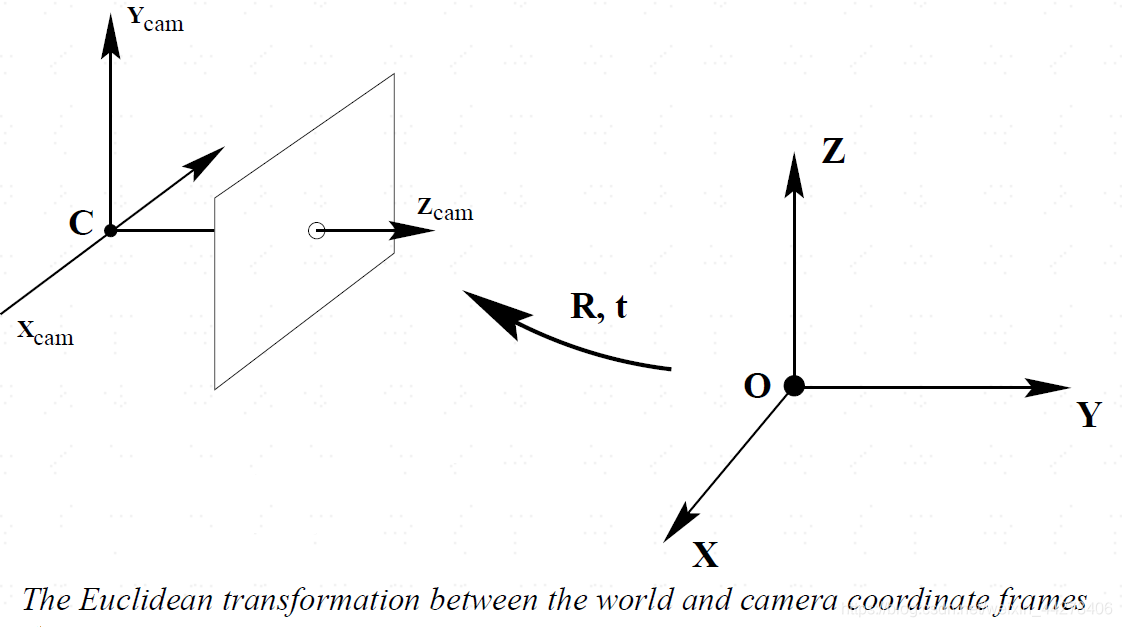
在这里插入图片描述
平移比较好理解，世界坐标系原点移动到相机坐标系；旋转一共有三个自由度，即绕 $x, y, z$ 旋转，根据旋转角度可以分别得三个方向上的旋转矩阵 $R_x,R_y,R_z$ ，而旋转矩阵即为他们的乘积⁴， $R=R_x \times R_y \times R_z$ 。以绕 $X$ 轴旋转为例，我们可以得到 $R_x$ 。
在这里插入图片描述
$\left\{ \begin{aligned} X_C &= X_W \\ Y_C &= Y_W * \cos{\theta} + Z_W * \sin{\theta} \\ Z_C &= -Y_W * \sin{\theta} + Z_W * \cos{\theta} \end{aligned} \right.$
写成矩阵形式如下，
$\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \end{array} \right ]= \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos{\theta} & \sin{\theta} \\ 0 & -\sin{\theta}& \cos{\theta} \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]= R_x \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]$
同理可得绕 $y$ 轴和 $z$ 轴旋转的关系。
$\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \end{array} \right ]= \left[ \begin{array}{ccc} \cos{\theta} & 0 & -\sin{\theta} \\ 0 & 1 & 0 \\ \sin{\theta} & 0& \cos{\theta} \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]= R_y \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]$
$\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \end{array} \right ]= \left[ \begin{array}{ccc} \cos{\theta} & \sin{\theta} & 0 \\ -\sin{\theta} & \cos{\theta} & 0 \\ 0 & 0& 1 \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]= R_z \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ]$
于是可得旋转矩阵 $R = R_x R_y R_z$
$\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \end{array} \right ]= R \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \end{array} \right ] + t$
写成齐次坐标系形式为，
$\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \\ 1 \end{array} \right ]= \left[ \begin{array}{cc} R & t\\ 0_{1 \times 3} & 1 \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right ] \tag{1}$

相机坐标系-图像坐标系

相机坐标系到图像坐标系是透视关系，利用相似三角形进行计算²。
在这里插入图片描述
$\left\{ \begin{aligned} \frac{x}{f} = \frac{X_C}{Z_C} \\ \frac{y}{f} = \frac{Y_C}{Z_C} \end{aligned} \right.$
写成齐次坐标形式的矩阵相乘为，
$Z_C\left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right ]= \left[ \begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right ] \left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \\ 1 \end{array} \right ] = [K|0]\left[ \begin{array}{c} X_C \\ Y_C \\ Z_C \\ 1 \end{array} \right ] \tag{2}$
其中 $K$ 称为相机内参数矩阵。

主点偏离图像中心(principal point offset)¹：在实际应用中，由于事先不知道主点的确切位置，通常都是以图像中心或者图像的左上角作为图像坐标系的原点来建立图像坐标系的。当主点不是坐标系原点时，相机内参数矩阵形式如下。 $\left[ \begin{array}{ccc} f & 0 & x_0 \\ 0 & f & y_0 \\ 0 & 0 & 1 \end{array} \right ]$
这种说法可能不太好理解，我们这里仅作参考，感兴趣的可以阅读Reference1和2中的相关章节。

图像坐标系-像素坐标系

像素坐标系是图像坐标系的离散化表示，实际CCD相机每个像素对应一个感光点，是个矩形，假设其物理尺寸为 $d x$ 宽， $d y$ 高。以CCD传感器的左上角为坐标原点建立的坐标系与以成像平面中心建立的坐标系的转换关系如下。
在这里插入图片描述
$\left\{ \begin{aligned} u = \frac{x}{d_x} + u_0 \\ v = \frac{y}{d_y} + v_0 \end{aligned} \right.$
齐次坐标矩阵形式为，
$\left[ \begin{array}{c} u \\ v \\ 1 \end{array} \right ]= \left[ \begin{array}{ccc} \frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \end{array} \right ] \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right ] \tag{3}$

由于制造工艺的限制，一般情况下，CCD 摄像机数字离散化后的像素不是一个矩形而是一个平行四边形，四边形的一边平行于 $u$ 轴，而另一边与 $u$ 轴形成一个 $\theta$ 角。则内参矩阵中会出现一个扭曲因子 $s$ 。感兴趣可进一步阅读Reference1中相关章节。

综合

根据公式 $(1) (2) (3)$ 可得，
$Z_C\left[ \begin{array}{c} u \\ v \\ 1 \end{array} \right ]= \left[ \begin{array}{ccc} \frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \end{array} \right ] \left[ \begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right ] \left[ \begin{array}{cc} R & t\\ \bf{0}_{1 \times 3} & 1 \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right ] \\ = \left[ \begin{array}{cccc} f_x & 0 & u_0 & 0 \\ 0 & f_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right ] \left[ \begin{array}{cc} R & t\\ \bf{0}_{1 \times 3} & 1 \end{array} \right ] \left[ \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right ]$
其中，
$\left[ \begin{array}{cccc} f_x & 0 & u_0 & 0 \\ 0 & f_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right ]$ 为相机内参矩阵， $\left[ \begin{array}{cc} R & t\\ \bf{0}_{1 \times 3} & 1 \end{array} \right ]$ 为外参矩阵。相机标定就是为了求解这两个矩阵的参数。

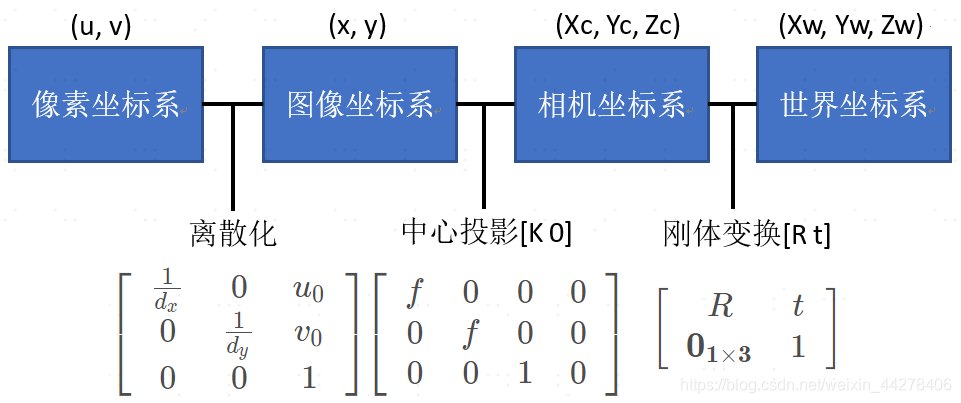
一图胜千言

在这里插入图片描述

扫描二维码关注公众号，回复： 12333725 查看本文章

Reference

吴福朝. 计算机视觉中的数学方法[M]. 科学出版社, 2008 ↩︎ ↩︎
Hartley, R., & Zisserman, A. (2004). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511811685 ↩︎ ↩︎ ↩︎
Corke P. Robotics, vision and control: fundamental algorithms in MATLAB® second, completely revised[M]. Springer, 2017. ↩︎ ↩︎
Rotation of Axes ↩︎

相机标定（1）——四个坐标系

前言