对动态规划思想的理解
文章目录
一、概述
动态规划,最核心的就是动态转移方程,这个动态转移方程想要表达的意思说白了就当前状态和前一个状态有关,换句话说,当前的状态与之前的状态有关,或者是当前状态是根据之前已经有的状态“转移”过来的。
这里还有一个难点,就是状态如何定义的问题,一般来说,这个状态与多个其他的状态有关。听起来是不是很抽象,下面我们来看看几个例子
二、通过问题来发掘共同点
01背包问题——引出问题
这种问题,相信这种问题大家一定并不陌生了,但是本篇文章的重点不是去解题,而是通过几道动态规划的题来阐述一下动态规划的特征以及今后如何去做动态规划的题。
我们先来看一下动态规划问题的dp数组是如何定义的:
dp[i][j] = max(dp[i-1][j] + dp[i-1][j-weight]) // 意思就是在第i个物品选和不选两种情况里选一个最大值
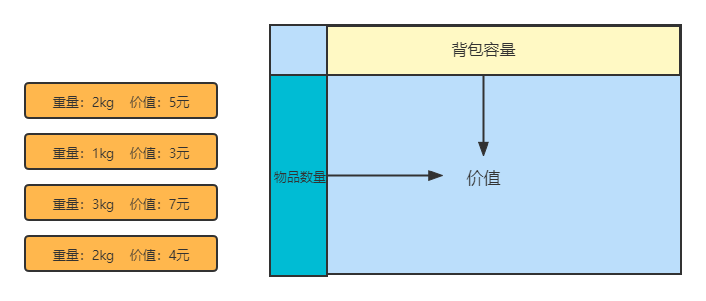
根据图图中的二维数组可以知道i表示物品的数量,j表示背包的容量。
很多人在看别人题解的时候都能够听懂别人的解题思路,也能理解为什么这样写。但是当自己独自去写这类题目的时候就很难受了,死活想不出来,最难想的就是dp[i][j]中的i和j分别代表什么意思。
我在这里说一下我个人的见解:
仔细观察图片中的行和列,就会发现他们都是一维的,例如【背包容量】是[0,maxWeight],【物品数量】是[0,maxNum],而在这个问题中【价值】是二维的,它受到物品数量和背包容量两个因素的影响。
通常来说,动态规划的问题中对于每一步,都需要面临类似于【选与不选/向左还是向下】这种【二选一】,并且我们想要求得的值一般都会受到两个因素的影响,其中任何一个因素发生改变,都可能会让这个结果也发生改变。因此,通常来说,dp[i][j]的值就是我们【想要求得的结果】,而行和列则是影响着这个结果的两个维度,通常是一维的,也可以理解为是有一个确定范围的维度。
而为什么物品的种类和价值我们不作为状态来考虑呢?因为他们是不变的,某一个物品的重量和价值已经是固定的了,不会去影响其别的属性。所以我在图中也吧这两个属性单独画在一起
总结一下:动态规划题目特征【二选一】(两种情况选一种),定义行和列,通常是一维的属性,如【数量】,对于dp[i][j]数组中的值
LeetCode 494.目标和——印证
题目:
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例:
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
题解:
根据之前的猜想,我们现在现在利用这道题来印证一下之前的想法是否正确
为什么说这个是动态规划的题呢?因为从题目中我们很明显可以感觉到【二选一】,一个数要么是正的要么是负的,是不是很符合我们之前说的特征。
接下来就是确定一下我们【想要的结果】是什么,很明显,题目中要我们输出的是【方法个数】,接下来就要分析一下这个【方法个数】受到哪两个【一维因素】的影响,首先第一个就是【数字的个数i】,范围是[0,nums.length],第二个就是【前i个数的和j】,范围是[-sum,+sum]。
现在验证一下这样是否符合我们前面说的,【想要的结果】收到两个【一维因素】的影响。当可选的数的数量发生改变的时候,方法种数肯定也会发生变化,这个毋庸置疑,如果【前i个数的和】发生改变,那么方法种数肯定也会发生变化的。经过验证发现没有问题。
接下来最后一步,动态转移方程推导。有了前面的基础之后,我们只需要进行推导就可以了,如果推导过程发现不对劲,再回过头去看看前面的步骤就可以发现问题。有可能是【一维因素】选的不合适。现在,我们开始推导动态转移方程:
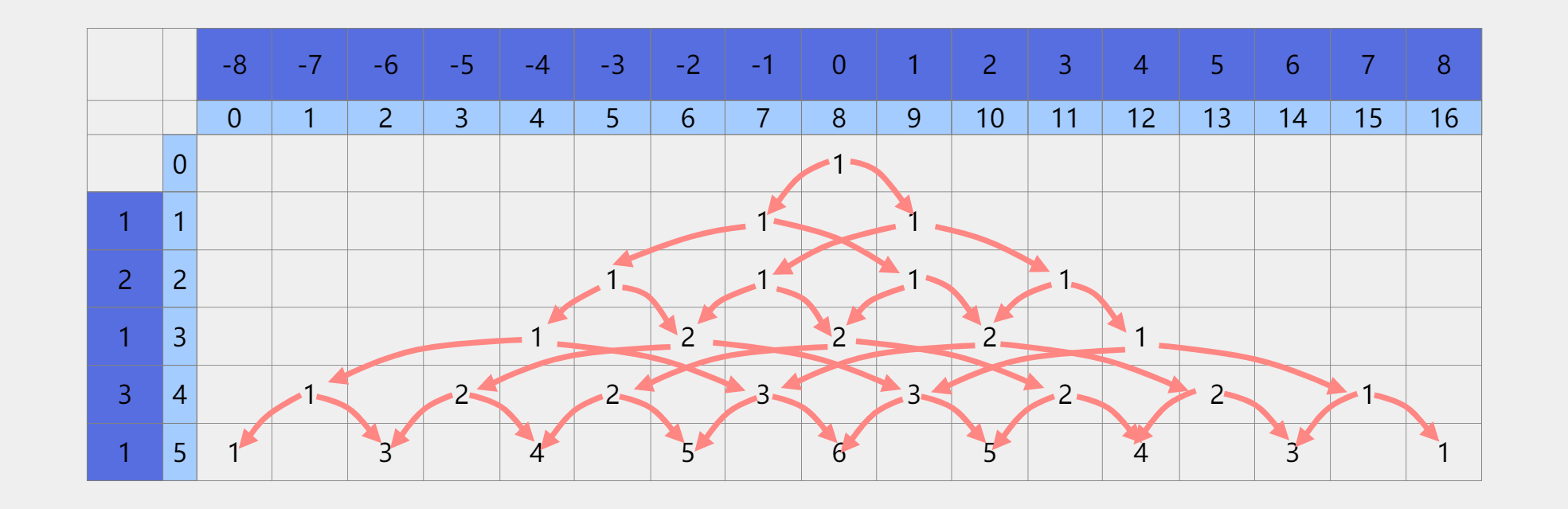
上图是leetCode某题解的一个图,为了方便理解动态转移方程,我就拿过用了。
因为对于一个数,要么为正,要么为负
我们在进选择之前肯定是有一个起点的,这个起点就是可以选择的数是0个的时候,这个时候的总和为0,对应到数组中就是dp[0][8] = 1,表示0个数的时候,和为0,只有一种方法。
接下来我们遇到了第一个数:1,我们可以选择正的或者负的,就可以根据dp[0][8] = 1得到dp[1][7] = dp[1][7] + 1和dp[1][9] = dp[1][9] + 1;由此往下以此类推就会得到所有可能的情况,这里一定要自己去推敲一下。
由此,我们得到了【动态转移方程】: 逐层往下,一直dp[i][j]可以推导出dp[i+1][j+num[i]] = dp[i+1][j+num[i]] + dp[i][j],dp[i+1][j-num[i]] = dp[i+1][j-num[i]] + dp[i][j](这里的num[i]就是下一行要进行选择的数)
然后我们只【需要的结果】就是dp[nums.length][target + 8]
这里只展示动态转移方程那部分的代码:
for (int row = 0; row < nums.length; row++) {
for (int col = 0; col < dp[row].length; col++) {
if (dp[row][col]!=0){
dp[ row + 1 ][ col - nums[row] ] += dp[row][col];
dp[ row + 1 ][ col + nums[row] ] += dp[row][col];
}
}
}
另一种思路:
上述思路是最容易想到的一种,还有一种比这种要巧妙一点,但是会更难想一点,说白了就是把问题从哪些是正哪些是负变成了选哪些数组合成和为x ,这就变成了选与不选的问题了,但是这个需要一点点的推导,只要所有数的绝对值之和与目标target(所有正数和负数之和)确定了,就可以得到正数的和,从而我们只需要解决选前i个数组成和为x的方法个数。
以题目中的例一为例,数的总和为5时,target为3,我们只需要知道让正数只和为4的组合数就可以。这理解不展开说这个了
三、总结
今天主要讲解了一下动态规划问题的特征、以及动态转移方程是如何得来的,还有就是在遇到这类问题时该如何去思考解题方案。以后有机会再说说关于动态规划二维数组优化成一位数组的方法。
如果对本篇文章的内容有疑惑或者不明白的地方欢迎留言,看到会及时回复的