布尔运算是逻辑门的基础,逻辑门和布尔代数的定律构成了数字电路的基础。本文的目的是对布尔表达式进行化简,化简的目的是在实际电路中使用更少的逻辑门。一个逻辑电路有三种表达方式,分别是布尔表达式,真值表,以及卡诺图。真值表最直观,卡诺图适合化简,布尔表达式适合运算。布尔表达式,真值表,卡诺图相互之间可以转换。
思维导图

布尔运算
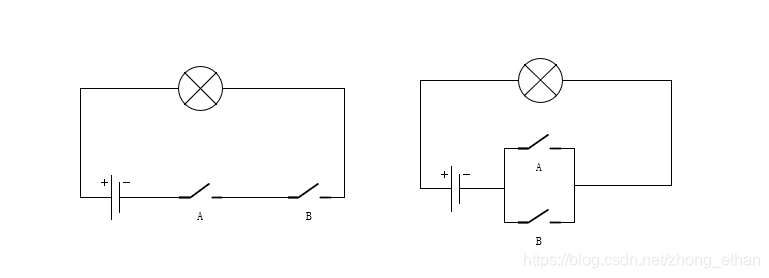
先看一个小例子:图左为开关串联电路,只有在开关A和B都同时闭合的情况下,小灯泡才会亮;图右为开关并联电路,当开关A和开关B至少有一个闭合时,小灯泡就会亮,这种逻辑关系成为布尔运算。布尔运算是一切逻辑的本质。
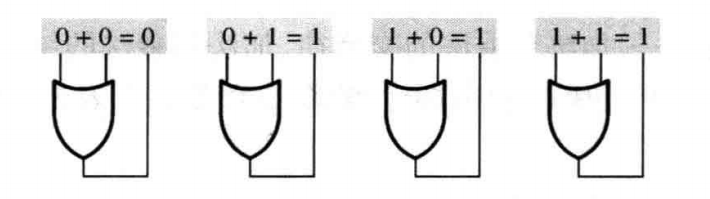
布尔加法
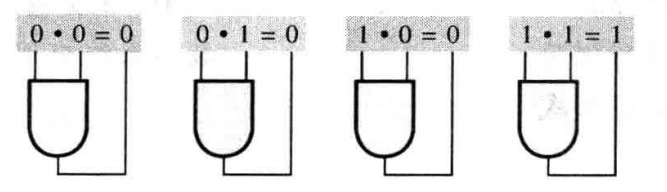
布尔乘法
布尔非运算
0 ˉ = 1 \bar{0}=1 0ˉ=1
1 ˉ = 0 \bar{1}=0 1ˉ=0
布尔代数定律
交换律 A +B = B + A AB=BA
结合律 (A+ B)+C=A+(B+C) (AB)C=A(BC)
分配律 A(B+C)=AB+BC
好不夸张的说,掌握了布尔运算与布尔代数定律就掌握了数字电路。因为接下来所有的逻辑化简必须遵从以上两点。
布尔代数常用基本法则
| 一 | 二 |
|---|---|
| A + 0 = A A+0=A A+0=A | A + 1 = 1 A+1=1 A+1=1 |
| A ⋅ 0 = 0 A·0=0 A⋅0=0 | A ⋅ 1 = A A·1=A A⋅1=A |
| A + A = A A+A=A A+A=A | A + A ˉ = 1 A+\bar{A}=1 A+Aˉ=1 |
| A . A = A A.A=A A.A=A | A . A ˉ = 0 A.\bar{A}=0 A.Aˉ=0 |
| A ˉ ˉ = A \bar{\bar{A}}=A Aˉˉ=A | A + A B = A A+AB=A A+AB=A |
| A + A ˉ B = A + B A+\bar{A}B = A+B A+AˉB=A+B | ( A + B ) ( A + C ) = A + B C (A+B)(A+C)=A+BC (A+B)(A+C)=A+BC |
推导 ① A + A B = A ( 1 + B ) = A A+AB=A(1+B)=A A+AB=A(1+B)=A
推导 ② A + A ˉ B = A + A B + A ˉ B = A + ( A + A ˉ ) B = A + B A+\bar{A}B=A+AB+\bar{A}B=A+(A+\bar{A})B=A+B A+AˉB=A+AB+AˉB=A+(A+Aˉ)B=A+B
推导 ③ ( A + B ) ( A + C ) = A A + A C + A B + B C = A + A C + A B + B C = A + A B + B C = A + B C (A+B)(A+C)=AA+AC+AB+BC=A+AC+AB+BC=A+AB+BC=A+BC (A+B)(A+C)=AA+AC+AB+BC=A+AC+AB+BC=A+AB+BC=A+BC
狄摩根定理
狄摩根第一定理: X Y ˉ = X ˉ + Y ˉ \bar{XY}=\bar{X}+\bar{Y} XYˉ=Xˉ+Yˉ
狄摩根第二定理: ( X + Y ) ˉ = X ˉ Y ˉ \bar{(X+Y)}=\bar{X}\bar{Y} (X+Y)ˉ=XˉYˉ
狄摩根定理的意义在于将与运算和或运算联系在一起
布尔表达式的标准形式
由于狄摩根定理的存在,任何与运算都可以转换成或运算,任何或运算都可以转成与运算。任何布尔表达式都可以有以下两种标准形式。
乘积项之和一个布尔表达式用一个或门及两个或者更多的与门实现,形如 A B + B C AB+BC AB+BC。
和项之乘积一个布尔表达式用一个与门及两个或者更多的或门实现,形如 ( A + B ) ( B + C ) (A+B)(B+C) (A+B)(B+C)。
布尔表达式的域 一般布尔表达式的域是指该表达式所有变量的集合可以是原码或者反码的形式。例如 A B + B C AB+BC AB+BC的域是{A、B、C}。
最小项(标准乘积项)之和表达式的每个乘积项都包含该表达式域中的所有变量。
如何把乘积项之和转换成标准乘积项之和?利用法则 A + A ˉ = 1 A+\bar{A}=1 A+Aˉ=1和 A . 1 = A A.1=A A.1=A将非标准项中没有包含的变量与该乘积项进行与运算,这样就产生两个标准乘积项。例如乘积项 A B AB AB缺少变量 C C C, A B ( C + C ˉ ) = A B C + A B C ˉ AB(C+\bar{C})=ABC+AB\bar{C} AB(C+Cˉ)=ABC+ABCˉ。
最大项(标准和项)之积表达式的每个和项都包含该表达式域中的所有变量。
如何把和项之积转成标准和项之积?需要用到三个法则,一是 A . A ˉ = 0 A.\bar{A}=0 A.Aˉ=0,二是 A + B C = ( A + B ) ( A + C ) A+BC=(A+B)(A+C) A+BC=(A+B)(A+C),三是 A + 0 = A A+0=A A+0=A。将非标准项中没有包含的变量与该和项进行或运算,这样就产生两个标准和项。例如 A + B = A + B + C . C ˉ = ( A + B + C ) ( A + B + C ˉ ) A+B=A+B+C.\bar{C}=(A+B+C)(A+B+\bar{C}) A+B=A+B+C.Cˉ=(A+B+C)(A+B+Cˉ)。通过这种方法,可以把所有的非标准和项转成标准和项。
最小项之和与最大项之积互相转换非常简单,只需要狄摩根定理就可以。
**最小项之和和最大项之积意义?**可以快速的得到布尔表达式的真值表和进行布尔表达式化简
布尔表达式和真值表
最小项之和转换成真值表 对于域中有 n n n个变量的表达式,真值表中最多可以产生 2 n 2^{n} 2n种组合。乘积项之和表达式中至少有一个乘积项为1时,表达式的结果就为1。共有哪几种组合结果可以为1,取决于最小项之和表达式中有几项乘积项。
最小项之和表达式为 A ˉ B ˉ C + A B ˉ C ˉ + A B C \bar{A}\bar{B}C+A\bar{B}\bar{C}+ABC AˉBˉC+ABˉCˉ+ABC。该域中有三个变量,真值表中只有八种组合。根据最小项之和表达式,只有三种组合的结果为1,分别是001,100和111。得到的真值表如下:
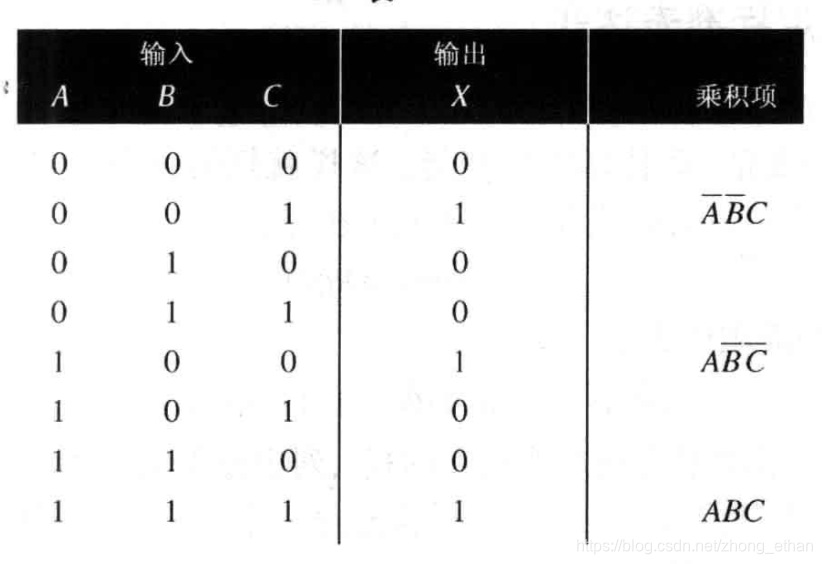 最大项之积转成真值表 和项乘积表达式中只要有一项和项为0,表达式的结果就为0。因此,只要确定每个和项为0的条件就可以得出真值表。
最大项之积转成真值表 和项乘积表达式中只要有一项和项为0,表达式的结果就为0。因此,只要确定每个和项为0的条件就可以得出真值表。
和项之积表达式为 ( A + B + C ) ( A + B ˉ + C ) ( A + B ˉ + C ˉ ) ( A ˉ + B + C ˉ ) ( A ˉ + B ˉ + C ) (A+B+C)(A+\bar{B}+C)(A+\bar{B}+\bar{C})(\bar{A}+B+\bar{C})(\bar{A}+\bar{B}+C) (A+B+C)(A+Bˉ+C)(A+Bˉ+Cˉ)(Aˉ+B+Cˉ)(Aˉ+Bˉ+C)。在ABC分别为000,010,011,101和110时,表达式的结果为0。因此得到如下真值表:
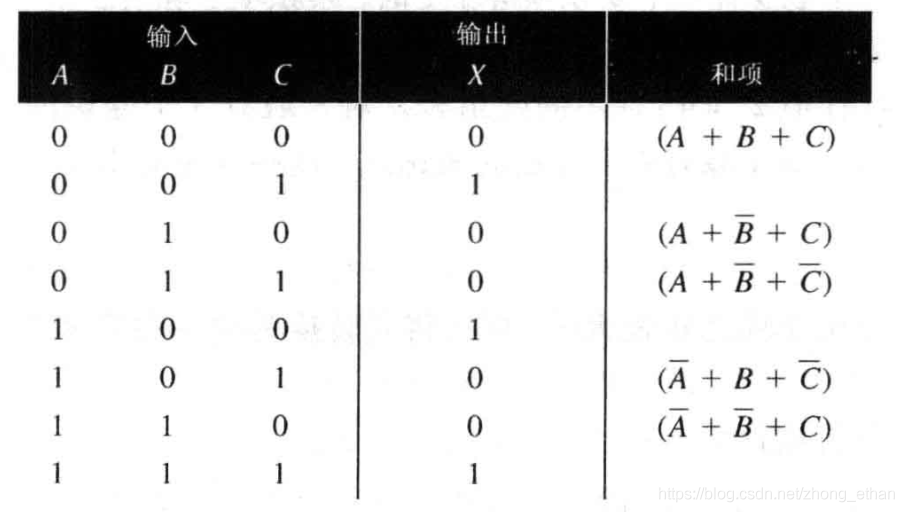
真值表转换成最小项之和或最大项之积非常简单,只要将上面两个过程反过来就可以。
卡诺图
卡诺图的作用是化简布尔表达式,只要出现形如 A B C + A B C ˉ ABC+AB\bar{C} ABC+ABCˉ的组合,就把 C C C消去。就像消消乐一样。
三变量卡诺图
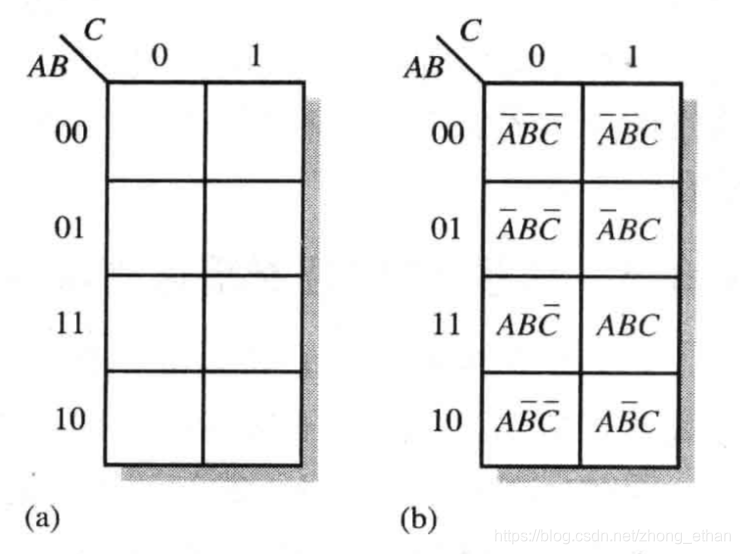 四变量卡诺图
四变量卡诺图
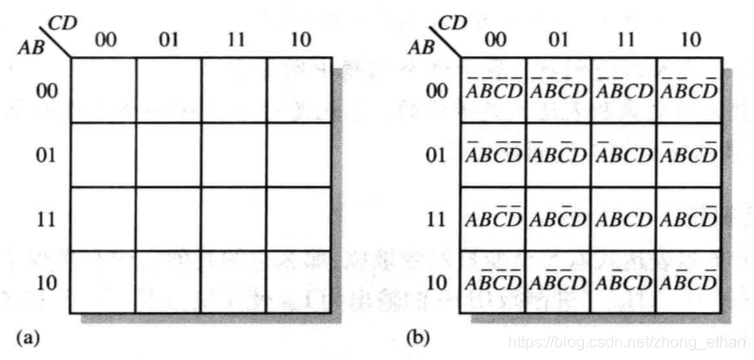 五变量卡诺图
五变量卡诺图
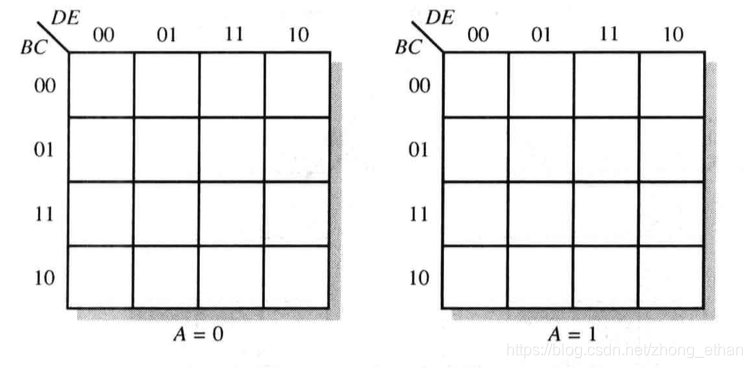
观察卡诺图的横轴和纵轴,会发现变量是按照00,01,11,10形式排列的,这么做的好处是易于化简,采用的准则是 A + A ˉ = 1 A+\bar{A}=1 A+Aˉ=1。例如 A B C + A B C ˉ ABC+AB\bar{C} ABC+ABCˉ可以化简为 A B ( C + C ˉ ) AB(C+\bar{C}) AB(C+Cˉ)。两个乘积项在卡诺图中处在相邻的两个小方块中。
最小项之和的卡诺图映射
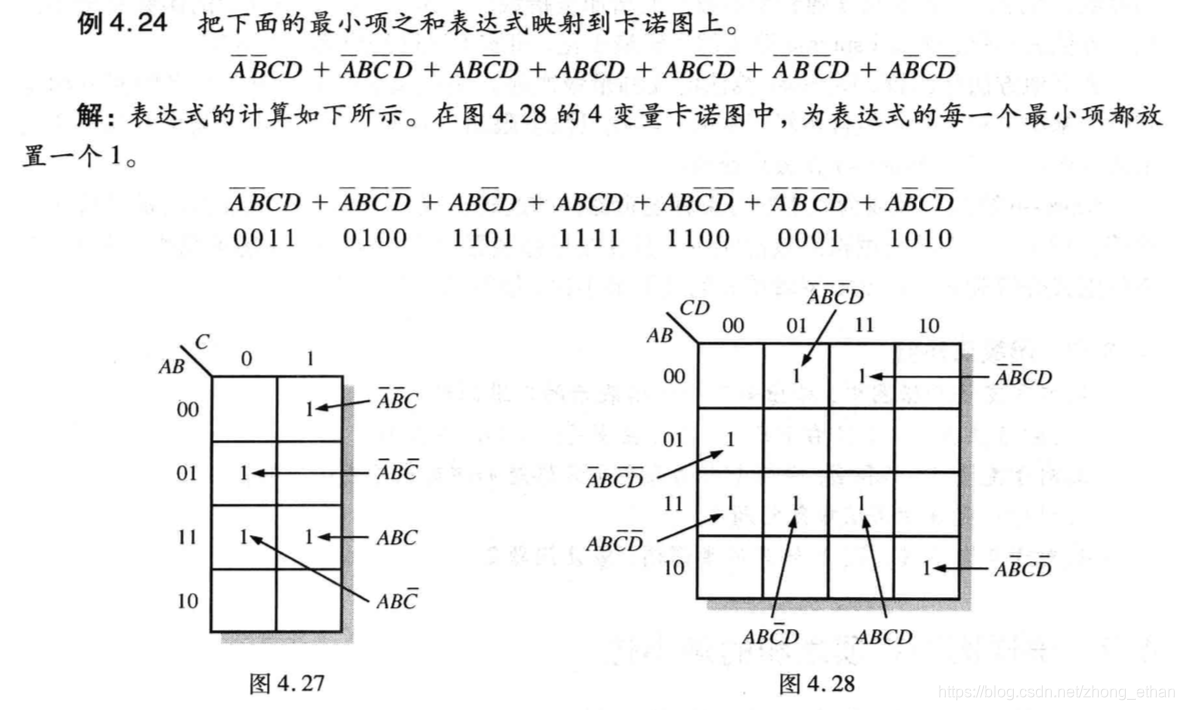 对于一些无效的组合,即在实际情况中并不会发生的变量组合,在卡诺图上可以当成无关项来处理。无关项可以是0也可以是1,用X来表示。
对于一些无效的组合,即在实际情况中并不会发生的变量组合,在卡诺图上可以当成无关项来处理。无关项可以是0也可以是1,用X来表示。
卡诺图化简
化简的基本目的是:圈尽可能的大, 组尽可能的小
1、一个小组只能含 2 n 2^{n} 2n个小方格,1、2、4、8、16等。必须是2的幂次方。
2、小组中的小方格必须与相同组内一个或多个小方格相邻,并允许跨边界。但小组中的所有小方格不一定互相连接;
3、卡诺图中的每个标1的小方格必须包含在至少一个组内。允许小组内小方格重叠
对于有无关项的卡诺图,可以将无关项当成1以获得一个最大的组,也可以当成0。组越大,得到的乘积项越简单。