机器学习基础学习-逻辑回归

1、逻辑回归基本概念

在之前的线性回归当中，f(xi)是我们的预测值
在逻辑回归中，我们得到的这个y值本质上是一个概率，所以用p来表示，然后进而通过p进行分类得到最后的结果（这里相当于多做了一步操作，得到了分类的结果）
如果这里不进行根据p的值进行分类的操作，那么它就是一个回归算法，计算的是我们通过样本的特征来拟合计算出一个事件发生的概率（例如我们通过一个病人的信息来计算出他患有恶性肿瘤的概率）。
ps：逻辑回归一般用来解决二分类问题，对于多分类问题，逻辑回归本身是不支持的（但是可以通过一些技巧进行改进来解决多分类问题，这一块博主还没看过怎么玩）

对于概率而言，他的值域是在[0,1]，而线性回归当中，值域是从负无穷到正无穷的，没有值域的限制，我们得到的结果可信程度是比较低的

这里的做法是将线性回归之后的结果，再次作为特征值进行运算，将其结果的值域转换到[0,1] （转换过程见下图）

这里的表达方式不同的地方有不同的说法，思想是一致的，这里的Sigmoid函数可以非常好的将对应的函数值转换成概率值

下面我们对Sigmoid函数进行绘制

# sigmoid函数绘制
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(t):
  return 1 / (1 + np.exp(-t))

x = np.linspace(-10, 10, 500) #x在-10到10选取500个点
y = sigmoid(x)

plt.plot(x, y)
plt.show()

接下来把之前得到的y值带入到sigmoid函数当中

这里附上另一个版本的，总体思想是一致的

2、逻辑回归的损失函数

所以对于损失函数，我们引入了下面的内容

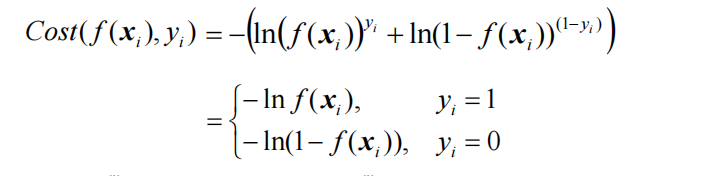
（1）真实样本标记为1的时候（损失函数为-log( p )）
当p取0的时候，损失函数-log( p )趋近于正无穷，这是因为当p取0的时候，我们按照之前的分类方式，会把这个样本分类成0这一类，但是这个样本实际的值是1这一类，显然分类错误了，所以这时的损失函数是正无穷的。随着p逐渐增大，我们的损失逐渐减小。
当p到达1的时候，根据分类标准，我们会把样本分类为1的这一类，此时这个分类和我们的真实的分类y=1是一致的，此时我们的损失函数-log( p )取0，也就是没有任何损失。


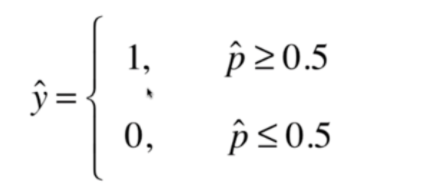
（2）真实样本标记为0的时候（损失函数为-log(1-p)）


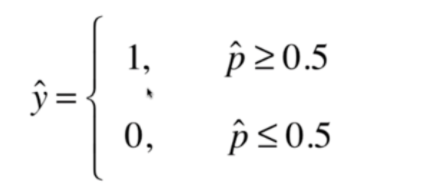
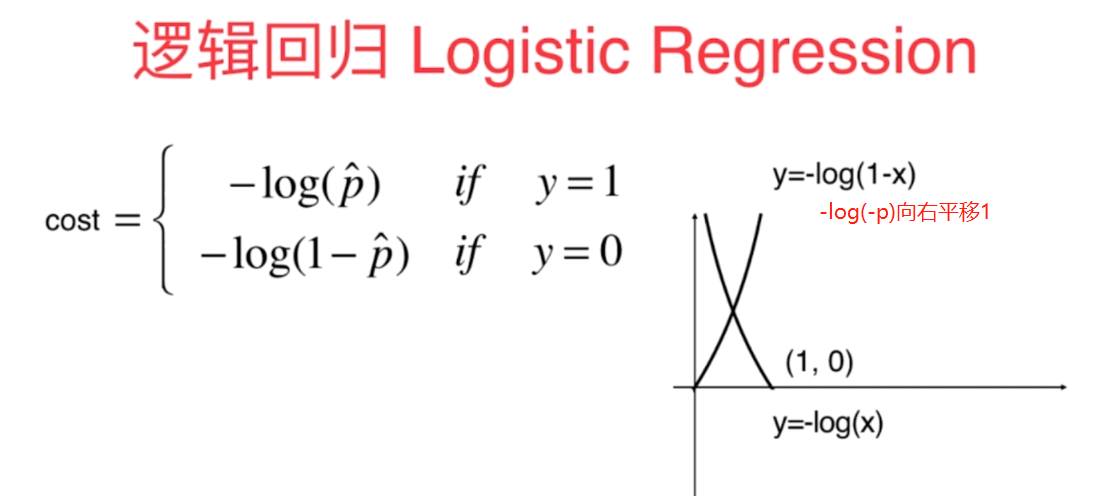
这里的-log(1-p)实际是-log(-p)向右平移1，为了p的取值在[0,1]之间，否则-log(-p)的曲线只会无限逼近y轴
当我们的p取1的时候，损失函数-log(1-p)趋近于正无穷，这是因为当我们的p等于1的时候，按照之前的分类方式，这个样本会被分类到1的分类中，但是y的实际值为0 ，所以这里的损失函数是正无穷，随着p逐渐减小，损失函数也逐渐减小。
当p=0的时候，此时这个样本是分类到0，而我们的真值也是0，所以此时分类是正确的，这种情况下的损失为0。
损失函数的要求就是预测结果与真实结果越相近，函数值越小。当y=0时，1-p的概率会比较大，在前面加上负号，Cost值就会很小；当y=1时，p的概率会比较大，在前面加上负号，Cost值就会很小。综上，Cost值越大,代表我们要对本次错判负责任越大,Cost值越趋近于零，说明我们的预测值和真实值的结果更加接近。
合并损失函数
显然，我们根据y=0或者y=1来对损失函数进行分类实际上是比较麻烦的，所以我们可以把损失函数进行合并

合并之后的函数和之前的分类函数其实是等价的（这里可以带入0,1的情况发现其实是和分类下的情况是一致的）
将所有样本的损失加在一起后（下图多了一个求平均值的过程，显然不求平均值的话，样本越多则损失函数越大，这显然是不合理的）


进一步进行替换后

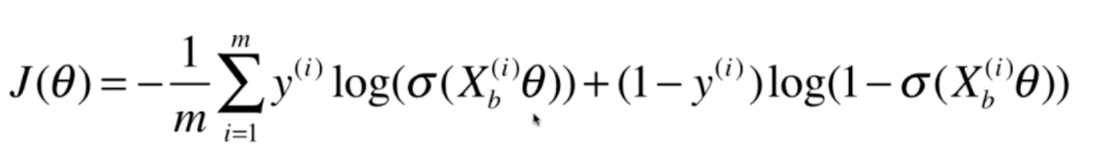
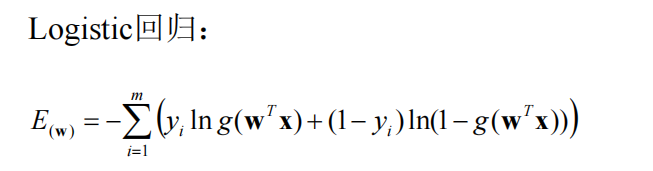
求得损失函数之后，我们要做的就是找到一个theta使我们的损失函数达到最小值（这里求最小值不能再像之前的线性回归一样，可以直接求得数学的解析解，但是我们可以用梯度下降法求得最小值，这里的损失函数仍然是一个凸函数，是不存在局部最优解的，只有一个唯一的全局最优解，因此不用担心梯度下降法要求得多次。）

3、逻辑回归损失函数的梯度

这里实际上是一个数学推导的过程，这里跳过推导过程，直接上公式

4、数据集

数据集采用的sklearn的鸢尾花数据集，其中共有三组150个数据，每个数据代表一株鸢尾花，其包含4个属性，即一株鸢尾花的花萼长度，花萼宽度，花瓣长度，花瓣宽度。
iris.data为一个150行4列的矩阵，存储鸢尾花的属性信息。
iris.target为一个长为150的一维数组，数组中第n个值为0/1/2表示第n个数据代表的鸢尾花属于Setosa，Versicolour，Virginica）三个种类
这里我们进行实际使用的时候，先把数据集做成只有两种分类（一共是100个数据，我们采取其中的75个数据进行训练，剩下25个数据进行测试），并且我们只取了其两个特征，方便后面我们处理决策边界后能更好的可视化。

5、实现逻辑回归算法

这部分代码可以套用我前面两篇博客的部分算法然后进行修改。
（1）sigmoid函数

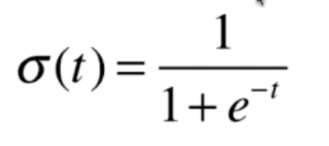
  # 定义私有sigmoid函数
  def _sigmoid(self, t):
    return 1. / 1. + np.exp(-t)

这里调用这个方法的时候遇到了一个数据溢出的问题。解决方法

def _sigmoid(self, x):
    l=len(x)
    y=[]
    for i in range(l):
      if x[i]>=0:
        y.append(1.0/(1+np.exp(-x[i])))
      else:
        y.append(np.exp(x[i])/(np.exp(x[i])+1))
    return y

（2）y_hat，或者说概率

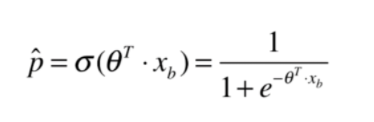
y_hat = self._sigmoid(X_b.dot(theta))

（3）损失函数

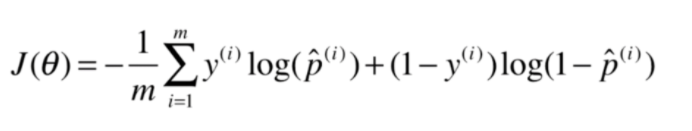
-np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)

（4）求梯度

这里求梯度其实和上篇博客当中线性回归求梯度差不多，区别在于把X_b.dot(theta)的过程套上sigmoid函数。

X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)

（5）梯度下降求解theta过程

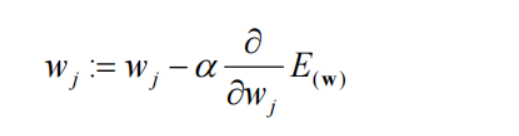
这里完全套用多元线性回归的梯度下降解法

    # 梯度下降求解theta矩阵
    def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
      theta = initial_theta
      cur_iters = 0

      while cur_iters < n_iters:
          gradient = dJ(theta, X_b, y) # 求梯度
          last_theta = theta # theta重新赋值前，记录上一场的值
          theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
          # 最近两点的损失函数差值小于一定精度，退出循环
          if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
              break
          cur_iters += 1
      return theta

（6）通过梯度下降过程进行训练

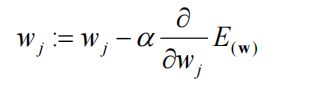
  def fit(self, X_train, y_train, eta = 0.01, n_iters = 1e4): 
    # 根据训练数据集X_train, y_ .train训练logistics Regression模型
    # X_train的样本数量和y_train的标记数量应该是一致的
    # 使用shape[0]读取矩阵第一维度的长度，在这里就是列数
    assert X_train.shape[0] == y_train.shape[0], \
    "the size of x_ .train must be equal to the size of y_ train"
    # 损失函数
    def J(theta, X_b, y):
      y_hat = self._sigmoid(X_b.dot(theta))
      try:
        return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
      except:
        return float('inf') # 返回float最大值

    # 梯度(比较笨的方法)
    def dJ(theta, X_b, y):
      return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)


    # 梯度下降求解theta矩阵
    def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
      theta = initial_theta
      cur_iters = 0

      while cur_iters < n_iters:
          gradient = dJ(theta, X_b, y) # 求梯度
          last_theta = theta # theta重新赋值前，记录上一场的值
          theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
          # 最近两点的损失函数差值小于一定精度，退出循环
          if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
              break
          cur_iters += 1
      return theta

    # 得到X_b
    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    initial_theta = np.zeros(X_b.shape[1]) # 设置n+1维的向量,X_b.shape[1]:第一行的维数
    # X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
    # 获取theta
    self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

    self.interception_ = self._theta[0] # 截距
    self.coef_ = self._theta[1:] # 系数 
    return self

下面是预测过程，主要通过测试数据对我们的训练结果进行验证
（7）X_b

X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])

（8）预测概率结果

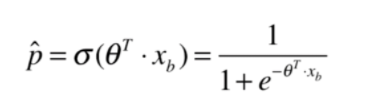
self._sigmoid(X_b.dot(self._theta))

（9）对概率进行分类

def predict(self, X_predict):
    # 给定待预测数据集X_predict,返回表示X_predict的结果向量
    prob = self.predict_prob(X_predict) # prob向量存储的都是0-1的浮点数
    # 进行分类(布尔类型强制转换为整型)
    # return np.array(prob >= 0.5, dtype='int')
    l = len(prob)
    temp_prob=[]
    for i in range(l):
      if prob[i] >= 0.5:
        temp_prob.append(1)
      else:
        temp_prob.append(0)
    return temp_prob

（10）调用sklearn的预测精确度方法

  '''
    预测准确度
  '''
  def score(self, X_test, y_test):
    # 根据测试数据集 X_test 和y_test 确定当前模型的准确度
    y_predict = self.predict(X_test)
    return accuracy_score(y_test, y_predict)

（11）整体代码

# 逻辑回归问题；在多元线性回归问题的基础上进行修改
# 逻辑回归问题；在多元线性回归问题的基础上进行修改
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score


class logisticsRegression:
  def __init__(self):
      # 初始化logistics Regression模型
      self.coef_ = None # 系数，对应theta1-n，对应的向量
      self.interception_ = None # 截距，对应theta0
      self._theta = None # 定义私有变量，整体计算的theta

  # sigmoid函数数据溢出问题：https://blog.csdn.net/wofanzheng/article/details/103976889
  # 定义私有sigmoid函数
  # def _sigmoid(self, t):
  #   return 1. / 1. + np.exp(-t)

  def _sigmoid(self, x):
    l=len(x)
    y=[]
    for i in range(l):
      if x[i]>=0:
        y.append(1.0/(1+np.exp(-x[i])))
      else:
        y.append(np.exp(x[i])/(np.exp(x[i])+1))
    return y

  '''
    梯度下降
  '''
  def fit(self, X_train, y_train, eta = 5.0, n_iters = 1e4): 
    # 根据训练数据集X_train, y_ .train训练logistics Regression模型
    # X_train的样本数量和y_train的标记数量应该是一致的
    # 使用shape[0]读取矩阵第一维度的长度，在这里就是列数
    assert X_train.shape[0] == y_train.shape[0], \
    "the size of x_ .train must be equal to the size of y_ train"
    # 损失函数
    def J(theta, X_b, y):
      y_hat = self._sigmoid(X_b.dot(theta))
      try:
        return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
      except:
        return float('inf') # 返回float最大值

    # 梯度(比较笨的方法)
    def dJ(theta, X_b, y):
      return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)


    # 梯度下降求解theta矩阵
    def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
      theta = initial_theta
      cur_iters = 0

      while cur_iters < n_iters:
          gradient = dJ(theta, X_b, y) # 求梯度
          last_theta = theta # theta重新赋值前，记录上一场的值
          theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
          # 最近两点的损失函数差值小于一定精度，退出循环
          if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
              break
          cur_iters += 1
      return theta

    # 得到X_b
    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    initial_theta = np.zeros(X_b.shape[1]) # 设置n+1维的向量,X_b.shape[1]:第一行的维数
    # X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
    # 获取theta
    self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

    self.interception_ = self._theta[0] # 截距
    self.coef_ = self._theta[1:] # 系数 
    return self

  '''
    预测可能性的过程
  '''
  def predict_prob(self, X_predict):
    # 给定待预测数据集X_predict,返回表示X_predict的结果概率向量
    X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
    return self._sigmoid(X_b.dot(self._theta))


  '''
    预测过程
  '''
  def predict(self, X_predict):
    # 给定待预测数据集X_predict,返回表示X_predict的结果向量
    prob = self.predict_prob(X_predict) # prob向量存储的都是0-1的浮点数
    # 进行分类(布尔类型强制转换为整型)
    # return np.array(prob >= 0.5, dtype='int')
    l = len(prob)
    temp_prob=[]
    for i in range(l):
      if prob[i] >= 0.5:
        temp_prob.append(1)
      else:
        temp_prob.append(0)
    return temp_prob

  '''
    预测准确度
  '''
  def score(self, X_test, y_test):
    # 根据测试数据集 X_test 和y_test 确定当前模型的准确度
    y_predict = self.predict(X_test)
    return accuracy_score(y_test, y_predict)

  '''
    显示属性
  '''
  def __repr__(self):
      return "logisticsRegression()"



# 这里先用鸢尾花数据集（150行4列：150个样本，4个特征值）
iris = datasets.load_iris()

X = iris.data
y = iris.target

# 这里鸢尾花数据集有三种分类，我们先把数据集做成只有两种分类
X = X[y < 2, :2] # 取前两个特征方便可视化
y = y[y < 2]

# print('X', X.shape)
# print('y', y.shape)

# 绘制y=0、y=1相应的x的两个特征在二维平面的坐标,[y == 行范围, 列范围]
# X[y == 0, 1]：获取y==0的行，然后获取这些行的第二个元素
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

# 训练
# X_train = X[y < 2, :2] # 取前两个特征方便可视化
# y_train = y[y < 2]
# 实例化
log_reg = logisticsRegression()
# 分离测试集与数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
# print('X_train', X_train)
# print('X_test', X_test)
# print('y_train', y_train)
# print('y_test', y_test)


# 进行训练,通过测试训练分离的方法测试逻辑回归的结果
log_reg.fit(X_train, y_train) # logisticsRegression()
# 得到预测值
print('预测值', log_reg.score(X_test, y_test))
# log_reg.predict_prob(X_test)
print('X_test概率值', log_reg.predict_prob(X_test))
print('通过概率划分得到的分类值', log_reg.predict(X_test))
print('y_test测试值', y_test)

# 绘制决策边界的直线(全数据集)
x1_plot = np.linspace(4, 8, 1000)
x2_plot = (-log_reg.coef_[0] * x1_plot - log_reg.interception_) / log_reg.coef_[1]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.plot(x1_plot, x2_plot)
plt.show()

# 绘制决策边界的直线(测试数据集)
x1_plot = np.linspace(4, 8, 1000)
x2_plot = (-log_reg.coef_[0] * x1_plot - log_reg.interception_) / log_reg.coef_[1]
plt.scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1], color = "orange")
plt.scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1], color = "pink")
plt.plot(x1_plot, x2_plot)
plt.show()

# 绘制决策边界的直线(训练数据集)
# x1_plot = np.linspace(4, 8, 1000)
# x2_plot = (-log_reg.coef_[0] * x1_plot - log_reg.interception_) / log_reg.coef_[1]
# plt.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], color = "orange")
# plt.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], color = "pink")
# plt.plot(x1_plot, x2_plot)
# plt.show()

运行结果
我通过train_test_split分出了25%的数据作为测试值

对于X数组的每一个元素，都有一个预测的概率值，概率值越趋近于1，逻辑回归算法越愿意分类为1.概率值越趋近于0，逻辑回归算法越愿意分类为0。
对比我们的概率、通过概率划分得到的分类值、测试值

精确度 1.0
X_test概率值 [0.9227936051194328, 0.9519259109675121, 0.044313407612935944, 0.7245094894872708, 0.015037803596307778, 0.9360128868584877, 0.9071547662200364, 0.13470801322828907, 0.03001244120537637, 0.016621389485626907, 0.9852022132977879, 0.0045245545109356255, 0.12344004945195731, 0.8671844914321338, 0.9071547662200364, 0.044313407612935944, 0.975709242178656, 0.059032167089442714, 0.9152639352134383, 0.980045275612995, 0.9910023165927783, 0.006120665765293931, 0.9640335726611468, 0.9986686902634397, 0.04433374163271295]

通过概率划分得到的分类值 [1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0]

y_test测试值 [1 1 0 1 0 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0]

针对以上结果，可以看到首先我们根据概率进行划分的分类值取值正确，其次我们的分类值和原数据集给出的分类值是一致的，所以我们通过梯度下降的方法进行逻辑回归实验成功。

6、决策边界

决策边界顾名思义是作为我们数据分类的边界而产生出的概念，针对我们之前的概念，其实决策边界就是我们针对概率值进行分类的时候的一个临界值，直观来说就是能够把样本正确分类的一条边界。


通过决策边界其实我们可以绘制出一条分类边界的直线

现在的横纵坐标都代表着特征。我们以x1特征为横轴，x2特征为纵轴，通过我们之前求得的系数和截距就可以绘制出决策边界的一条直线。

# 绘制决策边界的直线
x1_plot = np.linspace(4, 8, 1000)
x2_plot = (-log_reg.coef_[0] * x1_plot - log_reg.interception_) / log_reg.coef_[1]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.plot(x1_plot, x2_plot)
plt.show()

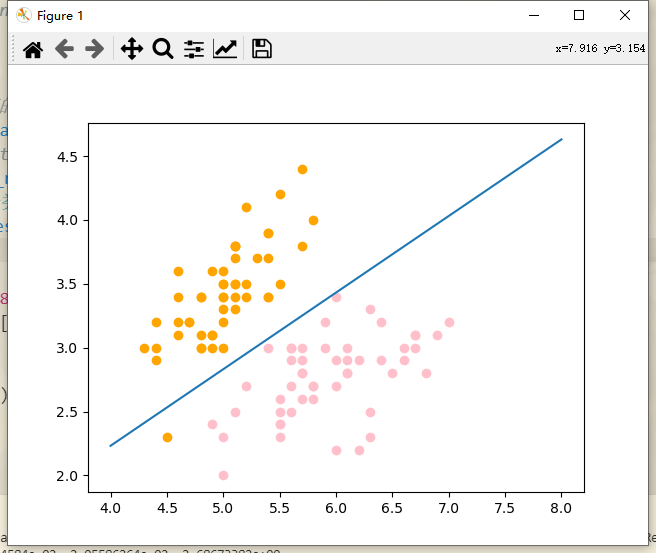
可以看到我们的决策边界大体上将样本分为了两类，如果我们新来一个样本，我们将这个样本的每个特征和theta相乘，如果大于等于0，我们给他分类为1，相反小于零则分类为0。如果等于0 就落在了决策边界上（无论分类为0或者1都是正确的）。

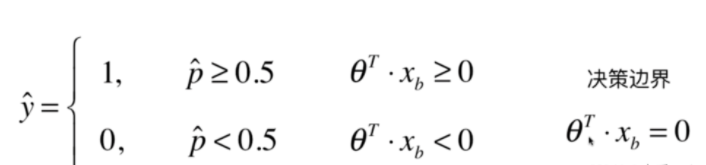
但是这里有一个橘色的点分类在了另一侧，这是分类错误的情况，但是之前通过打印的数据，我们可以看到测试的结果正确率实际上是100%。所以这个点应该是出现在训练数据集当中，所以接下来我们针对测试集进行绘图

发现这个分类是完全正确的。
接下来看训练数据集的部分

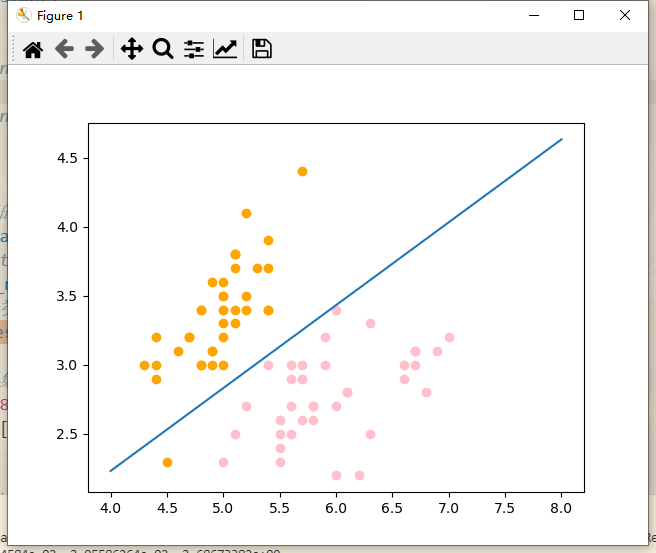
这一块出错果然是出现在训练数据集当中，考虑两方面的原因
（1）训练次数不够，加大训练次数到1e5

加大训练次数到1e6

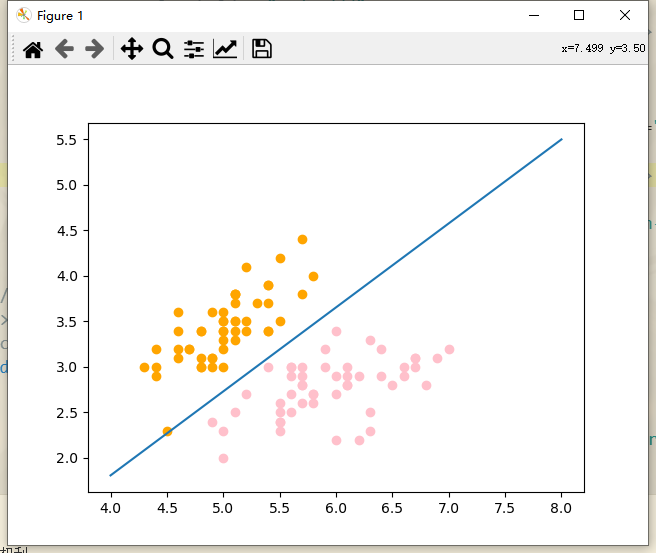
（2）修改学习率
训练次数不变，增大学习率到0.5

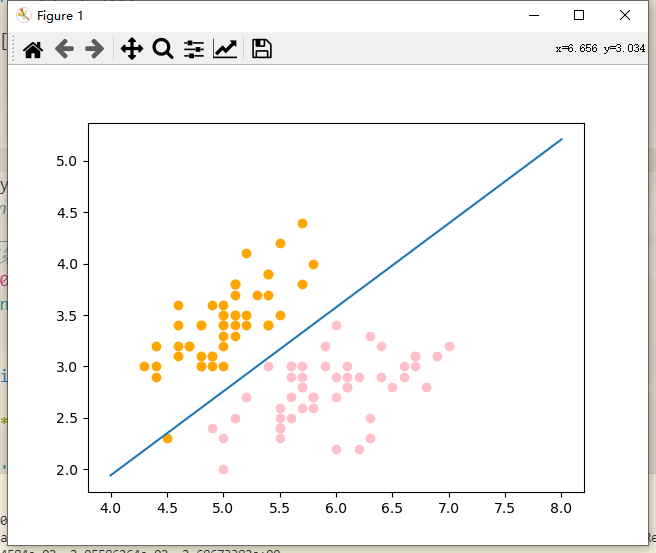
增大学习率到2.5


其实这个现象主要是因为我们的损失函数在学习率为0.01的时候完全没有收敛，在这种情况下来考虑剩下的步骤是不对的。
一开始设置的学习率太小了，训练次数再多，其实变化也不是很大，这个时候我们改变学习率到合适的值，首先让收敛函数收敛才能再进行分析