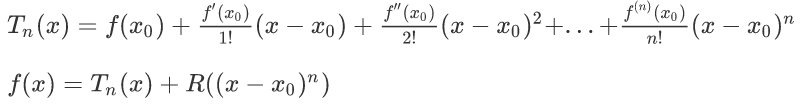前言

作为求解数论多项式题的必备知识，这几样东西每一样都不会讲得太深入，但是互相关联。

以下部分讲解摘自巨佬DY的"生成函数.pdf"。

~~（由于笔者对富文本编辑器情有独钟，下面的推导公式可能都是以无法复制的图片展示的）~~

微分求导

微分属于微积分的一部分，本来应该和积分一起讲，但是积分对微分依赖较大，而微分相对独立些，脱离微积分的情景也能讲懂。

求导和微分其实是一回事，微分的过程就是求导的过程。

把一个函数求导，通俗地讲，就是求出原函数每个点的切线斜率对应的函数，比如对于位移-时间图像，我们知道速度越大位移增长越快，某时刻切线斜率就等于该时刻的瞬时速度，所以位移-时间关系式求导过后就是速度-时间关系式。

我们称函数 $f(x)$ 求导过后的函数为 $f(x)$ 的导函数，记为 $(f(x))'$ 或 $f'(x)$ 。特别地，我们把函数 $f(x)$ 求导n次过后的函数叫做 $f(x)$ 的n阶导，可记为 $f^{(n)}(x)$ （注意不要写成 $f^n(x)$ ，这是 $f(x)$ 的n次方），所以 $f(x)$ 求导两次可以记为 $(f(x))''$ 、 $f''(x)$ ，也可以记为 $f^{(2)}(x)$ 。
有些函数可以求导，有些则不可导（如奇怪的折线）。

关于求导这里有一些很实用的需要背的东西（公式），建议熟记：

学习导数后你会发现一些有趣的东西，比如正余弦互化，比如 $e^x$ 导后不变，比如 $\frac{1}{1-x}$ 和 $\frac{x}{1-x}$ 的导函数相同，etc。

对微分求导更详细严谨的讲解可以看看《漫步微积分》（csdn上应该有人写了翻译博客）。

泰勒展开

泰勒展开，我的理解是，把一个非多项式的函数（比如指数对数，三角函数）写成一个多项式形式。

怎么让两者相等的？这里用到了导函数，标准公式为：

若 $f(x)$ 在n阶内可导：

$T_n(x)$ 称为 $f(x)$ 在点x0处(带有皮亚诺型余项)的泰勒多项式， $T_n(x)$ 的各项系数称为泰勒系数。

这里的x0是随便取的一个在定义域以内的值，R(x)是这个n次展开式的误差，叫做拉格朗日余项（一种皮亚诺型余项，了解即可，用得不多），如果x0和n取得得当，这个误差一般特别小。

n越大，展开式越精确，所以n=∞时可以把拉格朗日余项消去：

$f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2...=\sum_{i=0}^\infty \frac{f^{(i)}(x_0)}{i!}(x-x_0)^i$

（前提是 $f(x)$ 可以无限次求导）

特别地，当x0=0时，有麦克劳林公式：

$f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+R(x^n)$ 或 $f(x)=\sum_{i=0}^\infty \frac{f^{(i)}(0)}{i!}x^i$

至此，我们在多项式函数和非多项式函数之间建立了联系。

有一些常用的简单的例子，建议和导函数一起记：

$e^x=\sum_{i=0}^\infty \frac{x^i}{i!}$ ，这个很好解释， $e^x$ 求导后还是 $e^x$ ，带入麦克劳林公式即可。把x替换为-x还可以得到： $e^{-x}=\sum_{i=0}^\infty (-1)^i\frac{x^i}{i!}$ 。
$sin(x)=\sum_{i=0}^\infty (-1)^i\frac{x^{2i+1}}{(2i+1)!}$ ，因为 $(sin(x))'=cos(x),(cos(x))'=-sin(x)$ ，所以sin(x)的1阶、2阶、3阶、4阶导分别为 $cos(x)$ 、 $-sin(x)$ 、 $-cos(x)$ 、 $sin(x)$ ，然后循环，所以带入麦克劳林公式，偶数项泰勒系数都为0。
$cos(x)=\sum_{i=0}^\infty (-1)^i\frac{x^{2i}}{(2i)!}$ ，和sin(x)同理，cos(x)的1~4阶导为 $-sin(x)$ 、 $-cos(x)$ 、 $sin(x)$ 、 $cos(x)$ ，带入麦克劳林公式，系数和sin(x)的错位了一下，奇数项系数为0。
$\ln(x+1)=\sum_{i=1}^\infty(-1)^{i+1}\frac{x^i}{i}$ ，因为 $(\ln(x+1))'=\frac{1}{x+1}=(x+1)^{-1}$ ，然后再把右边的式子不断求导，可得 $\ln(x+1)$ 的n阶导为 $\frac{(-1)^{n+1}(n-1)!}{(x+1)^n}$ ，所以带入麦克劳林公式得到上式。为什么不写 $\ln(x)$ 呢？因为泰勒多项式自取的x0要满足在每一阶导的函数中都很好求， $\ln(x)$ 中就是1，但是如果x0取1的话多项式中会带 $(x-1)^i$ ，不方便看。如果把式子中的x替换为-x，就可以把所有系数都变为-1，得到： $\ln(1-x)=-\sum_{i=1}^\infty \frac{x^i}{i}, \sum_{i=1}^\infty\frac{x^i}{i}=-\ln(1-x)=\ln(\frac{1}{1-x})$
$\frac{1}{x+1}=\sum_{i=0}^\infty (-x)^i$ ，根据上面的过程可知 $\frac{1}{x+1}$ 的n阶导为 $\frac{(-1)^{n}(n)!}{(x+1)^{n+1}}$ ，带入麦克劳林公式后可以把阶乘消掉。
$(x+1)^a=\sum_{i=0}^\infty \frac{x^i}{i!}\prod_{j=0}^{i-1}(a-j)$ ，这个很显然； $\prod_{j=0}^{i-1}(a-j)$ 其实就是a的i次下降幂，当i>a时，显然这个式子为0，自动帮我们去除掉了求导a+1次过后导函数为0的情况。所以原式还可以长这样： $(x+1)^a=\sum_{i=0}^a \frac{x^i}{i!}\prod_{j=0}^{i-1}(a-j)$ 。

对泰勒展开更详细严谨的讲解可以看看别人的博客泰勒公式的展开细节解析（直接贴链接应该不存在什么版权问题吧，侵删）。

生成函数

生成函数也叫母函数，是很多组合排列题中用到的大法宝，只可惜我刚学，还完全不会用它解题。

普通生成函数

对于一个无穷序列 $\begin{Bmatrix}a_0,a_1,a_2,...\end{Bmatrix}$ ，定义其普通生成函数为形式幂级数： $\sum_{k=0}^\infty a_k\cdot x^k$ 。

为什么叫形式幂级数呢？它和普通幂级数有区别，加“形式”二字意思是它只是个形式上的关于x的多项式，在所有有关的推导中默认式子有意义，也就是不用管x的取值。

了解定义后，先看一些后面要用到的常用例子（建议熟记）：

序列 $\begin{Bmatrix}\frac{1}{0!},\frac{1}{1!},\frac{1}{2!},...,\frac{1}{k!},...\end{Bmatrix}$ 的普通生成函数： $e^x$ 。这 $\sum_{i=0}^\infty x^i$ 个很巧妙，因为根据定义得到的母函数为 $\sum_{i=0}^\infty \frac{x^i}{i!}$ ，正好是 $e^x$ 的泰勒展开。
序列 $\begin{Bmatrix}1,1,1,...,1,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-x}$ 。母函数为 $\sum_{i=0}^\infty x^i$ ，这就是一个无穷项的等比数列求和，当 $x\in (-1,1)$ 时，有求和公式 $\sum_{i=0}^\infty x^i=\frac{1}{1-x}$ ，因为母函数是形式幂级数，所以不管x的取值，直接等过去。
序列 $\begin{Bmatrix}1,2,4,...,2^k,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-2x}$ 。母函数为 $\sum_{i=0}^\infty 2^ix^i=\sum_{i=0}^\infty (2x)^i=\frac{1}{1-2x}$ 套等比数列求和公式。
序列 $\begin{Bmatrix}1,0,1,0,...,1,0,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-x^2}$ 。母函数为 $\sum_{i=0}^\infty x^{2i}=\sum_{i=0}^\infty (x^2)^i=\frac{1}{1-x^2}$ 。由此推广，两个1中间夹任意个数个0的序列的普通生成函数都可以用等比数列求和公式做。
序列 $\begin{Bmatrix}0,1,0,1,...,0,1,...\end{Bmatrix}$ 的普通生成函数： $\frac{x}{1-x^2}$ 。母函数为 $\sum_{i=0}^\infty x^{2i+1}=x\sum_{i=0}^\infty (x^2)^i=\frac{x}{1-x^2}$ 。
序列 $\begin{Bmatrix}1,2,3,...,k,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{(1-x)^2}$ 。这个也很巧妙，母函数为 $\sum_{i=0}^\infty (i+1)x^i$ ，发现正好是 $\sum_{i=0}^\infty x^{i+1}$ 的导函数，由于常数项求导会消去，所以也是 $\sum_{i=0}^\infty x^i$ 的导函数， $\sum_{i=0}^\infty x^i=\frac{1}{1-x}$ ，把 $\frac{1}{1-x}$ 求导后为 $\frac{1}{(1-x)^2}$ 。

应用

普通生成函数常用来解决无标号的组合计数问题。

例如在集合A中选i个数方案数为 $a_i$ ，集合B中选i个数方案数为 $b_i$ ，在A和B中共选i个数方案数为 $c_i$ ，显然满足 $c_i=\sum_{j=0}^ia^jb^{i-j}$ ，看起来正好是多项式乘法的卷积形式，因此序列 $\begin{Bmatrix}c_0,c_1,c_2,...,c_k,...\end{Bmatrix}$ 的普通生成函数 $F(c)$ 正好等于 $F(a)\cdot F(b)$ 。

有一道经典例题：

有四种无限多的水果，要求第一种恰好拿出偶数个，第二种恰好拿出 5 的倍数个，第三种最多拿 4 个，第四种最多拿 1 个，求恰好拿出 n 个水果的方案数。

显然可以直接看出答案，但是我们学以致用，用4个生成函数乘起来： $\frac{1}{1-x^2}\cdot \frac{1}{1-x^5}\cdot (\sum_{i=0}^4x^i)\cdot (1+x)=\frac{1}{1-x^2}\cdot \frac{1}{1-x^5}\cdot \frac{1-x^5}{1-x}\cdot (1+x)=\frac{1}{(1-x)^2}$ ，而 $\frac{1}{(1-x)^2}$ 正好是序列 $\begin{Bmatrix}1,2,3,...,k,...\end{Bmatrix}$ 的普通生成函数，所以答案为n+1。

求 Fibonacci 数列 $a_0 = a_1 = 1,a_n = a_{n-1} + a_{n-2}$ （n ≥ 2）的普通生成函数：

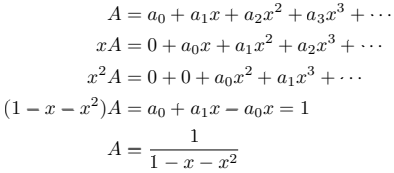
使用特征根法，即可得到 Fibonacci 数列的通项公式。

指数生成函数

对于一个无穷序列 $\begin{Bmatrix}a_0,a_1,a_2,...\end{Bmatrix}$ ，定义其指数生成函数为形式幂级数： $\sum_{k=0}^\infty a_k\cdot \frac{x^k}{k!}$ 。

应用

相较于普通生成函数，指数生成函数的实用性更高。普通生成函数通常用来解决无标号计数问题，指数生成函数通常用来解决带标号的计数问题，也就是排列计数。

同样举一个简单的例子，例如在集合A中选i个数的排列数为 $a_i$ ，集合B中选i个数的排列数为 $b_i$ ，在A和B中共选i个数的排列数为 $c_i$ ，显然满足 $c_i=\sum_{j=0}^i\binom{i}{j}a_jb_{i-j}=\sum_{j=0}^i\frac{i!}{j!(i-j)!}a_jb_{i-j}=\sum_{j=0}^ii!\frac{a_j}{j!}\frac{b_{i-j}}{(i-j)!}$ ， $\sum_{i=0}^\infty c_i\frac{x^i}{i!}=\sum_{i=0}^\infty x^i\sum_{j=0}^i\frac{a^j}{j!}\frac{b^{i-j}}{(i-j)!}=\sum_{i=0}^\infty \sum_{j=0}^ia_j\frac{x^j}{j!}\cdot b_{i-j}\frac{x^{i-j}}{(i-j)!}$ ，因此序列 $\begin{Bmatrix}c_0,c_1,c_2,...,c_k,...\end{Bmatrix}$ 的指数生成函数 $\hat{F}(c)$ 正好等于 $\hat{F}(a)\cdot \hat{F}(b)$ 。

一些例子：

n 个元素的排列数 $p_n=n!$ 的指数生成函数：。
n 个元素的环排列数 $c_n=(n-1)!$ （n ≥ 1）的指数生成函数： $\hat{C}(x)=\sum_{n=1}^\infty\frac{(n-1)!}{n!}x^n=\sum_{n=1}^\infty \frac{x^n}{n}=-\ln(1-x)=\ln(\frac{1}{1-x})$ ，你会发现 $\hat{P}(x)=e^{\hat{C}(x)}$ ，这不是巧合。你可以从排列置换的角度去理解（摘自永神OneInDark的博客）：
n 个元素的错排数（满足 $\forall i\in[1,n],p_i \neq i$ 的排列数）的指数生成函数：考虑错排数的容斥式，所以有 $\hat{D}(x)=\sum_{i=0}^\infty \frac{x^i}{i!}\sum_{j=0}^i\binom{i}{j}(-1)^j(i-j)! \\=\sum_{i=0}^\infty \sum_{j=0}^i\frac{(-1)^j}{j!}x^j\frac{(i-j)!}{(i-j)!}x^{i-j} \\=(\sum_{i=0}^\infty (-1)^i\frac{x^i}{i!})\cdot (\sum_{i=0}^\infty i!\frac{x^i}{i!})$ ，前面一坨等于 $e^{-x}$ 而后面一坨就是排列数的指数生成函数，所以 $\hat{D}(x)=\frac{e^{-x}}{1-x}$ 。

还有很多例子，我就不展开了，最重要的是做题积累经验。

干货

$e^x=\sum_{i=0}^\infty \frac{x^i}{i!}$ ， $e^{-x}=\sum_{i=0}^\infty (-1)^i\frac{x^i}{i!}$
$sin(x)=\sum_{i=0}^\infty (-1)^i\frac{x^{2i+1}}{(2i+1)!}$
$cos(x)=\sum_{i=0}^\infty (-1)^i\frac{x^{2i}}{(2i)!}$
$\ln(x+1)=\sum_{i=1}^\infty(-1)^{i+1}\frac{x^i}{i}$ ， $\ln(1-x)=-\sum_{i=1}^\infty \frac{x^i}{i}$ ， $\sum_{i=1}^\infty\frac{x^i}{i}=-\ln(1-x)=\ln(\frac{1}{1-x})$
$\frac{1}{x+1}=\sum_{i=0}^\infty (-x)^i$
$(x+1)^a=\sum_{i=0}^\infty \frac{x^i}{i!}\prod_{j=0}^{i-1}(a-j)=\sum_{i=0}^a \frac{x^i}{i!}\prod_{j=0}^{i-1}(a-j)$

序列 $\begin{Bmatrix}\frac{1}{0!},\frac{1}{1!},\frac{1}{2!},...,\frac{1}{k!},...\end{Bmatrix}$ 的普通生成函数： $e^x$
序列 $\begin{Bmatrix}1,1,1,...,1,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-x}$
序列 $\begin{Bmatrix}1,2,4,...,2^k,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-2x}$
序列 $\begin{Bmatrix}1,0,1,0,...,1,0,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{1-x^2}$
序列 $\begin{Bmatrix}0,1,0,1,...,0,1,...\end{Bmatrix}$ 的普通生成函数： $\frac{x}{1-x^2}$
序列 $\begin{Bmatrix}1,2,3,...,k,...\end{Bmatrix}$ 的普通生成函数： $\frac{1}{(1-x)^2}$
Fibonacci 数列 $a_0 = a_1 = 1,a_n = a_{n-1} + a_{n-2}$ （n ≥ 2）的普通生成函数： $\frac{1}{1-x-x^2}$

n 个元素的排列数的指数生成函数： $\hat{P}(x)=\frac{1}{1-x}$
n 个元素的环排列数的指数生成函数： $\hat{C}(x)=\ln(\frac{1}{1-x})$ ， $\hat{P}(x)=e^{\hat{C}(x)}$
n 个元素的错排数的指数生成函数： $\hat{D}(x)=\frac{e^{-x}}{1-x}$

浅谈微分求导+泰勒展开+生成函数

前言

微分求导

泰勒展开

生成函数

普通生成函数

应用

指数生成函数

应用

干货

猜你喜欢