引言
不熟悉马尔可夫模型以及里面的参数估计请务必先看文章马尔可夫模型。
我们以一个例子感受一下HMM是什么,隐这个字又代表什么。
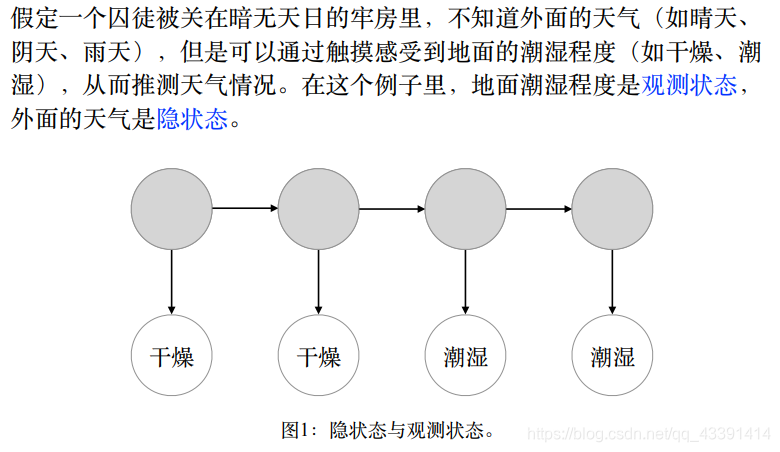
囚徒要根据观测状态(地面潮湿程度)推测外面的天气状况(隐状态)。如果你是聪明的囚徒,你可能会猜是:
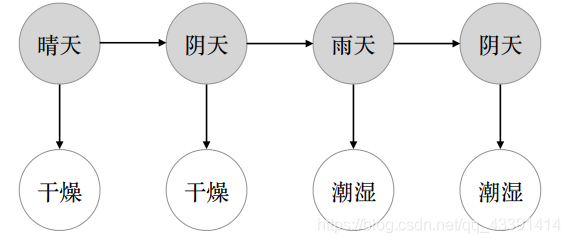
但是,囚徒是对的吗?或许(晴天,阴天,雨天,雨天)更好?口说无凭,我们用概率说话,哪个概率高,我们就选哪个。对这个问题,进行数学建模,这个模型就叫隐马尔可夫模型
三个问题
我们给出在这个数学模型可以回答的3个问题。换句话说,我们要建立隐马尔可夫模型来解决这3个问题。

这三个问题后面我们会依次提到,注意到,第二个问题就是囚徒要解决的问题,即估计外面的天气到底是什么?哪一个是最优的?
模型参数
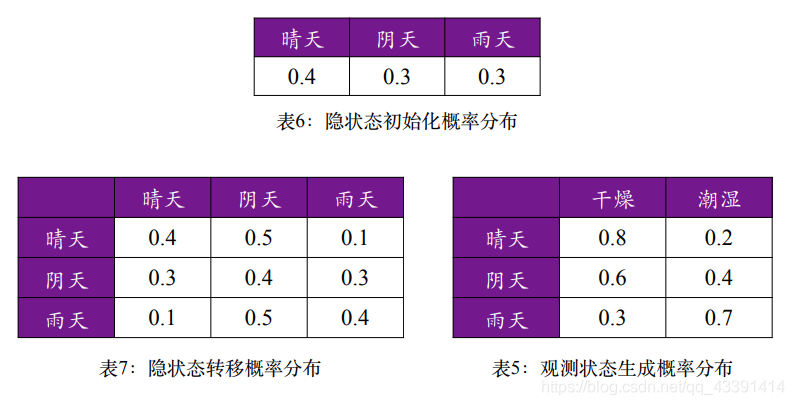
相比于马尔可夫模型中有的参数 π \pi π和 A A A,HMM多了一个 B B B,称为观测状态生成概率。
给个例子:
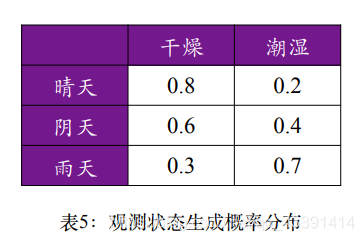
以上面第一行为例,如果外面天气是晴天(隐状态),那么牢房是干燥(观测状态)的概率是80%,是潮湿的概率是20%。
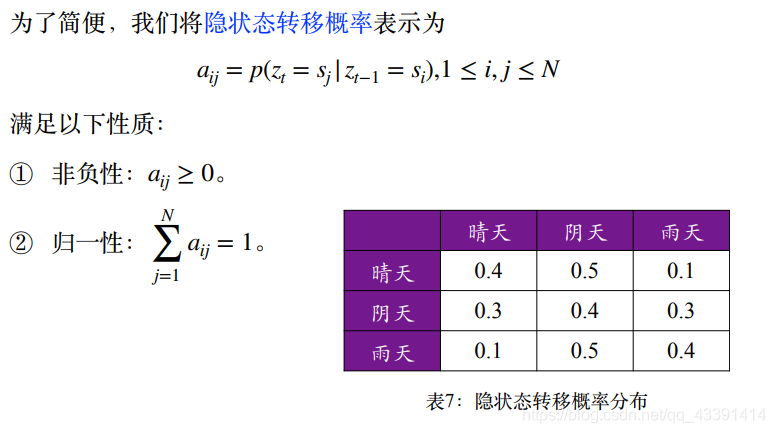
介绍完这个HMM中特有的 B B B,我们给出完整的三个参数的数学描述。

上面那个公式的解释:上面那个公式其实解决的是三个问题中的第一个问题,即计算观测状态序列 x = x 1 , x 2 , . . . . x T x=x_1,x_2,....x_T x=x1,x2,....xT的概率(拿囚徒的那个例子为例,我们要计算x=(干燥,干燥,潮湿,潮湿)发生的概率)。
- 第一行的公式使用的是全概率公式,穷举所有的 z z z, z z z是隐变量。
- 第二行的公式意思是:确定好隐变量 z z z之后,我们认为,观测状态是这样生成的:先生成第一个隐状态,概率为 p ( z 1 ) p(z_1) p(z1),有了这个隐状态之后,生成观测状态 x 1 x_1 x1,概率为 p ( x 1 ∣ z 1 ) p(x_1|z_1) p(x1∣z1),然后隐状态还要生成下一个隐状态 z 2 z_2 z2,概率为 p ( z 2 ∣ z 1 ) p(z_2|z_1) p(z2∣z1),然后有了第2个隐状态之后,又生成第2个观测状态,概率为 p ( x 2 ∣ z 2 ) p(x_2|z_2) p(x2∣z2)。依次类推,就可以得到我们的第二行的公式,此时将观测状态 x = x 1 , x 2 , . . . . x T x=x_1,x_2,....x_T x=x1,x2,....xT全部生成完毕。
上面 θ \theta θ的解释: θ = ( π , A , B ) \theta=(\pi ,A,B) θ=(π,A,B)
三个参数
π \pi π

A A A
B B B

解决第一个问题
第一个问题在前面就已经解出来了,即使用全概率公式穷举所有隐变量 z z z:
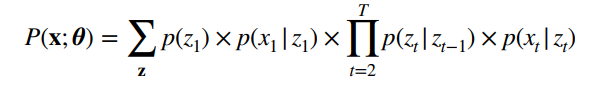
但是,这样解效率太低。举个例子,我们要计算观测状态序列x=(干燥,潮湿)的概率。那么我们要穷举所有的隐状态序列:

然后9个都可以得到一个概率,然后相加,就是 p ( x ; θ ) p(x;\theta ) p(x;θ)。
显然:

有没有什么更快的方法呢?借助图来看看。
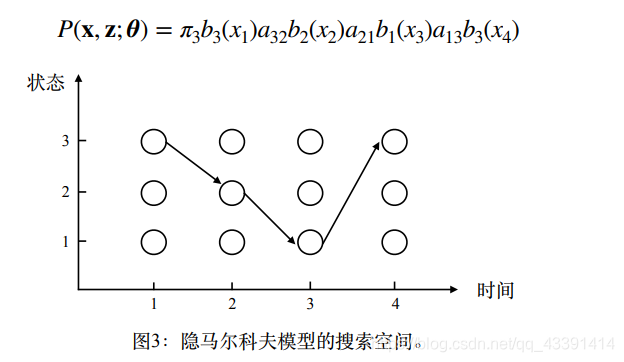
我们为了和图对应,重新假设观测状态序列长度为4,隐状态个数为3。那么一个从开始到结束的单向箭头就表示一个我们枚举的一个隐状态序列,比如上面是(3,2,1,3)。
但是由公式
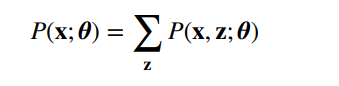
所以我们要对所有的单向箭头穷举,然后分别计算,最后加起来。
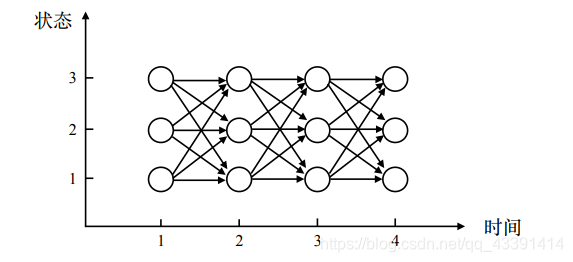
例子
我们举个实际的例子,来体会一下,不过,你先记住要穷举,分别计算,然后相加。
假设由下面的图,那么最后的结果是什么?
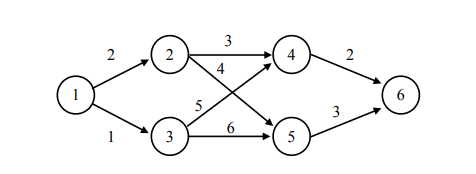

最后的结果是64,学过数据结构的人肯定要疑问,一条路的路径长度不应该是路径上边的权值相加吗,这里怎么是相乘?其实这都没有关系。我们这里是为了和HMM一样,前几幅图中有个公式已经说清楚了。
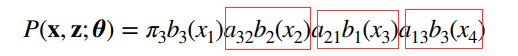
前面已经说过了,对于一条路径 z z z,计算的时候是乘法如上。
动态规划算法
上面这样穷举似乎太低效了,所以我们期望更好的方法,因此考虑使用动态规划算法,我们知道动态规划算法需要2个核心步骤,一个是将原问题分解成子问题,然后确定转移方程。我们先把这个解决。

大家可以好好理解一下,上面这个公式对不对,理解透了往下走。
接下来,我们解决动态规划的另外一个核心步骤,写出初始状态。
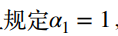
同时也好好理解下,这个为什么要这样设置。如果没明白,我们先用上面两个式子用一遍,再回过头来就明白为什么这样了。
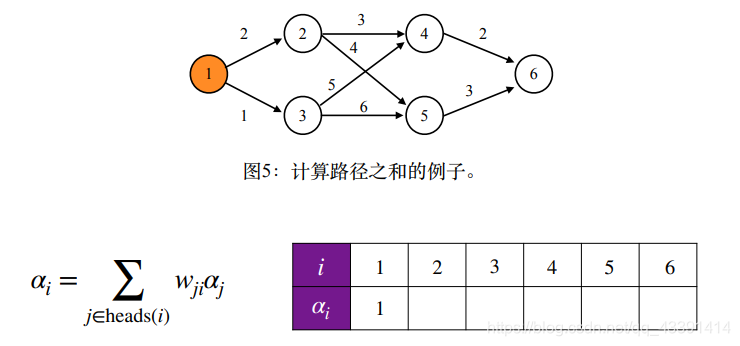
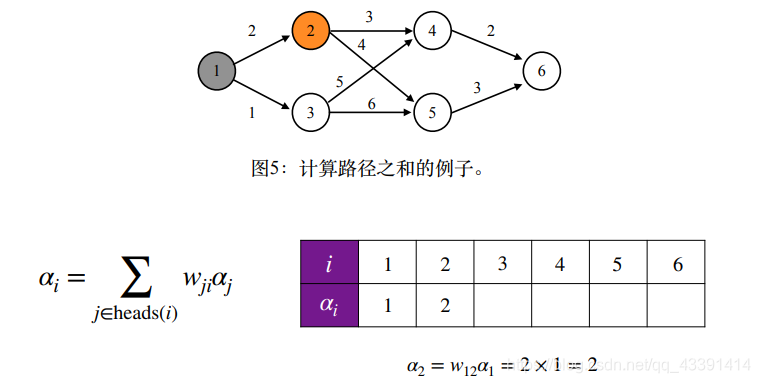
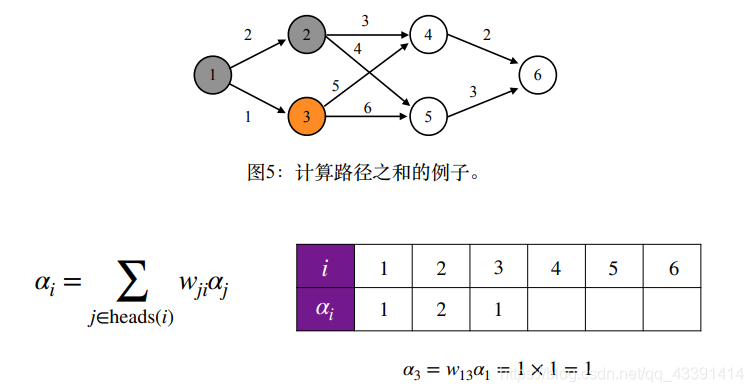
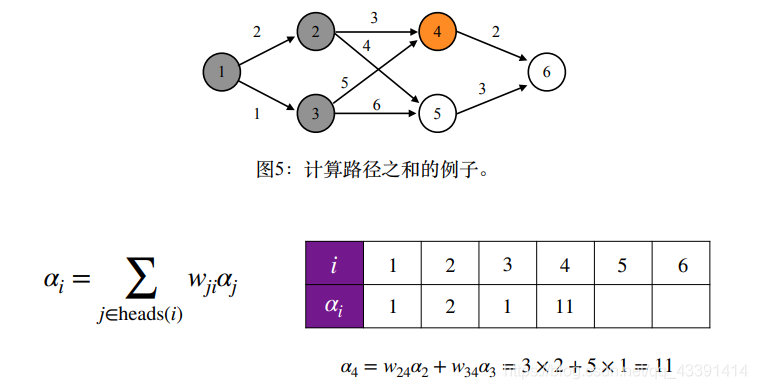
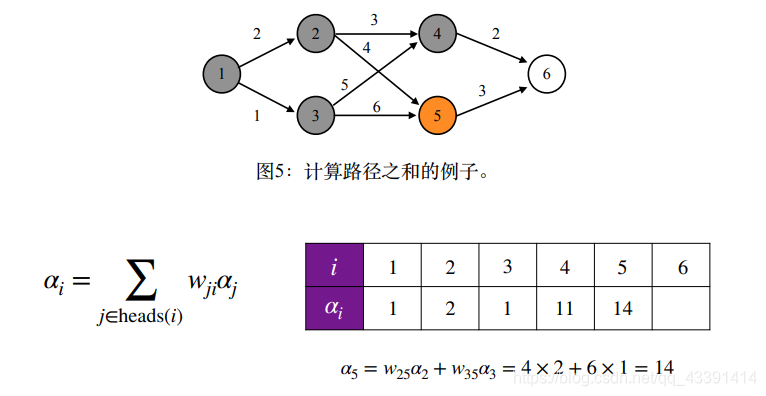

结果是64,和我们全枚举4条路经加起来的结果是一样的。
前向概率
这是一个非常重要的概念,务必理解。
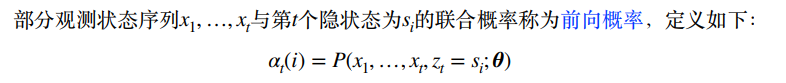
你需要理解到的是:
前向概率和 p ( x ; θ ) p(x;\theta ) p(x;θ)关系密切,使用全概率公式有:
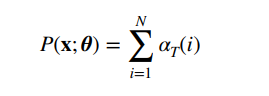
但是我们不知道
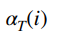
这个是T时刻的,正好用上面学的动态规划算法计算,即先算1时刻的:
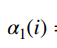
然后从1时刻往后推。
下面给出这个递推过程,图D。

上面的初始化根据前向概率的定义是很容易理解的。然后再理解一下第二递推公式,这个也是根据前向概率的定义来的。你可以展开左边的,然后用条件概率推一推就得到了。
α t ( j ) = p ( x 1 , x 2 , . . . , x t − 1 , z t = s j , x t ) = p ( x t ∣ x 1 , x 2 , . . . , x t − 1 , z t = s j ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t = s j ) = p ( x t ∣ z t = s j ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t = s j ) = b j ( x t ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t = s j ) \alpha_t(j)=p(x_1,x_2,...,x_{t-1},z_t=s_j,x_t)=p(x_t|x_1,x_2,...,x_{t-1},z_t=s_j)*p(x_1,x_2,...,x_{t-1},z_t=s_j)=p(x_t|z_t=s_j)*p(x_1,x_2,...,x_{t-1},z_t=s_j)=b_j(x_t)*p(x_1,x_2,...,x_{t-1},z_t=s_j) αt(j)=p(x1,x2,...,xt−1,zt=sj,xt)=p(xt∣x1,x2,...,xt−1,zt=sj)∗p(x1,x2,...,xt−1,zt=sj)=p(xt∣zt=sj)∗p(x1,x2,...,xt−1,zt=sj)=bj(xt)∗p(x1,x2,...,xt−1,zt=sj)
解释:上面那一步缩减的那里是因为 x t x_t xt发生的概率不依赖于 x 1 , x 2 , . . . , x t − 1 x_1,x_2,...,x_{t-1} x1,x2,...,xt−1。然后我们对乘号后面的继续做处理。
进行全概率公式展开,有:
p ( x 1 , x 2 , . . . , x t − 1 , z t = s j ) = ∑ i = 1 N p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i , z t = s j ) = ∑ i = 1 N p ( z t = s j ∣ x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) = p ( z t = s j ∣ z t − 1 = s i ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) = ∑ i = 1 N a i j ∗ α t − 1 ( i ) p(x_1,x_2,...,x_{t-1},z_t=s_j)=\sum_{i=1}^Np(x_1,x_2,...,x_{t-1},z_{t-1}=s_i,z_t=s_j)=\sum_{i=1}^Np(z_t=s_j|x_1,x_2,...,x_{t-1},z_{t-1}=s_i)*p(x_1,x_2,...,x_{t-1},z_{t-1}=s_i)=p(z_t=s_j|z_{t-1}=s_i)*p(x_1,x_2,...,x_{t-1},z_{t-1}=s_i)=\sum_{i=1}^Na_{ij}*\alpha_{t-1}(i) p(x1,x2,...,xt−1,zt=sj)=∑i=1Np(x1,x2,...,xt−1,zt−1=si,zt=sj)=∑i=1Np(zt=sj∣x1,x2,...,xt−1,zt−1=si)∗p(x1,x2,...,xt−1,zt−1=si)=p(zt=sj∣zt−1=si)∗p(x1,x2,...,xt−1,zt−1=si)=∑i=1Naij∗αt−1(i)
最后结合起来就是:
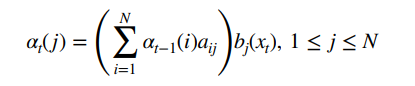
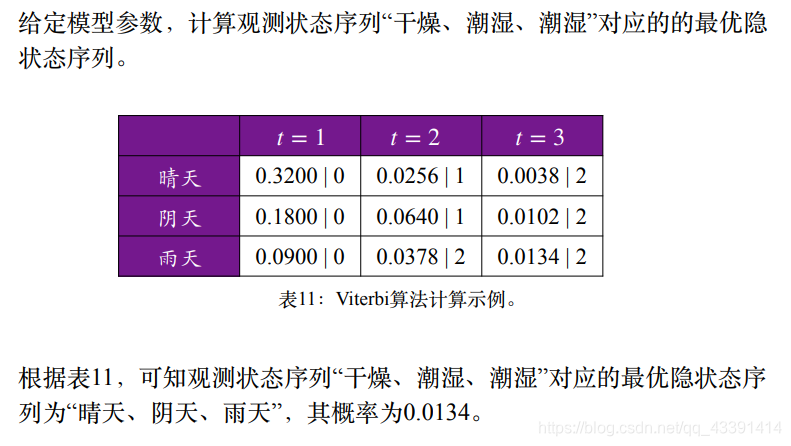
下面给个例子,正好回答第三个问题中的第一个问题。

给定参数。
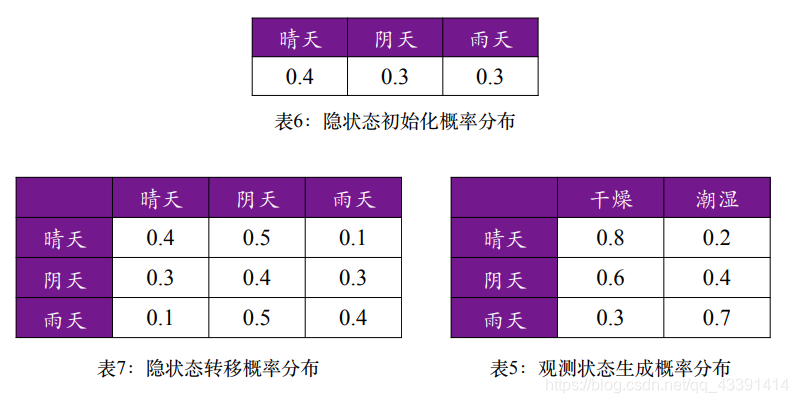
我们利用前向概率,并用图D可以算得:
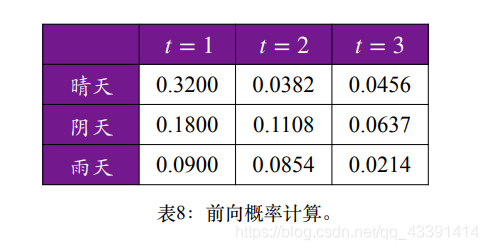
举个例子,根据图D的第一个公式,上面第一行第一列为前向概率 α 1 ( 晴 天 ) \alpha_1(晴天) α1(晴天),也即 P ( x 1 = 干 燥 , z t = 晴 天 ) = 0.4 ∗ 0.8 = 0.32 P(x_1=干燥,z_t=晴天)=0.4*0.8=0.32 P(x1=干燥,zt=晴天)=0.4∗0.8=0.32,然后继续用第一个公式算第二行第一列,第三行第一列。
根据之前的图D的第二个公式,可以依次算到第二列,第三列 α 2 ( i ) , α 3 ( i ) \alpha_2(i),\alpha_3(i) α2(i),α3(i)。
最后,利用图D的第三个公式得到观测状态序列概率。

后向概率
又来了一个非常重要的概念,需要好好理解。图DD。

上面的初始化根据后向概率的定义是合理的。然后再理解一下第二递推公式,这个也是根据后向概率的定义来的。你可以展开左边的,然后用条件概率推一推就得到了。
β t ( i ) = p ( x t + 1 , x t + 2 , , , , x T ∣ z t = s i ) = ∑ j = 1 N p ( x t + 1 , x t + 2 , , , , x T , z t + 1 = s j ∣ z t = s i ) = ∑ j = 1 N p ( x t + 1 , x t + 2 , , , , x T ∣ z t = s i , z t + 1 = s j ) ∗ p ( z t + 1 = s j ∣ z t = s i ) = ∑ j = 1 N p ( x t + 1 , x t + 2 , , , , x T ∣ z t = s i , z t + 1 = s j ) ∗ a i j = ∑ j = 1 N p ( x t + 2 , , , , x T ∣ x t + 1 , z t = s i , z t + 1 = s j ) ∗ p ( x t + 1 ∣ z t = s i , z t + 1 = s j ) ∗ a i j = ∑ j = 1 N p ( x t + 2 , , , , x T ∣ x t + 1 , z t = s i , z t + 1 = s j ) ∗ b j ( x t + 1 ) ∗ a i j = ∑ j = 1 N p ( x t + 2 , , , , x T ∣ z t + 1 = s j ) ∗ b j ( x t + 1 ) ∗ a i j = ∑ j = 1 N β t + 1 ( j ) ∗ b j ( x t + 1 ) ∗ a i j \beta_t(i)=p(x_{t+1},x_{t+2},,,,x_T|z_t=s_i)=\sum_{j=1}^Np(x_{t+1},x_{t+2},,,,x_T,z_{t+1}=s_j|z_t=s_i)=\sum_{j=1}^Np(x_{t+1},x_{t+2},,,,x_T|z_t=s_i,z_{t+1}=s_j)*p(z_{t+1}=s_j|z_t=s_i)=\sum_{j=1}^Np(x_{t+1},x_{t+2},,,,x_T|z_t=s_i,z_{t+1}=s_j)*a_{ij}=\sum_{j=1}^Np(x_{t+2},,,,x_T|x_{t+1},z_t=s_i,z_{t+1}=s_j)*p(x_{t+1}|z_t=s_i,z_{t+1}=s_j)*a_{ij}=\sum_{j=1}^Np(x_{t+2},,,,x_T|x_{t+1},z_t=s_i,z_{t+1}=s_j)*b_j(x_{t+1})*a_{ij}=\sum_{j=1}^Np(x_{t+2},,,,x_T|z_{t+1}=s_j)*b_j(x_{t+1})*a_{ij}=\sum_{j=1}^N\beta_{t+1}(j)*b_j(x_{t+1})*a_{ij} βt(i)=p(xt+1,xt+2,,,,xT∣zt=si)=∑j=1Np(xt+1,xt+2,,,,xT,zt+1=sj∣zt=si)=∑j=1Np(xt+1,xt+2,,,,xT∣zt=si,zt+1=sj)∗p(zt+1=sj∣zt=si)=∑j=1Np(xt+1,xt+2,,,,xT∣zt=si,zt+1=sj)∗aij=∑j=1Np(xt+2,,,,xT∣xt+1,zt=si,zt+1=sj)∗p(xt+1∣zt=si,zt+1=sj)∗aij=∑j=1Np(xt+2,,,,xT∣xt+1,zt=si,zt+1=sj)∗bj(xt+1)∗aij=∑j=1Np(xt+2,,,,xT∣zt+1=sj)∗bj(xt+1)∗aij=∑j=1Nβt+1(j)∗bj(xt+1)∗aij
解释:上面所有缩减 p ( x ∣ y , z ) = p ( x ∣ y ) p(x|y,z)=p(x|y) p(x∣y,z)=p(x∣y),是因为x和z没有关系。
还是上面那个计算的例子,我们也可以通过后向概率计算得到观测状态序列的概率。
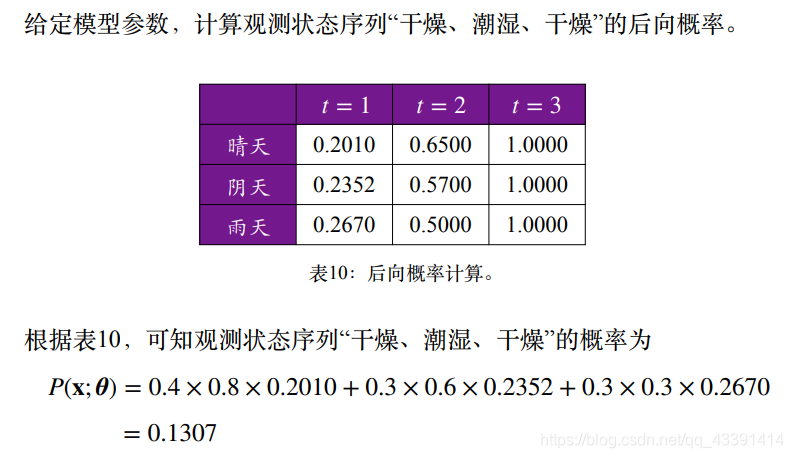
和前向概率的计算是吻合的。
干掉第二个问题
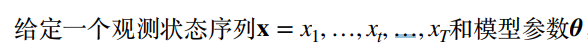
如何计算最优隐状态?
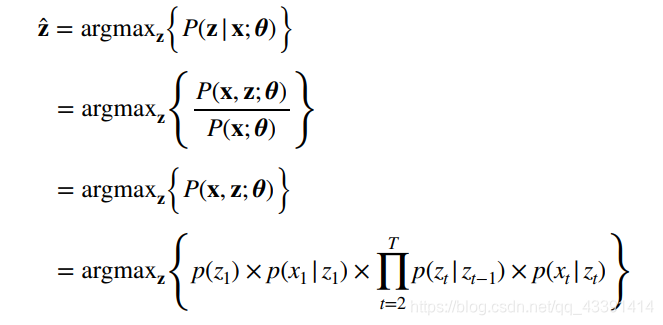
从图的角度看,第一个问题是是所有的路相加,现在第二个问题是选一条最大的路。
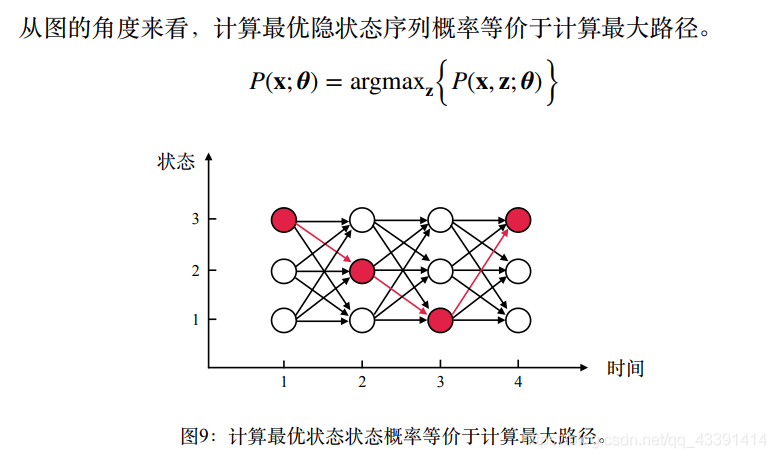
还是拿以前的例子:
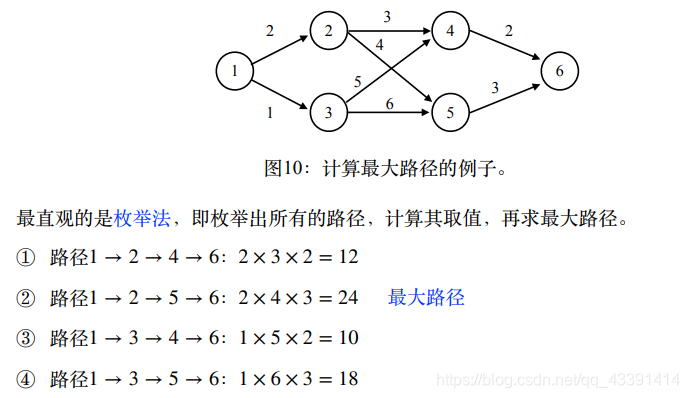
我们还是想要寻求更快的算法,而不是枚举法。
同样,我们使用动态规划算法。
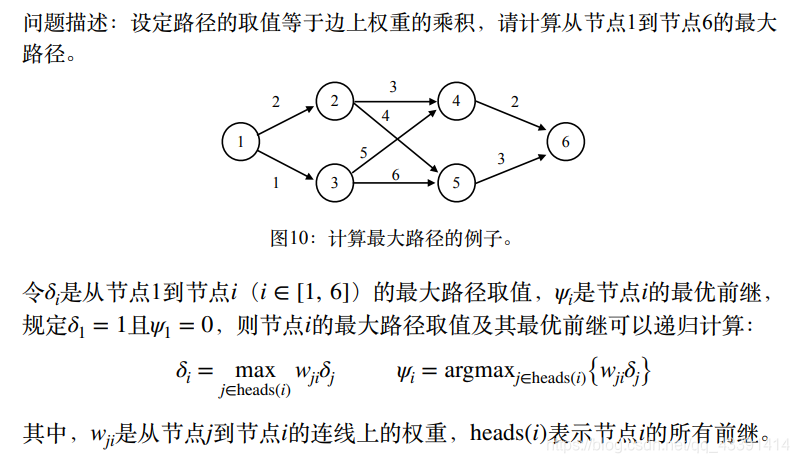
第二个公式是,记录最优路径序列,否则只算个路径长度没有用啊,我们要记住最优隐状态序列。这个数据结构中的最短路径算法一样,不但要算最短路径是多少,还要得到这条路经过了哪些节点,是怎么走的,所以里面有一个path数组。
例子。
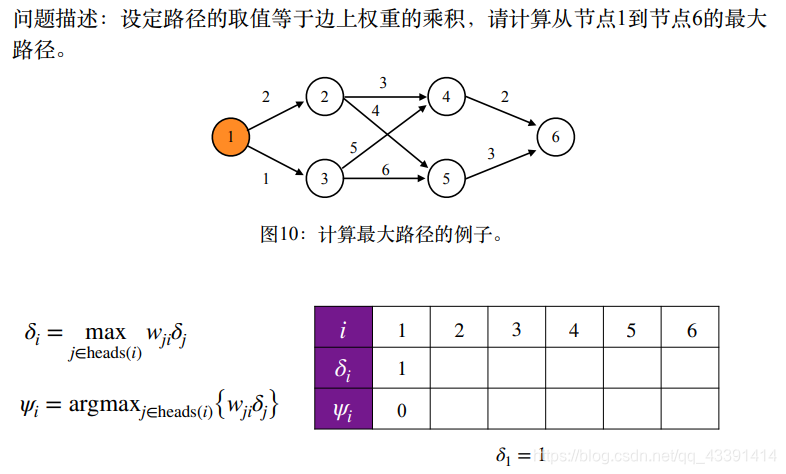
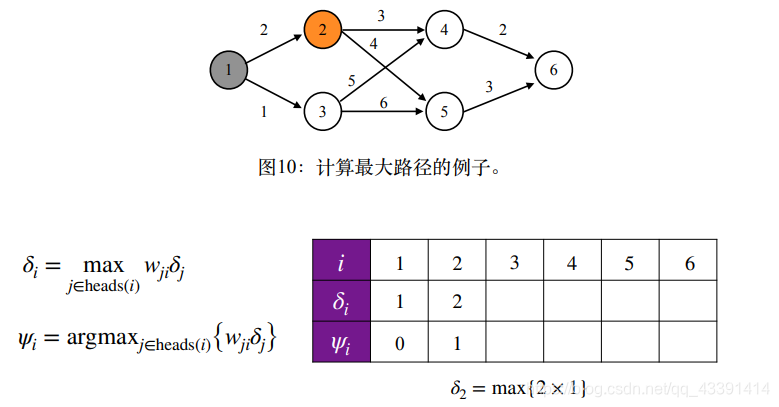
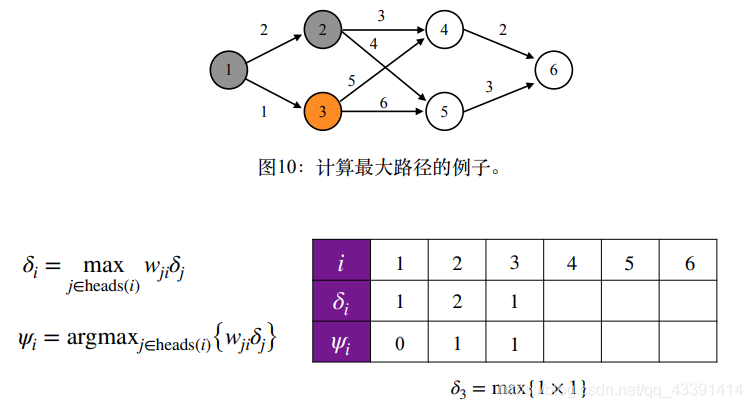
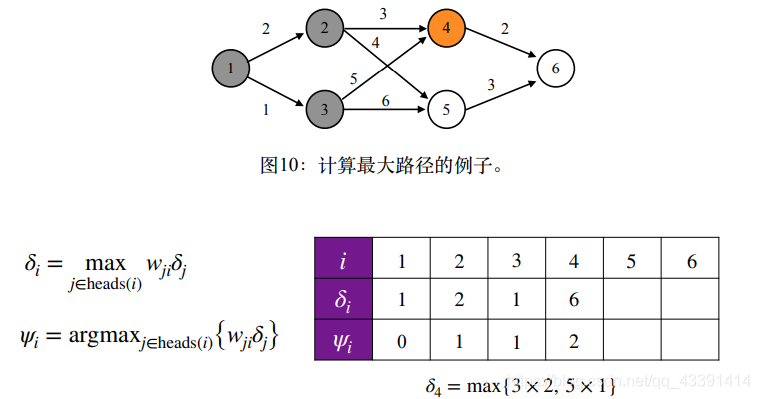
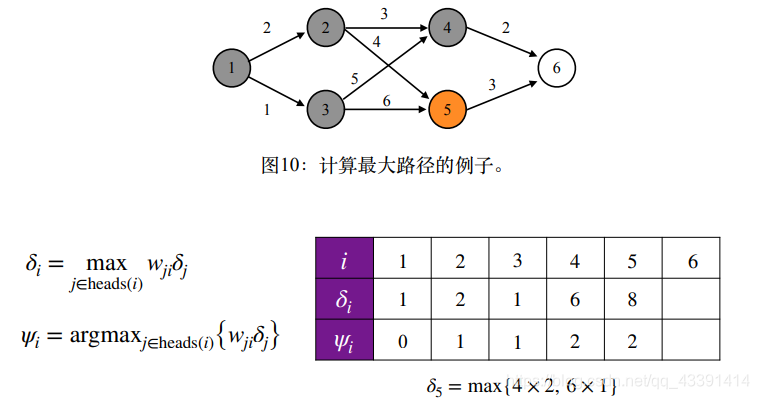
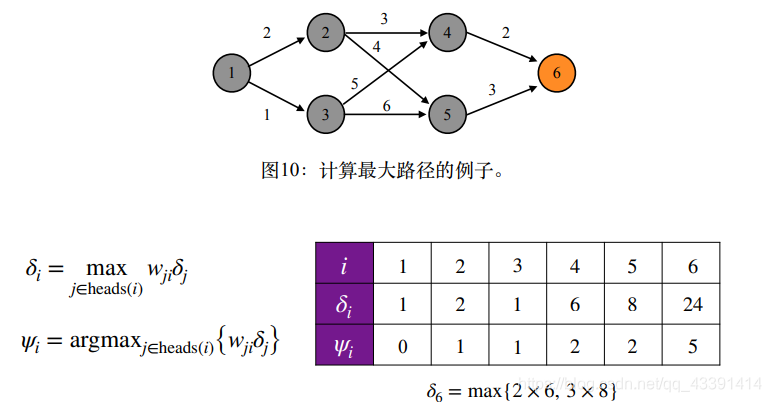
巧妙之处在于,在表格的第2行中,我们记录了最优路径序列。
回溯找到最长路径。
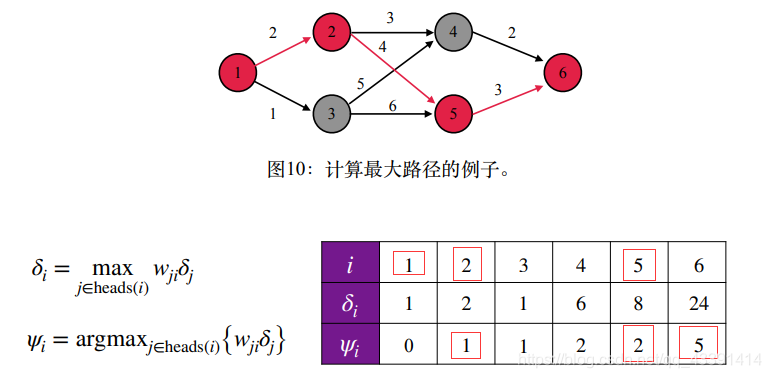
Viterbi算法
有了上面这个例子的经验,我们回到我们的问题有viterbi算法,解决了最优隐状态的计算。

有了前面的例子,这个很好理解,不做解释。
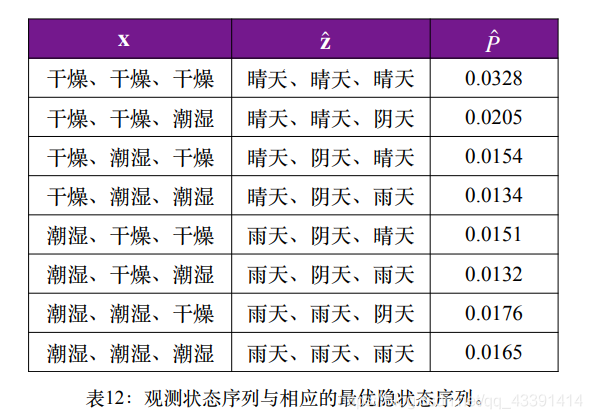
让大家放松一下,看看下图,看看最优隐状态符不符合你的直觉。
攻克第三个问题
第三个问题是:


不知道马尔可夫模型的参数估计的看文章马尔可夫模型。
对上图的解释:
为什么要用全概率展开,因为如果没有隐状态序列z, p ( x ( d ) ; θ ) p(x^{(d)};\theta) p(x(d);θ)表达式都写不出来。 只有穷举出z来,才有表达式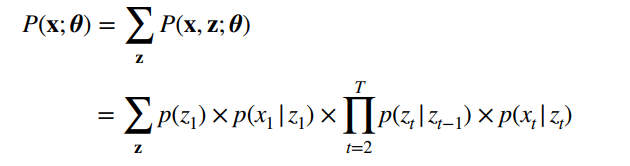
穷举了之后到了最后一部,直接求导为0,参数 θ \theta θ不是出来了吗?,这个log里面还有求和,求导会很复杂,一般都求不出来(如果可以有解析解,欢迎告诉我,我也不知道有没有)。
EM算法
我们仍然想和以前一样,写出拉格朗日函数求参数 θ = ( π , A , B ) \theta =(\pi,A,B) θ=(π,A,B)。忘了的,可以看我文章开头那篇文章。

然后得到下面计数的函数。

要是像上面那样就好了,可惜不是。
大家应该注意到了,上上幅图有一个唯一的不同之处,就是有个前缀。
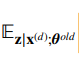
这麻烦了,这表示什么意思呢?我们由于不知道观测数据的隐状态是什么,按照前面说的,那么就写不出表达式 p ( x ( d ) ; θ ) p(x^{(d)};\theta) p(x(d);θ)。现在我们这样做,先随便假设一个 θ 0 = ( π 0 , A 0 , B 0 ) \theta_0 =(\pi_0,A_0,B_0) θ0=(π0,A0,B0),然后根据我们三个问题中的第二个问题,我们可以为每一个观测序列估计隐状态。现在有两种做法:
- 为每一个观测序列利用 θ 0 \theta_0 θ0分配一个最优隐状态,那么根据上幅图的计数函数,直接算出了参数,并作为新的参数 θ 1 \theta_1 θ1。
- 不指明是哪一个状态,而是以一定的概率分配到所有隐状态上,即这个观测序列所真实对应地隐状态未必是你算的最优隐状态,因为你算的那个只是概率比较大而已,如果真实不是你算的那个,那损失岂不是很大,被你错判了。所以以概率形式分配隐状态,不丢失任何信息,这也正是纯生成式模型的特点,所有都以概率说话。
我们以第2种方式处理,那么我们就要算期望,它表示平均意义下隐状态是什么。
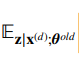
那么既然如此,上面的参数估计的那个计数也要变成期望了,即平均上是多少。
以第2个为例,其形式为:
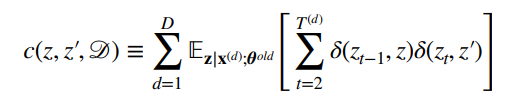
就是多了那么个符号而已,可以把那个期望提到外面去,总之表示平均来说计数是多少。
我们把期望的那个符号,放到最里面去,然后继续做下去:
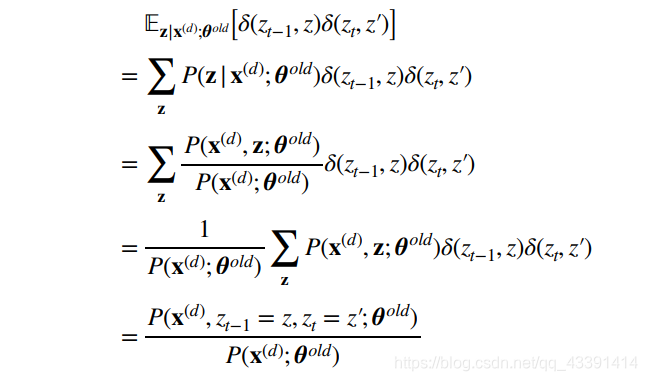
解释:有了前面说的不指派一个z,而是给所有z一定的概率,那么期望变成概率求和应该很好理解了。
倒数第2步变成倒数第一步非常精彩,理解后面两个对比函数乘积的概念就很明显了,不明白意思的可以看下开头的文章。这里再做一点解释,后面两个对比函数乘积为1,表示 z t − 1 = z , z t = z ′ z_{t-1}=z,z_t=z^{'} zt−1=z,zt=z′,否则为0。所以这个函数的目的是让所有的隐状态有这个特征的都留下来,那就是倒数第一步的分子喽。
打个比方,假设枚举了3个隐状态序列,假设这3个隐状态序列的概率都是1/3。假设现在要匹配特征 z 2 = 晴 天 , z 3 = 雨 天 z_{2}=晴天,z_3=雨天 z2=晴天,z3=雨天
(阴天,晴天,雨天)
(晴天,晴天,雨天)
(雨天,雨天,雨天)
那么倒数第二步的分子相当于
1/3*1*1+1/3*1*1+1/3*0*1=2/3
另一方面,对所有隐状态来说, p ( z 2 = 晴 天 , z 3 = 雨 天 ) p(z_{2}=晴天,z_3=雨天) p(z2=晴天,z3=雨天)不也是2/3吗?
倒数第2步变成倒数第一步,现在应该理解了。
现在别忘了目的,我们要计算
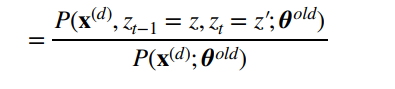
上面的分母就是我们三个问题中的第一个问题


首先要提醒的是,我们把 z t − 1 = z , z t = z ′ z_{t-1}=z,z_t=z^{'} zt−1=z,zt=z′换成我们熟悉的形式 z t − 1 = s i , z t = s j z_{t-1}=s_i,z_t=s_j zt−1=si,zt=sj,注意到这不会没有影响什么。因为对于一个隐状态z,你总是能找到它的下标。
比如状态集合 S = 晴 天 , 雨 天 , 阴 天 S={晴天,雨天,阴天} S=晴天,雨天,阴天,那么 z t − 1 = 晴 天 , z t = 阴 天 z_{t-1}=晴天,z_t=阴天 zt−1=晴天,zt=阴天可以替换成 z t − 1 = S 1 , z t = S 3 z_{t-1}=S_1,z_t=S_3 zt−1=S1,zt=S3,这都是一一对应的。
公式的推导
这个和前向后向概率是一样的推导,条件概率展开即可。
p ( x 1 , . . . . . . , x t − 1 , x t , x t + 1 , . . . x T , z t − 1 = s i , z t = s j ) = p ( x 1 , . . . . . . , x t − 1 , z t − 1 = s i ) ∗ p ( x t , x t + 1 , . . . x T , z t = s j ∣ x 1 , . . . . . . , x t − 1 , z t − 1 = s i ) = α t − 1 ( i ) ∗ p ( x t , x t + 1 , . . . x T , z t = s j ∣ x 1 , . . . . . . , x t − 1 , z t − 1 = s i ) = α t − 1 ( i ) ∗ p ( x t , x t + 1 , . . . x T , z t = s j ∣ z t − 1 = s i ) = α t − 1 ( i ) ∗ p ( x t , x t + 1 , . . . x T ∣ z t = s j , z t − 1 = s i ) ∗ p ( z t = s j ∣ z t − 1 = s i ) = α t − 1 ( i ) ∗ p ( x t , x t + 1 , . . . x T ∣ z t = s j , z t − 1 = s i ) ∗ a i j = α t − 1 ( i ) ∗ p ( x t + 1 , . . . x T ∣ x t , z t = s j , z t − 1 = s i ) ∗ p ( x t ∣ z t = s j , z t − 1 = s i ) ∗ a i j = α t − 1 ( i ) ∗ p ( x t + 1 , . . . x T ∣ x t , z t = s j , z t − 1 = s i ) ∗ b j ( x t ) ∗ a i j = α t − 1 ( i ) ∗ p ( x t + 1 , . . . x T ∣ z t = s j , z t − 1 = s i ) ∗ b j ( x t ) ∗ a i j = α t − 1 ( i ) ∗ p ( x t + 1 , . . . x T ∣ z t = s j ) ∗ b j ( x t ) ∗ a i j = α t − 1 ( i ) ∗ β t ( j ) ∗ b j ( x t ) ∗ a i j p(x1,......,x_{t-1},x_t,x_{t+1},...x_T,z_{t-1}=s_i,z_t=s_j)=p(x1,......,x_{t-1},z_{t-1}=s_i)*p(x_t,x_{t+1},...x_T,z_t=s_j|x1,......,x_{t-1},z_{t-1}=s_i)=\alpha_{t-1}(i)*p(x_t,x_{t+1},...x_T,z_t=s_j|x1,......,x_{t-1},z_{t-1}=s_i)=\alpha_{t-1}(i)*p(x_t,x_{t+1},...x_T,z_t=s_j|z_{t-1}=s_i)=\alpha_{t-1}(i)*p(x_t,x_{t+1},...x_T|z_t=s_j,z_{t-1}=s_i)*p(z_t=s_j|z_{t-1}=s_i)=\alpha_{t-1}(i)*p(x_t,x_{t+1},...x_T|z_t=s_j,z_{t-1}=s_i)*a_{ij}=\alpha_{t-1}(i)*p(x_{t+1},...x_T|x_t,z_t=s_j,z_{t-1}=s_i)*p(x_t|z_t=s_j,z_{t-1}=s_i)*a_{ij}=\alpha_{t-1}(i)*p(x_{t+1},...x_T|x_t,z_t=s_j,z_{t-1}=s_i)*b_j(x_t)*a_{ij}=\alpha_{t-1}(i)*p(x_{t+1},...x_T|z_t=s_j,z_{t-1}=s_i)*b_j(x_t)*a_{ij}=\alpha_{t-1}(i)*p(x_{t+1},...x_T|z_t=s_j)*b_j(x_t)*a_{ij}=\alpha_{t-1}(i)*\beta_t(j)*b_j(x_t)*a_{ij} p(x1,......,xt−1,xt,xt+1,...xT,zt−1=si,zt=sj)=p(x1,......,xt−1,zt−1=si)∗p(xt,xt+1,...xT,zt=sj∣x1,......,xt−1,zt−1=si)=αt−1(i)∗p(xt,xt+1,...xT,zt=sj∣x1,......,xt−1,zt−1=si)=αt−1(i)∗p(xt,xt+1,...xT,zt=sj∣zt−1=si)=αt−1(i)∗p(xt,xt+1,...xT∣zt=sj,zt−1=si)∗p(zt=sj∣zt−1=si)=αt−1(i)∗p(xt,xt+1,...xT∣zt=sj,zt−1=si)∗aij=αt−1(i)∗p(xt+1,...xT∣xt,zt=sj,zt−1=si)∗p(xt∣zt=sj,zt−1=si)∗aij=αt−1(i)∗p(xt+1,...xT∣xt,zt=sj,zt−1=si)∗bj(xt)∗aij=αt−1(i)∗p(xt+1,...xT∣zt=sj,zt−1=si)∗bj(xt)∗aij=αt−1(i)∗p(xt+1,...xT∣zt=sj)∗bj(xt)∗aij=αt−1(i)∗βt(j)∗bj(xt)∗aij
上面非常详细,没有之一。
然后,我们将上面这个带回到
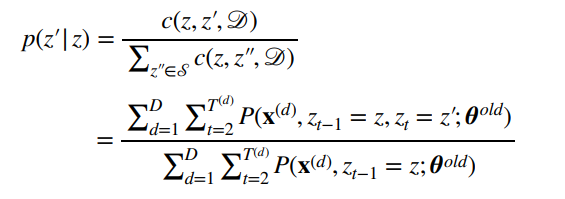
带入结果。
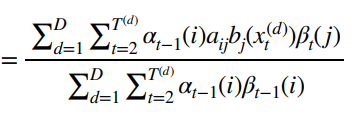
有人发现,分母不一样,即上面是

而下面是
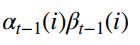
这两个是相等的,证明也是类似的:
p ( x 1 , x 2 , . . . . . , x t − 1 , x t , . . . x T , z t − 1 = s i ) = p ( x t , . . . . x T ∣ x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) = p ( x t , . . . . x T ∣ z t − 1 = s i ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) = β t − 1 ( i ) ∗ p ( x 1 , x 2 , . . . , x t − 1 , z t − 1 = s i ) ∗ β t − 1 ( i ) ∗ α t − 1 ( i ) p(x_1,x_2,.....,x_{t-1},x_t,...x_T,z_{t-1}=s_i)=p(x_t,....x_T|x_1,x_2,...,x_{t-1},z_{t-1}=s_i)*p(x1,x2,...,x_{t-1},z_{t-1}=s_i)=p(x_t,....x_T|z_{t-1}=s_i)*p(x1,x2,...,x_{t-1},z_{t-1}=s_i)=\beta_{t-1}(i)*p(x1,x2,...,x_{t-1},z_{t-1}=s_i)*\beta_{t-1}(i)*\alpha_{t-1}(i) p(x1,x2,.....,xt−1,xt,...xT,zt−1=si)=p(xt,....xT∣x1,x2,...,xt−1,zt−1=si)∗p(x1,x2,...,xt−1,zt−1=si)=p(xt,....xT∣zt−1=si)∗p(x1,x2,...,xt−1,zt−1=si)=βt−1(i)∗p(x1,x2,...,xt−1,zt−1=si)∗βt−1(i)∗αt−1(i)
总结
本文写得比较长,较为详细的介绍了HMM的三个问题以及相应的解决办法,其中为了解决指数空间的求和问题,我们反复使用了动态规划算法,为了解决第二个问题,用了viterbi算法,解决第3个问题用了baum-welch算法,EM算法。
这其中,用到的数学公式其实真的不多,大家掌握好条件概率,全概率,拉格朗日乘子法求极值,求期望就够了,其他都只剩下理解了公式所代表的物理含义罢了。
写在结尾:本文写得比较长,也花费了比较多的时间,请大家尊重我的劳动,未得到我的许可,请不要转载。另外,本文有什么需要补充的地方,欢迎在评论区留言,一起完善。