1. 马尔可夫模型
下面介绍几个马尔可夫模型中的重要概念:
1.1 一阶马尔可夫假设 (first order Markov assumption)
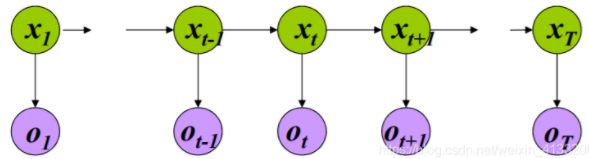
n时刻的观测值只依赖于n-1时刻的观测值,即:
p ( x n ∣ x n − 1 , x n − 2 , . . . x 0 ) = p ( x n ∣ x n − 1 ) p(x_n|x_{n-1},x_{n-2},...x_0) = p(x_n|x_{n-1}) p(xn∣xn−1,xn−2,...x0)=p(xn∣xn−1)
1.2 转移概率
a i , j = p ( x n = S j ∣ x n − 1 = S i ) a_{i,j} = p(x_n = S_j|x_{n-1} = S_i) ai,j=p(xn=Sj∣xn−1=Si)
1.3 时不变性
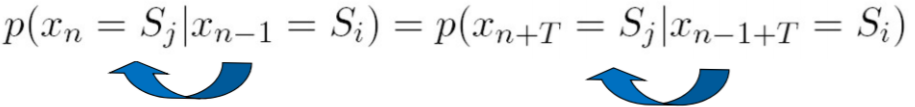
2.隐马尔科夫模型
2.1 引入问题
假设有一个人被锁在房间里待了很多天,但是他想知道外面的天气是什么。他猜测天气的唯一途径就是看每天来照顾他的人有没有带伞。
这样,观测状态(observed state)就是{带伞,不带伞}; 隐藏状态(hidden state)就是{晴,雨}。
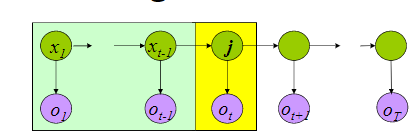
2.2 图像化表示

绿色圆圈是hidden state, 这是一个马尔可夫模型;
紫色圆圈是observed state, 只由对应的hidden state决定
2.3 形式化表示

- { S 1 , S 2 , . . . S N } \{S_1,S_2,...S_N\} { S1,S2,...SN}表示hidden states的状态
- { K 1 , K 2 , . . . K N } \{K_1,K_2,...K_N\} { K1,K2,...KN}表示observation的状态
- Π = { π i } \Pi=\{\pi_i\} Π={ πi}是初始状态的概率
- A = { a i , j } A=\{a_{i,j}\} A={ ai,j}是transition probability a i , j = p ( x n = j ∣ x n − 1 = i ) a_{i,j}=p(x_n=j |x_{n-1}=i) ai,j=p(xn=j∣xn−1=i)
- B = { b i , j } B=\{b_{i,j}\} B={ bi,j}是observation state probability b i , j = p ( y n = K j ∣ x n = S i ) b_{i,j}=p(y_n=K_j|x_n=S_i) bi,j=p(yn=Kj∣xn=Si)
2.4 HMM 能解决的问题
HMM的初始化模型 μ = { A , B , Π } \mu = \{A,B,\Pi\} μ={ A,B,Π} , 观测序列为 σ = { O 1 , O 2 , . . . O N } \sigma = \{O_1, O_2,...O_N\} σ={ O1,O2,...ON}
- 问题一(estimation problem):计算某个观测序列出现的概率
- 问题二(decoding problem):已知观测序列,求最有可能的hidden state
2.4.1 问题1(estimation problem)

2.4.1.1 Solution1
使用全概率公式,按照hidden states 拆分:
P ( O ∣ μ ) = ∑ X P ( O , X ∣ μ ) P(O|\mu) = \sum _{X} P(O,X|\mu) P(O∣μ)=X∑P(O,X∣μ)
其中, P ( O , X ∣ μ ) = P ( X ∣ μ ) P ( O ∣ X , μ ) P(O,X|\mu) = P(X|\mu)P(O | X, \mu) P(O,X∣μ)=P(X∣μ)P(O∣X,μ)

故: P ( O ∣ μ ) = ∑ X P ( X ∣ μ ) P ( O ∣ X , μ ) ( 1 ) P(O|\mu) = \sum _{X} P(X|\mu) P(O|X,\mu)~~~~(1) P(O∣μ)=X∑P(X∣μ)P(O∣X,μ) (1)
其中,
P ( X ∣ μ ) = π x 1 a x 1 x 2 a x 2 x 3 . . . a x T − 1 x T P(X|\mu) = \pi_{x_1}a_{x_1x_2}a_{x_2x_3}...a_{x_{T-1}x_T} P(X∣μ)=πx1ax1x2ax2x3...axT−1xT
这是因为 P ( X ∣ μ ) P(X|\mu) P(X∣μ)表示:在HMM 模型的初始条件下,hidden state为X的概率。
还有:
P ( O ∣ X , μ ) = b x 1 o 1 b x 2 o 2 . . . b x T o T P(O|X,\mu) = b_{x_1o_1}b_{x_2o_2}...b_{x_To_T} P(O∣X,μ)=bx1o1bx2o2...bxToT
这是因为 P ( O ∣ X , μ ) P(O|X,\mu) P(O∣X,μ)表示:在HMM模型的初始条件下,以及hidden states的条件下,观测值为O的概率。由于观测值只和hidden state有关,这里的 μ \mu μ 并没有作用。
这个算法的复杂度为 O ( 2 T N T ) O(2TN^T) O(2TNT), 其中T为序列长度,N为状态个数。
2.4.1.2 前向算法 (Forward Algorithm)
上面这种做法的明显不足就是复杂度太高了!前向算法通过动态规划来降低复杂度。
【算法1】前向算法
定义 α t ( i ) = p ( o 1 , . . . o t , x t = i ∣ μ ) , \alpha_t(i) = p(o_1,...o_t,x_t=i|\mu), αt(i)=p(o1,...ot,xt=i∣μ),则 P ( O ∣ μ ) = ∑ i = 1 N α T ( i ) P(O| \mu)= \sum _{i=1}^N \alpha_T(i) P(O∣μ)=∑i=1NαT(i)
又有:
α t + 1 ( j ) = p ( o 1 , . . . o t + 1 , x t + 1 = j ∣ μ ) = ∑ i = 1 N p ( o 1 , . . . o t + 1 , x t + 1 = j , x t = i ∣ μ ) ① = ∑ i = 1 N p ( o 1 , . . . o t + 1 , x t + 1 = j ∣ x t = i , μ ) p ( x t = i ∣ μ ) ② = ∑ i = 1 N p ( o 1 , . . . o t ∣ x t = i , μ ) p ( o t + 1 , x t + 1 = j ∣ x t = i , μ ) p ( x t = i ∣ μ ) ③ = ∑ i = 1 N p ( o 1 , . . . o t , x t = i ∣ μ ) p ( o t + 1 , x t + 1 = j ∣ x t = i , μ ) ④ = ∑ i = 1 N p ( o 1 , . . . o t , x t = i ∣ μ ) p ( x t + 1 = j ∣ x t = i , μ ) p ( o t + 1 ∣ x t + 1 = j ) ⑤ = ∑ i = 1 N α t ( i ) a i j b j o t + 1 \alpha_{t+1}(j)=p(o_1,...o_{t+1},x_{t+1}=j|\mu) \\=\sum _{i=1}^Np(o_1,...o_{t+1},x_{t+1}=j,x_t=i|\mu) ~~~①\\=\sum _{i=1}^Np(o_1,...o_{t+1},x_{t+1}=j|x_t=i,\mu)p(x_t=i|\mu)~~~~② \\= \sum _{i=1}^Np(o_1,...o_{t}|x_t=i,\mu)p(o_{t+1},x_{t+1}=j|x_t=i,\mu)p(x_t=i|\mu)③ \\=\sum _{i=1}^Np(o_1,...o_{t},x_t=i|\mu)p(o_{t+1},x_{t+1}=j|x_t=i,\mu)~~~④ \\=\sum _{i=1}^Np(o_1,...o_{t},x_t=i|\mu)p(x_{t+1}=j|x_t=i,\mu)p(o_{t+1}|x_{t+1}=j)~~~⑤ \\ = \sum_{i=1}^N \alpha_t(i)a_{ij}b_{j o_{t+1}} αt+1(j)=p(o1,...ot+1,xt+1=j∣μ)=i=1∑Np(o1,...ot+1,xt+1=j,xt=i∣μ) ①=i=1∑Np(o1,...ot+1,xt+1=j∣xt=i,μ)p(xt=i∣μ) ②=i=1∑Np(o1,...ot∣xt=i,μ)p(ot+1,xt+1=j∣xt=i,μ)p(xt=i∣μ)③=i=1∑Np(o1,...ot,xt=i∣μ)p(ot+1,xt+1=j∣xt=i,μ) ④=i=1∑Np(o1,...ot,xt=i∣μ)p(xt+1=j∣xt=i,μ)p(ot+1∣xt+1=j) ⑤=i=1∑Nαt(i)aijbjot+1
②->③:独立性假设
③->④: 第一项第三项合并
④->⑤: 第二项拆分
这样,有 α t + 1 ( j ) = ∑ i = 1 N α t ( i ) a i j b j o t + 1 \alpha_{t+1}(j) = \sum_{i=1}^N \alpha_t(i)a_{ij}b_{j o_{t+1}} αt+1(j)=∑i=1Nαt(i)aijbjot+1,又有 P ( O ∣ μ ) = ∑ i = 1 N α T ( i ) P(O| \mu)= \sum _{i=1}^N \alpha_T(i) P(O∣μ)=∑i=1NαT(i),于是复杂度为 O ( N 2 T ) O(N^2T) O(N2T)
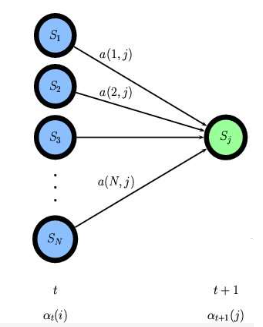
2.4.2 问题二(decoding problem)
解码问题就是,已知observed state, 求最有可能的hidden state,即
arg max X P ( X ∣ O ) \argmax_{X} P(X|O) XargmaxP(X∣O)
【算法2】viterbi 算法
令 δ t ( j ) = max x 1 , . . . x t − 1 p ( x 1 , . . . , x t − 1 , x t = j , o 1 , . . . o t ) \delta_t(j)= \max _{x_1,...x_{t-1}}p(x_1,...,x_{t-1},x_t=j,o_1,...o_t) δt(j)=x1,...xt−1maxp(x1,...,xt−1,xt=j,o1,...ot)
它代表了一个最大概率,如下图所示:
求 arg max X P ( X ∣ O ) \argmax_{X} P(X|O) XargmaxP(X∣O)等价于求 arg max X P ( X , O ) \argmax_{X} P(X,O) XargmaxP(X,O) 等价于求 arg max j δ T ( j ) \argmax_{j} \delta_T(j) jargmaxδT(j)
递推公式:
δ t + 1 ( j ) = max j δ t ( i ) a i j b j o t + 1 \delta_{t+1}(j) = \max_j \delta_t(i)a_{ij}b_{j o_{t+1}} δt+1(j)=jmaxδt(i)aijbjot+1
意思是,每个时刻的前一个时刻一定是概率最大的,在当前时刻也应该选择一个使概率最大的隐藏状态j。这样一步步把使得概率最大的隐藏状态记录下来,就是最后的结果。
2.5 HMM的应用
- 语音识别
- ★ \bigstar ★ 汉语拼音转汉字
(我大二的时候居然还写过这个,我可真厉害!要好好回忆一下细节…) - POS (part of speech) tagging