2019 南京ICPC网络赛 B super_log（幂塔函数求模、扩展欧拉降幂）

注：笔者是一名十八线蒟蒻 $ACMer$,因此文中可能有许多 $BUG$ ，请大佬们在评论区下留言，我会尽快改进。

原题

时间限制： $1000ms$，空间限制： $131072K$
In Complexity theory, some functions are nearly $O(1)$, but it is greater then $O(1)$. For example, the complexity of a typical disjoint set is $O(nα(n))$. Here $α(n)$ is Inverse Ackermann Function, which growth speed is very slow. So in practical application, we often assume $α(n)≤4$.

However $O(α(n))$ is greater than $O(1)$, that means if $n$ is large enough, $α(n)$ can greater than any constant value.

Now your task is let another slowly function $log^{*}x$ reach a constant value $b$. Here $log^{*}x$ is iterated logarithm function, it means “the number of times the logarithm function iteratively applied on $x$ before the result is less than logarithm base $a$”.
Formally, consider a iterated logarithm function $log^{*}x$

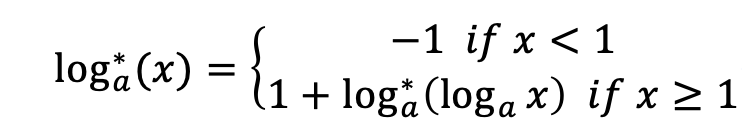
Find the minimum positive integer argument $x$, let $log^{*}_{a}x\geq b$ The answer may be very large, so just print the result $x$ after mod $m$.

Input
The first line of the input is a single integer $T(T≤300)$ indicating the number of test cases.

Each of the following lines contains $3$ integers $a$ , $b$ and $m$.

$1≤a≤1e6$
$0≤b≤1e6$
$1≤m≤1e6$
Note that if $a=1$, we consider the minimum number $x$ is $1$.
Output
For each test case, output $x$ mod $m$ in a single line.
Hint
In the $4−th$ query, $a=3$ and $b=2$. Then $log_{3}^* (27) = 1+ log_{3}^* (3) = 2 + log_{3}^* (1)=3+(-1)=2\geq b$, so the output is $27$ mod $16$ = $11$.
样例输入

5
2 0 3
3 1 2
3 1 100
3 2 16
5 3 233

样例输出

1
1
3
11
223

题面分析

总结起来就是：给出 $a,b,m$与 $log^{*}_{a}x$的计算方法，求最小的正整数 $x$，使得 $log^{*}_{a}x\geq b$ ， 输出 $x \ mod \ m。$ **
一般对于数学题，我们可以先试几个数来找找规律。
我们以 $a=2$为例，建议以下过程读者可以自己手推或者利用代码暴力打表。
当 $b=0$时， $x=1$。
当 $b=1$时，倒推回去可以得到 $x=2$。
同理， $b=2$时，得到 $x=4$。
$b=3$时， $x=16$。
$b=4$时， $x=65536$。
写到这里我们似乎看到了规律： $2$是 $2^{1}$， $4$是 $2^{2}$, $16$是 $2^{4}$, $65536$是 $2^{16}$，所以我们总结以下得到
答案是 $2^{2^{2^{2^{...^{2}}}}}_{_{_{共b个2}}}$。
那为了确认这个结论是否正确，我们再以 $a=3$为例，请读者试着自行推导。
当然我们同样可以得到答案是 $3^{3^{3^{3^{...^{3}}}}}_{_{共b个3}}$。
所以，我们可以假设：对于 $a,b,m$，答案为 $a^{a^{a^{a^{...^{a}}}}}_{_{_{共b个a}}} mod$ $m$。
数学题就是大胆猜想从不求证。但为了显得这篇博客很正经还是证明一下
证明：我们将 $a^{a^{a^{a^{...^{a}}}}}_{_{_{共b个a}}}$记为 $f(a,b)$，则
$log^{*}_{a}(f(a,b))$
$=1+log^{*}_{a}(f(a,b-1))$
$=2+log^{*}_{a}(f(a,b-2))$
$...$
$=b-1+log^{*}_{a}(f(a,1))$
$=b+log^{*}_{a}(a)$
$=b+1+log^{*}_{a}(1)$
$=b+1-1$
$=b$
于是该问题就转化为求这个幂塔函数 $a^{a^{a^{a^{...^{a}}}}}_{_{_{共b个a}}} mod$ $m$的结果。
因为 $1≤a≤1e6$， $0≤b≤1e6$， $1≤m≤1e6$，暴力算法直接超出范围，队友赛后用 $python$纯暴力算到超时，因此考虑新的策略。
我们可以先处理简单的情况： $a^b\ mod\ m,b$是个很大的数字，如果可以处理的话就可以递归解决问题。
这里就要请出本题的主角：欧拉降幂。

欧拉降幂

首先，我们有费马小定理 $a^{p-1}\equiv 1$ $(mod\ p),(gcd(a,p)=1)$。
又因为 $φ(p)=p-1(p∈prime)$，因此我们有 $a^{φ(p)}\equiv 1(mod \ p),(gcd(a,p)=1)$。
所以 $a^b\equiv a^{b\ modφ(p)}(mod p)$，我们称之为 欧拉降幂 。
但在本题中， $gcd(a,p)$不一定为 $1$，因此我们引入扩展欧拉降幂。

扩展欧拉降幂

首先我们给出结论

以下是证明，可以选择性跳过毕竟会用就行 。
当 $b<φ(p)$时易知。
当 $b\geq φ(p)$时证明如下：
（ 以下证明内容来自 scau_bi 的CN博客 https://www.cnblogs.com/bibibi/p/10269051.html）
首先我们证明一个引理。
引理：对于 $m$的一个质数因子 $p$，有
$p^c=p^{c\ mod φ(m)+φ(m)}(mod\ m)$
证：
我们设 $m=s*p^{r},gcd(s,p)=1$
有 $p^{φ(s)}\equiv1(mod$ $s),gcd(s,p)=1$(费马小定理)
因为 $φ(m)=φ(s)*φ(p^{r})$（ $φ$是积性函数，即 $φ(i)φ(j)=φ(i*j)$）
故 $p^{φ(m)}=p^{φ(s)^{φ(p^{r})}}\equiv 1^{φ(p^{r})}\equiv1(mod\ s)$
我们设 $p^{φ(m)}=k*s+1$
两边同乘 $p^r$，得
$p^{φ(m)+r}=k*s*p^r+p^r=k*m+p^r$
所以 $p^{φ(m)+r}\equiv p^r(mod\ m)$
于是我们可以把这个式子推广，得到
$p^{k*φ(m)+r}\equiv p^r(mod\ m)(k\geq 0)$--------------------（①）
又因为 $φ(m)$
$=φ(s)*φ(p^r)$
$\geqφ(p^r)$
$=(p-1)*p^{r-1}$(因为对于 $p^r$，除了 $p$的倍数以外都与其互质，因此 $φ(p^r)=p^r-p^{r-1}=(p-1)*p^{r-1}$)
$\geq r$
（这一步的证明：
$p=2$时可以用导数易得其成立。
$p>2$时 $(p-1)*p^{r-1}\geq (p-1)*e^{r-1}\geq(p-1)*(r-1+1)=(p-1)*r\geq r$。
这里利用了 $e^x\geq x+1这个性质$,因为 $x+1$是 $e^x在(0,1)的切线方程$ ）
因此 $p^c(c \geq r)$
$\equiv p^{c-r+r}(mod\ m)$
$\equiv p^{c-r}*p^r(mod\ m)$
$\equiv p^{c-r}*p^{r+φ(m)}(mod\ m)$
$\equiv p^{c+φ(m)}(mod\ m)(c \geq r)$
因为 $c\geq r,r\geq φ(m)$，故 $c\geqφ(m)$
那我们利用①式得到
$p^{c+φ(m)}\equiv p^{c\ modφ(m)+φ(m)}(mod\ m),c\geq φ(m)$--------------------（②）
而对于 $p^{k^c}$，我们也可以通过②式有
$p^{k^c}\equiv p^{kc}\equiv p^{φ(m)+kc}\equiv (p^k)^{c+φ(m)}\equiv (p^k)^{c\ modφ(m)+φ(m)}(mod\ m)$
因此，我们把一个任意数 $a$拆成 $p_{1}^{a_{1}}p_{2}^{a_{2}}...p_{k}^{a_{k}}$，则相乘后可以得到
$a^c\equiv a^{c\ modφ(m)+φ(m)}(mod\ m),(c\geqφ(m))$
终于证毕。建议想学懂原理的读者自行手推一遍！
好，有了解决的办法，我们就考虑递归写一个函数 $f(b,p)$， $b$为递归的层数， $p$是当前的模数。
每一次都利用快速幂实现 $a^{f(b-1,φ(p))}(mod\ p)$的调用。到最后一层返回 $a$或者 $a\ mod\ φ(p)+φ(p)$。
注意在回溯时快速幂的结果也要根据扩展欧拉降幂进行改变！

AC代码（4ms）

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
long long a,b,m;
long long phi(long long n)
{
    long long ans = n;
    for(int i = 2; i*i <= n; i++)
    {
        if(n % i == 0)
        {
            ans -= ans/i; //等价于通项，把n乘进去
            while(n % i == 0) //确保下一个i是n的素因数
                n /= i;
        }
    }
    if(n > 1)ans -= ans/n; //最后可能还剩下一个素因数没有除
    return ans;
}
long long MOD(long long a,long long mm)//扩展欧几里得的结果
{
	return a>=mm？a%(mm)+(mm):a;
}
long long qsm(long long a,long long b,long long c)//快速幂
{
	if(!c)
		return 0;
    long long ans=1,base=a;
    while(b!=0)
	{
        if(b&1)
        ans=MOD(ans*base,c);
        base=MOD(base*base,c);//注意这两行！回溯时也要根据扩展欧拉降幂！
        b>>=1;
	}
	return MOD(ans,c);//答案也要！
}
long long f(long long b,long long mm)
{
	if(mm==1)
		return MOD(a,1);//模数为1时停止计算，因为之后的结果都是相同的
	if(b==1)
	{
		return MOD(a,mm);//最后一层的情况
	}
	return qsm(a,f(b-1,phi(mm)),mm);//递归调用
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%lld%lld%lld",&a,&b,&m);
		if(b==0 || a==1 || m==1)//特殊情况直接输出
		{
			printf("%lld\n",1%m);
			continue;
		}
		if(b==1)//特殊情况直接输出
		{
			printf("%lld\n",a%m);
			continue;
		}
		long long ans=f(b,m)%m;
		printf("%lld\n",ans);
	}
}

后记

昨天比赛时没能想到快速幂回溯，然后就是无尽的WA…，主要还是菜。
除了从外到内的递归法外，这题其实还可以从内到外来做，不容易错，有兴趣的读者可以尝试。
当然，这题也可以推广到更一般的问题：求 $x_1^{x_2^{...^{x_n}}}mod\ m$,只要将上面的代码微调即可。
最后的最后，感谢一波赛后蔡队一针见血的指点。CSLNB!
DrGilbert 2019.9.2