super_log （广义欧拉降幂）（2019南京网络赛）

题目：

In Complexity theory, some functions are nearly $\le 4α(n)≤4.$

However

Now your task is let another slowly function

Formally, consider a iterated logarithm function $^*loga∗$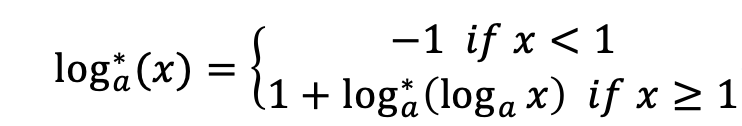

Find the minimum positive integer argument $log_{a}^* (x) \ge bloga∗(x)≥b. The answer may be very large, so just print the result xx after mod mm.$

Input

The first line of the input is a single integer $T(T\le 300)T(T≤300) indicating the number of test cases.$

Each of the following lines contains

$\le a \le 10000001≤a≤1000000$

$\le b \le 10000000≤b≤1000000$

$\le m \le 10000001≤m≤1000000$

Note that if a==1, we consider the minimum number x is 1.

Output

For each test case, output

Hint

In the $log_{3}^* (27) = 1+ log_{3}^* (3) = 2 + log_{3}^* (1)=3+(-1)=2 \ge blog3∗(27)=1+log3∗(3)=2+log3∗(1)=3+(−1)=2≥b, so the output is 2727 mod 16 = 1116=11.$

样例输入

样例输出

1
1
3
11
223

解题报告：严重怀疑这场比赛的出题方，读题实在是太困难了，看了半个小时才理解了要求解什么东西，一看就是一个广义欧拉降幂，然后就直接去写的之前的模板，求解无穷个2的幂次，
但是修修改改的过了样例，但是忘记了广义欧拉降幂的实现，疯狂wa，在比赛结束后找了好久才发现是没有去使用广义欧拉降幂的性质，忘记在该加欧拉（m）的地方进行加了，隔壁队的
数论手，给了一个能够实现这个功能的快速幂，稍微一修改就A了。这个需要掌握了，当时时间太紧，头脑已经混了。

ac代码：

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<cmath>
 5 #include<algorithm>
 6 #include<map>
 7 #include<vector>
 8 using namespace std;
 9 typedef long long ll;
10 
11 const int maxn=1e7+10;
12 vector<int> prime;
13 int phi[maxn];
14 
15 void db_Onion()
16 {
17     phi[1]=1;
18     for(int i=2;i<maxn;i++)
19     {
20         if(phi[i]==0)
21         {
22             prime.push_back(i);
23             phi[i]=i-1;
24         }
25         for(int j=0;j<prime.size()&&prime[j]*i<maxn;j++)
26         {
27             if(i%prime[j]==0)
28             {
29                 phi[i*prime[j]]=phi[i]*prime[j];
30                 break;
31             }
32             else
33             {
34                 phi[i*prime[j]]=phi[i]*(prime[j]-1);
35             }
36         }
37     }
38 }
39 ll a,b,m;
40 ll cal(ll x,ll m)
41 {
42     if(x<m)
43         return x;
44     else
45         return x%m+m;
46 }
47 
48 ll ans;
49 
50 ll ksm(ll r,ll n,ll m)
51 {
52     ll d=r,ans=1;
53     bool f=0;
54     if(r==0&&n==0)return 1;
55     while(n){
56         if(n&1){
57             ans=ans*d;
58             if(ans>=m){
59                 ans%=m;f=1;
60             }
61         }
62         d=d*d;
63         if(n>1&&d>=m){
64             d%=m;f=1;
65         }
66         n>>=1;
67     }
68     if(f)ans+=m;
69     return ans;
70 }
71 ll slove(ll p,int tot)
72 {
73     if(tot==b+1)
74         return 1;
75     if(p==1)
76         return 1;
77     
78     ll tmp=slove(phi[p],tot+1); 
79     return ksm(a,tmp,p);        
80 }
81 
82 int main()
83 {
84     db_Onion();
85     int t;
86     scanf("%d",&t);
87     while(t--)
88     {
89         scanf("%lld%lld%lld",&a,&b,&m);
90         if(b==0||a==1)
91         {
92             printf("%lld\n",1%m);
93             continue;
94         }
95         ans=0;
96         printf("%lld\n",slove(m,1)%m);
97     }
98 }