一、多阶段决策过程的最优化问题
在现实生活中,有类活 动的过程,由于 它的特殊性,可将过程分成若干个互相阶段。在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。当阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展,当段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线,这个问题看作是个前后关联具有链状结构的 多阶段过程就称为多阶段决策过程,这就称为多阶段决策问题。
多阶段决策过程,是指这样的一类特殊的活动过程,问题可以按时间顺序分解互联系的阶段,在每-个阶段都要作出决策,全部过程的决策是-个决策序列。
二、能采用动态规划求解的问题的一般要具有3个性质:
最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只 与当前状态有关。
有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
三、动态规划基本概念
状态:描述事物的性质,不同事物有不同的性质,因而用不同的状态来刻画。对问题的求解状态的描述是分阶段的。
决策:根据题意要求,对每个阶段所做出的某种选择性操作。
状态转移方程:用数学公式描述与阶段相关的状态间的演变规律。
四、解题步骤:
- 拆分问题
- 定义状态(并找出初状态)
- 状态转移方程
五、模型方法
第一种递归搜索法。
第二种递归搜索法+记忆。
第三种递推式法。
六、例题
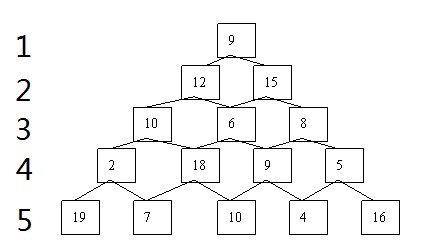
数塔问题
思路分析:
贪心不可解,每一步都会影响后续的操作。
在用动态规划考虑数塔问题时可以自顶向下的分析,自底向上的计算。
从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值,只要左右两道路径上的最大值求出来了才能作出决策。同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去,直到倒数第二层时就非常明了。
所以第一步对第五层的8个数据,做如下四次决策:
如果经过第四层2,则在第五层的19和7中肯定是19;
如果经过第四层18,则在第五层的7和10中肯定是10;
如果经过第四层9,则在第五层的10和4中肯定是10;
如果经过第四层5,则在第五层的4和16中肯定是16;
经过一次决策,问题降了一阶。5层数塔问题转换成4层数塔问题,如此循环决策…… 最后得到1阶的数塔问题。
#include <bits/stdc++.h
using namespace std;
const int MAXN = 100+10;
int num[MAXN][MAXN];
int dp[MAXN][MAXN];
int main()
{
int t;
scanf("%d", &t);
while( t-- )
{
memset(dp, 0, sizeof(dp));
int n;
scanf("%d", &n);
for( int i=1; i<=n; i++ )
{
for( int j=1; j<=i; j++ )
scanf("%d", &num[i][j]);
}
for( int j=1; j<=n; j++ )
dp[n][j] = num[n][j];
for( int i = n-1; i = 1; i-- )
{
for( int j=1; j <= i; j++ )
{
dp[i][j] = num[i][j] + max(dp[i+1][j], dp[i+1][j+1]);
}
}
printf("%d\n", dp[1][1] );
}
return 0;
}
1.以上篇文章数塔为例
上一章用的是递归的做法,这次我们采用递推的做法。
递归:从已知问题的结果出发,用迭代表达式逐步推算出问题的开始的条件,即顺推法的逆过程,称为递归。
递推:递推算法是一种用若干步可重复运算来描述复杂问题的方法。递推是序列计算中的一种常用算法。通常是通过计算机前面的一些项来得出序列中的指定象的值。
递归与递推区别:相对于递归算法,递推算法免除了数据进出栈的过程,也就是说,不需要函数不断的向边界值靠拢,而直接从边界出发,直到求出函数值。
斐波那契数列:已知f(1) = 1 , f(2) = 1 , 且满足关系式f(n) = f(n-1) + f(n-2),则f(50)等于多少?
分析:根据初始条件f(1) = 1 , f(2) = 1 和关系式f(n) = f(n-1) + f(n-2),可知,f(3) = f(2) + f(1) , f(3) = f(2) + f(1) …….
编写代码(递归)
第四层的取值等于左下或者右下与自己的加和,第四层就有max{2+19,2+7} max{18+7,18+10} max{9+10,9+4} max{5+4,5+16}
结果第四层就变成了 21,28,19,21。这样五层变成了四层。以此类推n层变为n-1层到1层。更易求出最大值。
代码实现过程如下
#include<bits/stdc++.h
using namespace std;
int main
{
int ob[10][10];
int temp;
cinN;//数塔层数
for(int i=0;i<N;i++)
{
for(t=0;t<=i;t++)
{
cina[i][j];
}
}
for(int i=N-1;i=1;i--)
{
for(int t=0;t<=i;t++)
{
temp=max{a[i+1][t],a[i+1][t+1];
a[i][t]=a[i][t]+temp;
}
}
1、线性模型
线性模型的是动态规划中最常用的模型,上文讲到的最长单调子序列就是经典的线性模型,这里的线性指的是状态的排布是性的。
2、区间模型
区间模型的状态表示一般为d[i][j],表示区间[i, j]上的最优解,然后通过状态转移计算出[i+1, j]或者[i, j+1]上的最优解,逐步扩大区间的范围,最终求得[1, len]的最优解。
3、背包模型
背包问题是动态规划中一个最典型的问题之一。由于网上有非常详尽的背包讲解,这里只将常用部分抽出来,具体推导过程详见 《背包九讲》。
a.0/1背包
有N种物品(每种物品1件)和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci,得到 的价值是Wi。求解将哪些物品装入背包可使价值总和最大。
f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。
决策为第i个物品在前i-1个物品放置完毕后,是选择放还是不放,状态转移方程为:
f[i][v] = max{ f[i-1][v], f[i-1][v - Ci] +Wi }
时间复杂度O(VN),空间复杂度O(VN) (空间复杂度可利用滚动数组进行优化达到O(V),下文会介绍滚动数组优化)。
b.完全背包
有N种物品(每种物品无限件)和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci,得到 的价值是Wi。求解将哪些物品装入背包可使价值总和最大。
f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。
f[i][v] = max{ f[i-1][v - kCi] + kWi | 0 <= k <= v/Ci } (当k的取值为0,1时,这就是01背包的状态转移方程)
时间复杂度O( VNsum{V/Ci} ),空间复杂度在用滚动数组优化后可以达到 O( V )。
进行优化后(此处省略500字),状态转移方程变成:
f[i][v] = max{ f[i-1][v], f[i][v - Ci] +Wi }
时间复杂度降为 O(VN)。
c.多重背包
有N种物品(每种物品Mi件)和一个容量为V的背包。放入第i种物品耗费的空间是Ci,得到 的价值是Wi。求解将哪些物品装入背包可使价值总和最大。
f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。
f[i][v] = max{ f[i-1][v - kCi] + kWi | 0 <= k <= Mi }
时间复杂度O( Vsum(Mi) ), 空间复杂度仍然可以用滚动数组优化后可以达到 O( V )。
优化:采用二进制拆分物品,将Mi个物品拆分成容量为1、2、4、8、... 2^k、Mi-( 2^(k+1) - 1 ) 个对应价值为Wi、2Wi、4Wi、8Wi、...、2^kWi、( Mi-( 2^(k+1) - 1 )
)Wi的物品,然后采用01背包求解。 这样做的时间复杂度降为O(Vsum(logMi) )。找不到出处了
给定一个字符串s,你可以从中删除一些字符,使得剩下的串是一个回文串。如何删除才能使得回文串最长呢? 输出需要删除的字符个数。
本题可转化为动态规划算法求解最长公共子序列问题,然后用总字符串长度减去最长子序列长度,便得出问题的答案。
先将给定的初始字符串S1反过来排列,设为S2,求S1和S2的最长公共子序列便可。C++代码如下:
#include <iostream
#include <string
#include <algorithm
using namespace std;
int temp[100][100];
void caculate(string s1){
string s2(s1);
reverse(s2.begin(), s2.end());
int len = s1.length();
memset(temp, 0, sizeof(temp));
for (int i = 0; i<len; ++i)
{
for (int j = 0; j<len; ++j)
{
if (s1[i] == s2[j])
temp[i + 1][j + 1] = temp[i][j] + 1;
else
temp[i + 1][j + 1] = max(temp[i][j + 1], temp[i + 1][j]);
}
}
cout << len - temp[len][len] << endl;
}
int main()
{
string s;
getline(cin, s);
caculate(s);
system("pause");
return 0;
}
相关题目:
简单基础dp
hdu 2084 数塔 简单从上往下递推
hdu 2018 母牛的故事 简单递推计数
hdu 2044 一只小蜜蜂… 简单递推计数(Fibonacci)
hdu 2041 超级楼梯 Fibonacci
hdu 2050 折线分割平面 找递推公式
CF 429B B.Working out 四个角递推
zoj 3747 Attack on Titans 带限制条件的计数递推dp
uva 10328 Coin Toss 同上题
hdu 4747 Mex
hdu 4489 The King’s Ups and Downs
hdu 4054 Number String
背包
hdu 2955 Robberies 01背包
hdu 1864 最大报销额 01背包
hdu 2602 Bone Collector 01背包
hdu 2844 Coins 多重背包
hdu 2159 FATE 完全背包
woj 1537 A Stone-I 转化成背包
woj 1538 B Stone-II 转化成背包
poj 1170 Shopping Offers 状压+背包
zoj 3769 Diablo III 带限制条件的背包
zoj 3638 Fruit Ninja 背包的转化成组合数学
hdu 3092 Least common multiple 转化成完全背包问题
poj 1015 Jury Compromise 扩大区间+输出路径
poj 1112 Team Them UP 图论+背包
LIS
hdu 1003 Max Sum
hdu 1087 Super Jumping!
uva 10635 Prince and Princess LCS转化成LIS
hdu 4352 XHXJ’s LIS 数位dp+LIS思想
srm div2 1000 状态压缩+LIS
poj 1239 Increasing Sequence 两次dp
LCS
hdu 1503 Advanced Fruits
hdu 1159 Common Subsequence
uva 111 History Grading
poj 1080 Human Gene Functions
区间dp
poj 1141 Brackets Sequence 括号匹配并输出方案
hdu 4745 Two Rabbits 转化成求回文串
zoj 3541 The Last Puzzle 贪心+区间dp
poj 2955 Brackets
hdu 4283 You Are the One 常见写法
hdu 2476 String Printer
zoj 3537 Cake
CF 149D Coloring Brackets
zoj 3469 Food Delivery
树形dp
hdu 4123 Bob’s Race 二分+树形dp+单调队列
hdu 4514 求树的直径
poj 1655 Balancing Act
hdu 4714 Tree2Cycle 思维
hdu 4616 Game
hdu 4126 Genghis Kehan the Conqueror MST+树形dp 比较经典
hdu 4756 Install Air Conditioning MST+树形dp 同上
hdu 3660 Alice and Bob’s Trip 有点像对抗搜索
CF 337D Book of Evil 树直径的思想 思维
hdu 2196 Computer 搜两遍
数位dp
hdu 2089 不要62 简单数位dp
hdu 3709 Balanced Number 比较简单
CF 401D Roman and Numbers 状压+数位dp
hdu 4398 X mod f(x) 把模数加进状态里面
hdu 4734 F(x) 简单数位dp
hdu 3693 Math teacher’s homework 思维变换的数位dp
hdu 4352 XHXJ’s LIS 数位dp+LIS思想
CF 55D Beautiful Numbers 比较巧妙的数位dp
hdu 3565 Bi-peak Numbers 比较难想
CF 258B Little Elephant and Elections 数位dp+组合数学+逆元
概率(期望) dp
ural 1776 Anniversiry Firework 比较基础
hdu 4418 Time travel 比较经典BFS+概率dp+高斯消元
hdu 4586 Play the Dice 推公式比较水
hdu 4487 Maximum Random Walk
jobdu 1546 迷宫问题 高斯消元+概率dp+BFS预处理
hdu 3853 LOOPS 简单概率dp
hdu 4405 Aeroplane chess 简单概率dp,比较直接
hdu 4089 Activation 比较经典
poj 2096 Collecting Bugs 题目比较难读懂
zoj 3640 Help me Escape 从后往前,比较简单
hdu 4034 Maze 经典好题,借助树的概率dp
hdu 4336 Card Collector 状态压缩+概率dp
hdu 4326 Game 这个题状态有点难抽象
状态压缩dp
这类问题有TSP、插头dp(轮廓线DP)等。
hdu 1693 Eat the Trees 插头dp
hdu 4568 Hunter 最短路+TSP
hdu 4539 插头dp
hdu 4529 状压dp
poj 1185 炮兵阵地
poj 2411 Mandriann’s Dream 轮廓线dp
hdu 3811 Permutation
poj 1038
poj 2441
hdu 2167
hdu 4026
hdu 4281